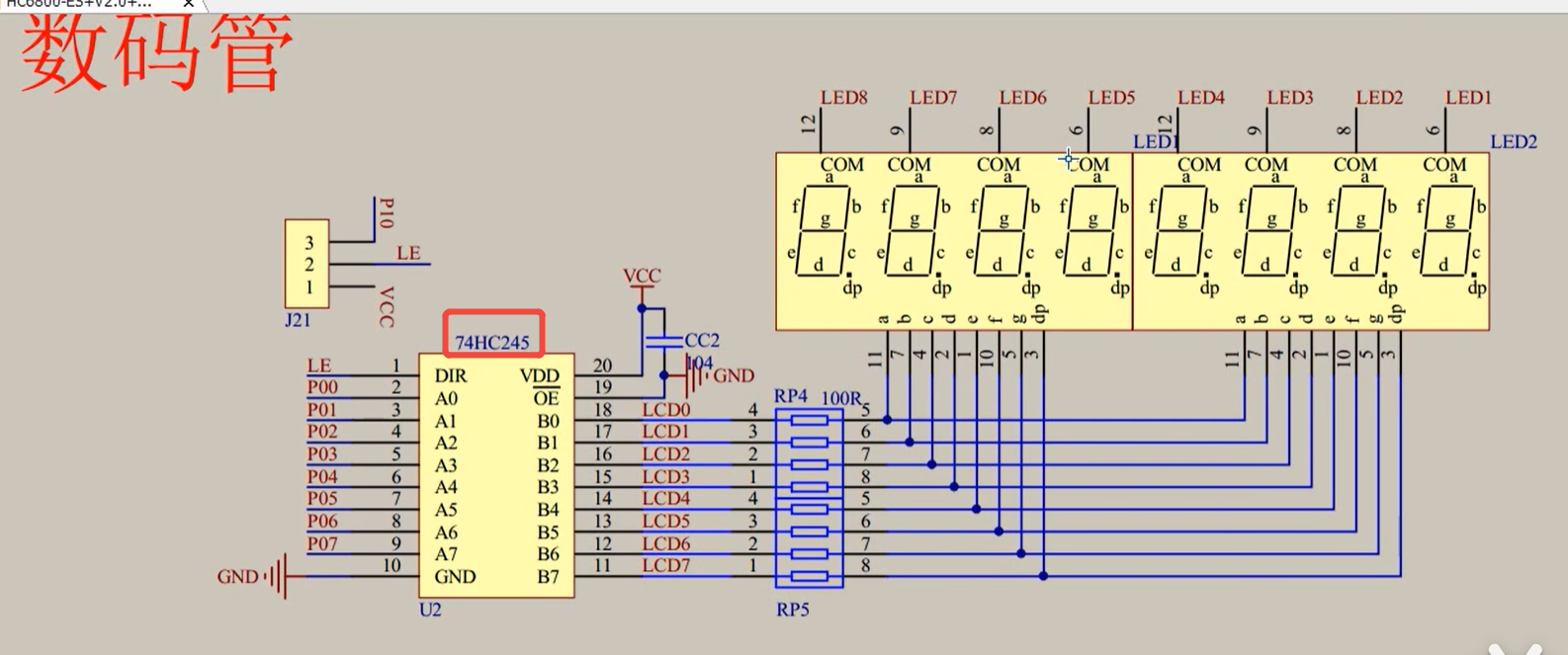
优化算法——SGD、Momentum、Adagrad、RMSprop、Adam、AdamW
- 统一数学表达:设损失函数为$\mathcal{L}(\theta) $,学习率为$\eta$。
- 每次迭代仅使用一个随机小批量(mini-batch)数据计算梯度。
- 从训练集中采样包含小批量$m$个样本${x{(1)},\cdots,x{(m)}}$,其对应的目标为${y{(1)},\cdots,y{(m)}}$。则用于计算的梯度$\displaystyle g=\frac{1}{m}\sum_{i=1}^m\nabla_\theta \mathcal{L} (f(x{(i)};\theta),y)$。
- 本文中出现的数学表达式中的参数是单个元素,当参数为矩阵时,对矩阵中的每个元素进行相同的更新操作。比如$g$是矩阵,则$g^2=g\odot g$。
1. SGD
1.1 基本概念
-
随机梯度下降,stochastic gradient descent。
-
更新公式$\theta_{t+1}\leftarrow\theta_t-\eta\cdot g$。
-
PyTorch中调用方法
# (params: _params_t, lr: float, momentum: float = ..., dampening: float = ..., weight_decay: float = ..., nesterov: bool = ...) -> Noneoptimizer = torch.optim.SGD(model.parameters(), lr=learning_rate)
1.2 Case study
- 更新不稳定
- 设$J(x,y)=x2+9y2$,初始$(x_0,y_0)=(2,2)$,设置学习率$\eta=0.1$。假设用mini-batch求出来的梯度就是理论值,则更新公式为$(x,y)=(x-\eta\nabla_xJ,y-\eta\nabla_yJ)=(0.8x,-0.8y)$。根据SGD优化到最低点$(0,0)$:$(2,2)\rightarrow(1.6,-1.6)\rightarrow(1.28,1.28)\rightarrow(1.024,-1.024)\rightarrow\cdots$。由此看出梯度大时导致收敛不稳定,产生震荡。
2 Momentum
- 动量法
optimizer = torch.optim.SGD(model.parameters(), lr=learning_rate, momentum=0.9)
2.1 指数加权平均
| day | 观测值$\theta$ | 代替$\theta$的估计值$v$ |
|---|---|---|
| 1 | 100 | 30 |
| 2 | 107 | 53.1 |
| 3 | 105 | 68.67 |
| 4 | 110 | 81.069 |
| 5 | 126 | 94.5483 |
| 6 | 120 | 102.18381 |
| 7 | 130 | ? |
-
有什么用:刻画数据变化的趋势。比如上述表格中观测值虽然不是单调递增的,但其整体的趋势是增长的,因此用$v$来刻画该增长趋势。
-
现在希望预测第7天的值,可以想到用加权平均$\displaystyle v_7=\frac{1}{7}\sum_{i=1}^{7}\theta_i$。但实际上越近期的数据权重应该更大,因此用指数加权平均:$v_t=\beta v_{t-1}+(1-\beta)\theta_t$。
-
初始$v_0=0,\beta=0.7$。填入表格。可以发现当时间序列较短时,最早几天的$v$值很小,不准确。时间序列够长,$v_0$的权重越小,即影响越小。
-
修正:$\displaystyle v_t{correct}=\frac{v_t}{1-\betat}$。
2.2 基本概念
- 引入历史梯度加权平均,在梯度方向一致时加速收敛,减少SGD中的震荡,从而更加稳定。
- 数学表示:
- 速度更新(累计梯度):$v_t=\gamma v_{t-1}+(1-\gamma)\cdot g$。其中$\gamma$为动量系数,一般设置为0.9。
- 参数更新:$\theta_t=\theta_{t-1}-\eta\cdot v_t$。
3 Adagrad
-
Adaptive Gradient Algorithm。自适应学习率优化算法,根据参数的历史梯度动态调整学习率,尤其适用于稀疏数据和高维优化问题。
-
数学表达:
- 累计梯度平方和:$G=G+g^2$。初始化$G=0$。
- 参数更新:$\displaystyle \theta_{t+1}=\theta_t-\frac{\eta}{\sqrt{G+\varepsilon}}\cdot g$。其中$\eta$是全局学习率(超参数),$\varepsilon$是防止除0的很小的数。
-
问题:累计越来越大,导致后期收敛缓慢。
3.1 优化:RMSprop
- Root Mean Square Propagation。
- PyTorch调用:
optimizer = torch.optim.RMSprop(model.parameters(), lr=0.01, momentum=0.9)
- 与Adagrad唯一不同的地方:
- 累计梯度平方换成了指数加权平均:$G=\beta\cdot G+(1-\beta)\cdot g^2$。
- 但后期容易在小范围内产生震荡。
4 ✅Adam
- Adam = RMSprop + Momentum。对学习率(步长)不敏感,建议默认0.001。
- $s,r$初始化均为0;$\beta_1=0.9,\beta_2=0.999$。数学表达:
- 一阶矩估计(Monmentum部分):$s=\beta_1s+(1-\beta_1)\cdot g$。
- 二阶矩估计(RMSprop部分):$r=\beta_2r+(1-\beta_2)\cdot g^2$。
- 修正:$\displaystyle\hat{s}=\frac{s}{1-\beta_1t},\hat{r}=\frac{r}{1-\beta_2t}$。
- 更新:$\displaystyle \theta\leftarrow\theta-\frac{\eta}{\sqrt{\hat{r}}+\varepsilon}\hat{s}$。
- PyTorch调用:
optimizer = torch.optim.Adam(params, lr=learning_rate, weight_decay=weight_decay)
4.1 AdamW
- W:weight decay,权重衰减系数$\lambda$。达到泛化。
- 不是L2正则化(L2 Regularization):$\displaystyle \mathcal{L}=\mathcal{L}(\theta)+\frac{\lambda}{2}\left | \theta \right |^2$。因为修改了损失函数。
- 唯一不同:$\theta\leftarrow\theta-\frac{\eta}{\sqrt{\hat{r}}+\varepsilon}\hat{s}-{\color{Red} \lambda\cdot \eta\theta} $。