1.基本概念
T检验 是一种统计学方法,用于判断两组数据的均值是否存在显著差异 。其核心思想是通过计算“t值”和对应的“p值”,评估观察到的差异是否由随机误差引起,还是反映了真实的生物学或实验效应。
适用场景 :
- 比较两组独立样本的均值(如对照组 vs 实验组)。
- 检验单组数据的均值是否与已知理论值不同。
- 分析配对数据的差异(如同一批样本处理前后的测量值。
2.T检验的类型
根据数据特性和实验设计,T检验分为三种:
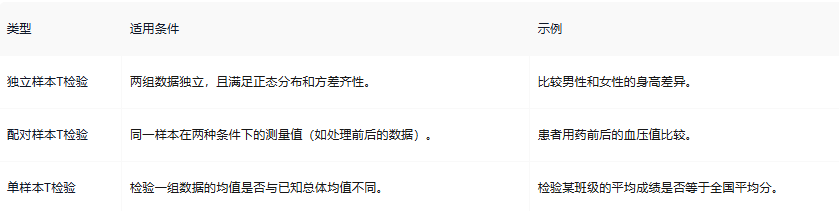
3.T检验的假设条件
在使用T检验前需验证以下前提:
- 正态性 :数据近似服从正态分布(可通过Q-Q图、Shapiro-Wilk检验判断)。
- 方差齐性 (仅独立样本T检验):两组数据的方差无显著差异(通过Levene检验或F检验判断)。
- 独立性 :样本间相互独立(如不同组别样本无关联)。
注 :若数据不满足正态性或方差齐性,可改用非参数检验(如Mann-Whitney U检验)。
4. T检验的计算步骤

5.结果解读
- p值
- 若\(p<\alpha\)(通常取为0.05),拒绝原假设(两组均值无差异),认为差异显著;
- 若\(p>=\alpha\),不能拒绝原假设,差异不显著。
- 效应值
衡量差异的实际意义(如Cohen's d),避免仅依赖\(p\)值;- d=0.2(小效应),d=0.5(中效应),d=0.8(大效应)
6. 应用场景示例
生物学实验 :
- 比较基因A在癌症组织和正常组织中的表达量(独立样本T检验)。
- 分析药物处理前后小鼠体重的差异(配对样本T检验)。
注意事项 : - 多重检验问题 :若同时进行多次T检验(如高通量数据分析),需校正p值(如Bonferroni校正)。
- 样本量影响 :小样本可能导致检验效能不足(无法检测到真实差异)。
6.与方差分析(ANOVA)的区别
- T检验 :仅适用于两组比较。
- ANOVA :用于三组及以上均值比较,后续需结合post hoc检验(如Tukey HSD)。
7. Wilcoxon and Kruskal-Wallis tests
当数据不满足正态分布或方差齐性 时,参数检验(如T检验、ANOVA)的可靠性下降。此时,非参数检验 通过分析数据的秩次(Rank)而非原始值,提供更稳健的统计推断。
Wilcoxon检验 :用于两组比较(配对或独立样本)。
Kruskal-Wallis检验 :用于三组及以上独立样本的比较(非参数版ANOVA)。
Wilcoxon检验
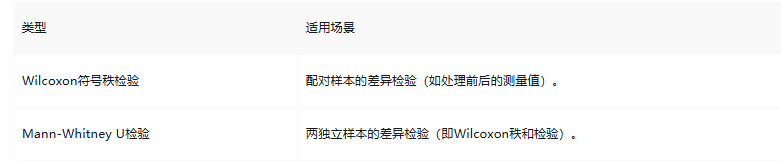

Kruskal-Wallis检验
用于比较三组及以上独立样本的中位数差异(非参数版ANOVA)

与参数检验的对比

5. 参数检验和非参数检验的区别
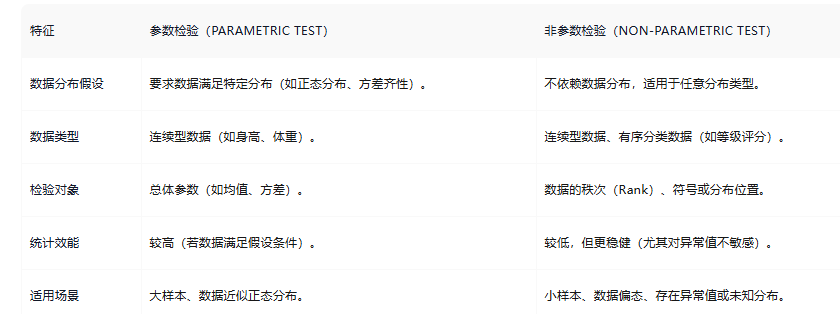
- 参数检验(Parametric Test)
- "参数”指总体分布的特征值(如正态分布的均值\(\mu\),方差\(\sigma^2\))
- 检验基于对总体参数的假设(例如t检验假设两组数据来自正态分布总体,比较均值差异)
- 使用参数检验的条件:
- 数据近似正态分布(可通过QQ图,Shapiro-Wilk检验判断)
- 方差齐性(如独立样本T检验需Levene检验验证)
- 数据为连续型变量且无显著异常值
- 非参数检验(Non-parametric Test)
- 不依赖总体分布的参数,仅关注数据的秩次或顺序关系。
- 例如,Mann-Whitney U检验比较两组数据的秩和,而非原始数值。
- 使用非参数检验的条件:
- 数据严重偏态或分布未知
- 存在极端异常值或数据为有序分类变量
- 小样本(如n<30)且无法验证正态性