选与不选问题中的暂时答案假定思想

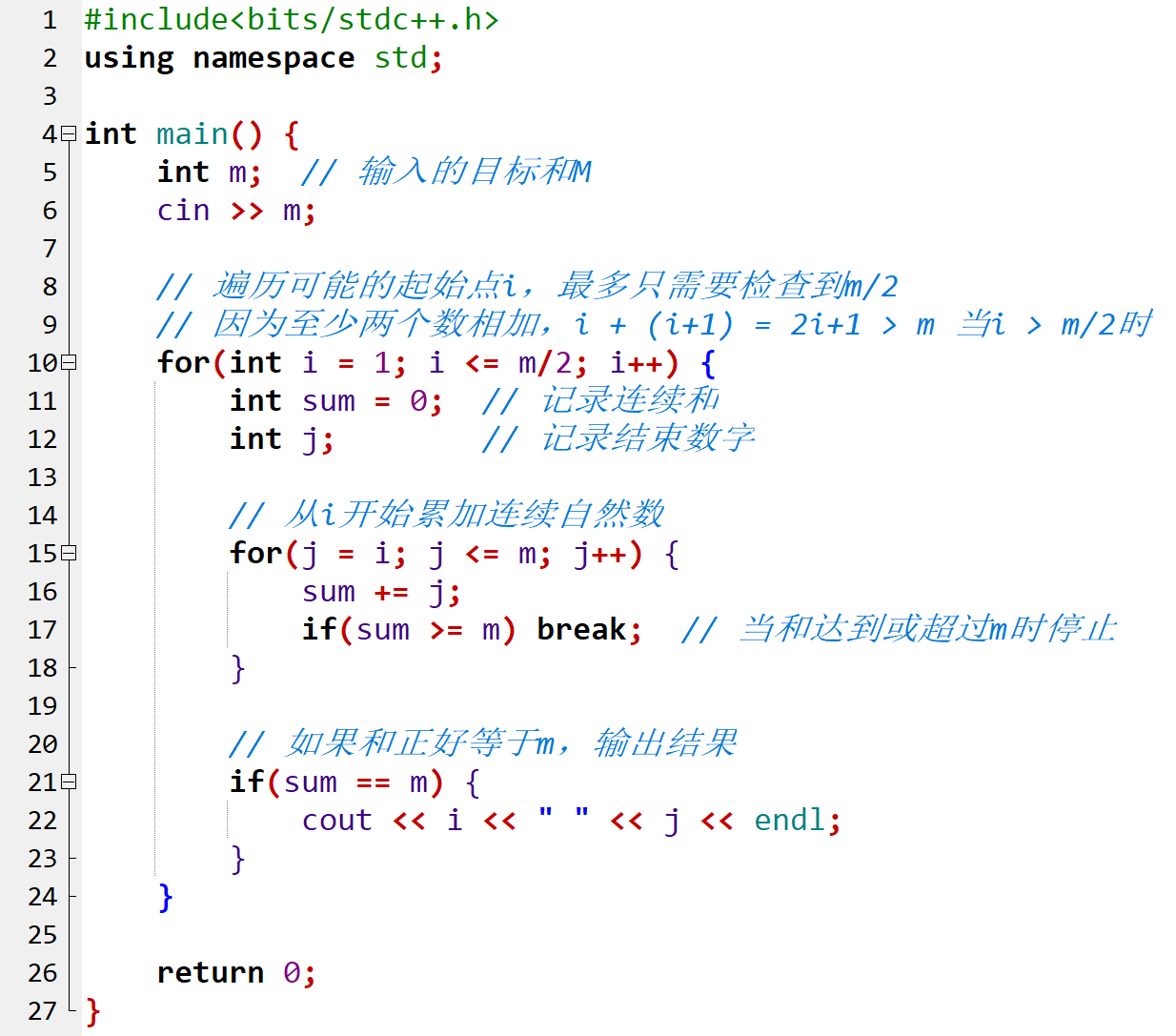
你有一个长度为 n 的数组 a ，由 n 个非零整数组成。最初，你有 0 枚硬币，你将进行以下操作，直到 a 为空：

• 假设m是a的当前大小。选择一个整数 i , 其中1≤i≤m,获得|ai| 枚金币，这里的 |ai|表示 ai 的绝对值, 然后：
  • 如果是 ai<0，则用 [a1,a2,…,ai−1][a1,a2,…,ai−1] 替换 a (即删除以 ai 开头的后缀)；
  • 否则，将 a 替换为 [ai+1,ai+2,…,am][ai+1,ai+2,…,am] (即删除以 ai 结尾的前缀)。

求过程结束时硬币的最大数量。

分析

有一些题不是用来模拟的,是用来假定答案的

这里引用一下cf的官方题解

首先我们可以看到，在任何时候，我们要么删除最左边的正数元素，要么删除最右边的负数元素，因为如果我们删除的不是最左边的正数元素，那么我们就可以先删除最左边的正数元素，从而获得更高的分数，而删除最右边的负数元素也有类似的道理。因此，要计算答案，我们只需检查将数组分成(正数)前缀和还有(负数)后缀(和)的所有 n+1 方法，并取其中的最大值，这在 O(n) 中很容易做到。

通过分析题意, 注意到 :

选正数-> 删前缀

选负数-> 删后缀

在选一个正数之前, 最优的解法是把它前面的正数都取了, (不拿白不拿)

在选一个负数之前, 最好把它后面的负数都拿了

我们扫一遍数组, 对于每一个数, 假设一个暂时的答案包含这个数, 那么最优的解法就是

把截止这个数之前的正数都取了, 把从这个数开始到末尾的负数都取了

(因为假设有取这个数,那么这个数前面的负数肯定不会取, 否则就会把这个数删了)

这个数后面的正数也不用取, 这本文思想的关键之一,乍一看这样怎么会使最终答案最优呢?

别忘了我们在遍历数组,如果还需要取后面的正数, 在遍历到后面的时候自会取到

我们并不是要一次模拟得出最终答案,对于一些"选与不选的问题"可以考虑"假设最终答案有选这个"的思想,在遍历(暴力枚举) 的过程中得到正确的答案

ac 代码

#include<bits/stdc++.h>
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define all(x) (x).begin(),(x).end()
#define endl '\n'
#define int long longconst int N=2e5+5;
int a[N];
int pre[N];
int tot[N];
void solve(){int n;cin>>n;rep(i,1,n)cin>>a[i];rep(i,1,n){if(a[i]>=0)pre[i]=pre[i-1]+a[i];else pre[i]=pre[i-1];}tot[n]=(a[n]>=0?0:-a[n]);for(int i=n-1;i>=1;i--){if(a[i]<0)tot[i]=tot[i+1]-a[i];else tot[i]=tot[i+1];}int ans=0;rep(i,1,n){ans=max(ans,pre[i]+tot[i]);}cout<<ans<<endl;/*以下没用, 是之前试图用模拟来做的解法*/// int ans=0;// int l=1,r=n;// while(l+1!=r){//     if(a[l]>=0){ans+=a[l++];continue;}//     if(a[r]<0){ans-=a[r--];continue;}//     while(a[l]<0&&l+1!=r)l++;//     while(a[r]>=0&&l+1!=r)r--;//     if// }// rep(i,1,n){//     if(a[i]>=0){//         ans+=a[i];//     }else{//         int p=i;//         while(p<=n&&a[p]<0)p++;//         p-=1;//         if(p==n){//             ans+=(tot[n]-tot[i-1]);//             break;//         }//         if((tot[p]-tot[i-1])<a[p+1]){//             ans+=a[p+1];//             i=p;//         }else{//         }//     }// }// cout<<ans<<endl;
}signed main(){ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);int _;cin>>_;while(_--)solve();return 0;
}

题目来自 Codeforces Round 1005 (Div. 2) C. Remove the Ends

后记: 杰哥说如果你想不到这种做法,说明你还得练