免责声明:本文提供的信息仅用于教育目的,不应被视为专业投资建议。在做出投资决策时进行自己的研究并谨慎行事非常重要。投资涉及风险,您做出的任何投资决定完全由您自己负责。
在本文中,您将了解什么是均值回归交易算法?如何使用 Python 来实现这一点?
将解释 3 种不同的实现:
- 基本的
- Z 分数
- 统计套利
什么是均值回归交易算法?
均值回归是一种算法,表明价格倾向于恢复到其长期平均值。当股价偏离其历史平均值时,就意味着该资产被超买或超卖。然后,可能会触发交易信号来卖空或买入该工具,并期望其价格将恢复到平均值。
在下文中,您将看到均值回归算法的不同实现。
加载数据集:
在第一个和第二个实现中,我们将使用 Netflix 历史价格:
def download_stock_data ( ticker,timestamp_start,timestamp_end ): url= f"https://query1.finance.yahoo.com/v7/finance/download/ {ticker} ?period1= {timestamp_start} &period2= {timestamp_end} &interval\
=1d&events =history&includeAdjustedClose=true"df = pd.read_csv(url) return df datetime_start=dt.datetime( 2022 , 1 , 1 , 7 , 35 , 51 )
datetime_end=dt.datetime.today() # 转换为时间戳:timestamp_start= int(datetime_start.timestamp())
timestamp_end= int (datetime_end.timestamp()) ticker= 'NFLX'df = download_stock_data(ticker,timestamp_start,timestamp_end)
df = df.set_index( '日期' )
df.head()
实施 N°1:基本
步骤如下:
- Netflix 20天移动平均价格计算
- 计算价格与该移动平均线之间的差异
- 如果差异为正,则触发卖单。当差额为负数时,就会触发买单。
一方面,如果差值为正,则意味着价格高于 20 日移动平均线。这意味着该资产已超买,它将恢复(减少)至该平均值。因此,卖出订单被触发。
另一方面,如果差值为负,意味着资产超卖,它往往会增加并达到其平均值,从而触发买入订单。
Python代码
我在这张图中绘制了价格与其 20 天移动平均线的关系:
window = 20df[ "ma_20" ] = df[ "Adj Close" ].rolling(window=window).mean()
df[ "diff" ] = df[ "Adj Close" ] - df[ "ma_20" ]
df [ 'signal' ] = np.where(df[ "diff" ] > 0 , - 1 , 1 ) Figs=( 8 , 4 ) df[[ 'Adj Close' , "ma_20" ]].plot(figsize=figs )
plt.title( "均值回归" )
plt.show() df[ 'diff' ].情节(无花果大小=无花果)
#我将信号乘以20能够在图表中清楚地显示出来
( 20 *df[ 'signal' ]).plot(figsize=figs, linestyle= '--' )
plt.title( "Diff vs Signal" )
plt.legend()
plt.show() (df[ "Adj Close" ]/df[ "ma_20" ] ).plot(figsize=figs)
plt.title( "Ratio=Close/ma_20" )
plt.show()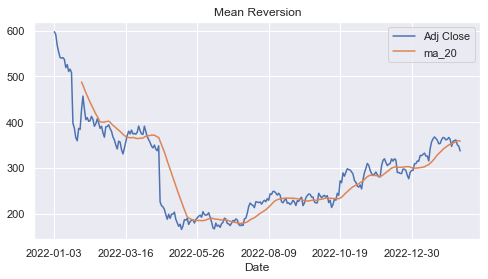
我在这张图中绘制了差异(价格 - 20 天移动平均线)和信号。它显示何时触发买入和卖出订单:

在这张图中,我绘制了价格与其移动平均线之间的比率。目标是了解该比率如何振荡。如果在 1 左右,则意味着价格正在恢复到移动平均线。我们可以清楚地看到,2022年4月有一个很大的跳跃。

局限性:
正如您所看到的,在 2022 年 4 月期间,股票价格出现了大幅下跌,并持续了几个月。如果我们遵循基本实施,就会触发买入订单。此时买入将导致接下来几天和几个月的巨大损失。这就是为什么需要将此实现与其他指标结合起来,或者选择不同的计算方法。
回测策略:
正如之前所注意到的,2022 年 4 月的价格大幅下跌严重影响了该策略的表现:
# 回测策略
# 计算每日收益
df[ 'returns' ] = df[ 'Adj Close' ].pct_change() # 计算策略收益
df[ 'strategy_returns' ] = df[ 'signal' ] .shift( 1 ) * df[ 'returns' ] # 计算累积收益
df=df.dropna()
df[ 'cumulative_returns' ] = ( 1 + df[ 'strategy_returns' ]).cumprod() Figs = ( 8 , 4 )
# 绘制累积回报
df[ 'cumulative_returns' ].情节(无花果大小=无花果)
plt.title( "累计回报" )
plt.show()
实施 N°2:z 分数
该实现可用于量化交易算法:
- 计算20天移动平均价
- 计算 20 天的标准差
- z 分数的计算方法:
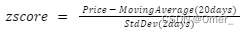
如果价格穿过上限(20 天移动平均线 + n_std 标准差),则会触发卖单。这意味着该工具已超买。
如果价格低于下限(20 天移动平均线 - n_std 标准差),则会触发买入订单。
Python代码
window= 20 # 计算50日均线
df[ 'ma_20' ] = df[ 'Adj Close' ].rolling(window=window).mean() # 计算10日均线的标准差
df[ 'std_20' ] = df[ '调整关闭' ].rolling(window=window).std() # 计算 z 分数(偏离平均值的标准差数)df[ 'zscore' ] = (df[ 'Adj Close' ] - df[ 'ma_20' ]) / df[ 'std_20' ] #如果 z 分数小于 n_std (=1),则买入订单
# 如果 z 分数大于 n_std (=1),则卖出订单
# 如果在 -1 到 1 之间,则持有
n_std= 1.25df[ '信号' ] = np.where(df[ 'zscore' ] < -n_std, 1 , np.where(df[ 'zscore' ] > n_std, - 1 , 0 )) Figs=( 8 , 4 )
df[ 'signal' ].plot(figsize=figs, linestyle= "--" )
df[ 'zscore' ].plot(figsize=figs)
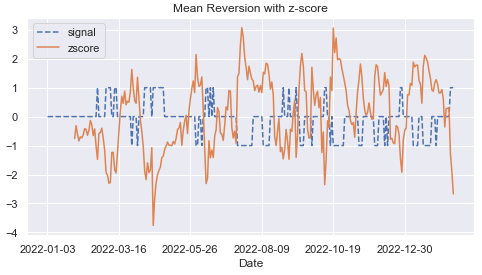
plt.title( "带有 z 分数的均值回归" )
plt.图例()
plt.show()在此图中,我们有 z 分数,以及买入或卖出订单的交易信号:
upper_band=df[ 'ma_20' ]+n_std*df[ 'std_20' ]
lower_band=df[ 'ma_20' ]-n_std*df[ 'std_20' ] Figs=( 10 , 6 )
df[ 'Adj Close' ].plot (figsize=figs)
df[ 'ma_20' ].plot(figsize=figs,linestyle= '-.' , color= "w" )
upper_band.plot(linestyle= '--' ,label= 'upper_band' )
lower_band.情节(线型= ':',标签= 'lower_band')
plt.fill_ Between(df.index,lower_band,upper_band,阿尔法 = 0.3 )
plt. 标题(“上限和下限” )
plt.legend()
plt.show()通过此图,我们可以清楚地看到价格何时超出范围。通过突破上限,股票变得超买,这是进入空头头寸的信号。
当价格下跌并突破下轨时,股票就会超卖,这可以被视为买入信号订单。

回测策略
# 计算每日收益
df[ 'returns' ] = df[ 'Adj Close' ].pct_change() # 计算策略收益
df[ 'strategy_returns' ] = df[ 'signal' ] .shift( 1 ) * df[ ' returns' ] # 计算累计收益
df=df.dropna()
df[ 'cumulative_returns' ] = ( 1 + df[ 'strategy_returns' ]).cumprod() # 绘制累计收益
df[ 'cumulative_returns' ].plot( Figsize=figs)
plt.title ( "累计回报" )
plt.show()当 n_std=1.25 时,该策略表现出良好的性能:
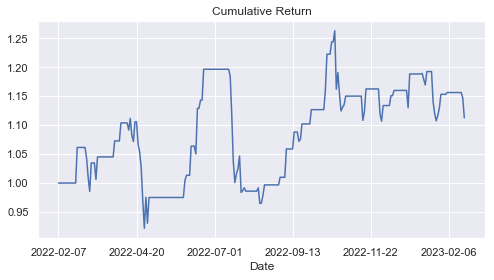
尝试修改这个数字,了解它对整体性能的影响
比较
通过添加股票在触发买入或卖出订单之前必须偏离其移动平均线多少个标准差的限制,与第一段的第一次实施相比,该策略的表现变得更具吸引力。
其他
通过调整计算以适应日内价格,该实现还可用于高频交易。
- 日内价格可以采样到几秒,甚至几毫秒。
- 以秒为单位计算的滚动平均值和标准差
- 如果突破上限或下限,则会触发买入或卖出订单。
实施 N°3:统计套利
在此实施中,我们将研究两只股票之间价差的均值回归:
- 计算两只股票之间的价差
- 计算价差的 20 天移动平均线
- 计算价差 20 天的移动标准差
- z 分数的计算方法:
![]()
Python代码
加载 2 只股票的数据集:Apple 和 Google:
import pandas as pd
import datetime as dtdef download_stock_data(ticker,timestamp_start,timestamp_end):url=f"https://query1.finance.yahoo.com/v7/finance/download/{ticker}?period1={timestamp_start}&period2={timestamp_end}&interval\
=1d&events=history&includeAdjustedClose=true"df = pd.read_csv(url)return df# Determine Start and End dates
datetime_start=dt.datetime(2022, 2, 8, 7, 35, 51)
datetime_end=dt.datetime.today()# Convert to timestamp:
timestamp_start=int(datetime_start.timestamp())
timestamp_end=int(datetime_end.timestamp()) tickers=['AAPL','GOOG']df_global=pd.DataFrame()
for ticker in tickers:df_temp = download_stock_data(ticker,timestamp_start,timestamp_end)[['Date','Adj Close']]df_temp = df_temp.set_index('Date')df_temp.columns=[ticker]df_global=pd.concat((df_global, df_temp),axis=1)
df_global.head()
指标计算
# Calculate the spread between two stocks:
ticker_long = 'AAPL'
ticker_short = 'GOOG'
spread = df_global[ticker_long] - df_global[ticker_short]window = 20
n_std = 1.5# Calculate the rolling mean and standard deviation of the spread
rolling_mean = spread.rolling(window=30).mean()
rolling_std = spread.rolling(window=30).std()# Calculate the z-score (number of standard deviations away from the rolling mean)
zscore = (spread - rolling_mean) / rolling_stdupper_band = rolling_mean + n_std * rolling_std
lower_band = rolling_mean - n_std * rolling_std现在我们绘制不同的指标来查看价差与下限和上限的表现如何:
figs=(8,4)
plt.figure(figsize = figs)
spread.plot(label='Spread = '+ticker_long+' - '+ ticker_short,linestyle='--')
df_global[ticker_long].plot(label=ticker_long+'_price')
df_global[ticker_short].plot(label=ticker_short+'_price')
plt.title("Spread and Prices of {0} and {1}".format(ticker_long,ticker_short))
plt.legend()
plt.show()plt.figure(figsize = figs)
upper_band.plot(label='Upper_band')
lower_band .plot(label='Lower_band')
spread.plot(label = 'Spread = '+ticker_long+' - '+ ticker_short,linestyle='--', color='r')
rolling_mean.plot(label = 'ma_30days_spread', linestyle = '-.')
plt.fill_between(df_global.index,lower_band, upper_band, alpha=0.2)
plt.legend()
plt.show()价差已突破或低于上限和下限。因此给出了买入或做空价差的交易信号:

回测策略
# Enter a long position if the z-score is less than -n_std
# Enter a short position if the z-score is greater than n_std
signal = np.where(zscore < -n_std, 1, np.where(zscore > n_std, -1, 0))
signal = pd.Series(signal, index=df_global.index)# Calculate the daily returns
returns = df_global[ticker_long].pct_change() - df_global[ticker_short].pct_change()# Calculate the strategy returns : # Shift the signal by one day to compute the returns
strategy_returns = signal.shift(1) * returns# Calculate the cumulative returns
cumulative_returns = (1 + strategy_returns).cumprod()# # Plot the cumulative returns
cumulative_returns.plot(figsize = figs)
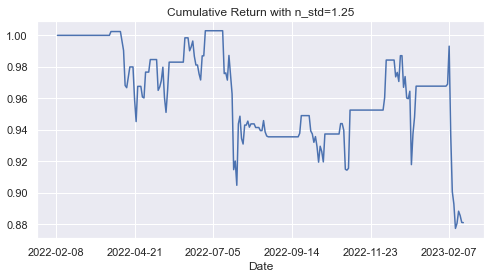
plt.title("Cumulative Return with n_std={0}".format(n_std))
plt.show()该策略产生的累积回报在整个期间显示出正值。
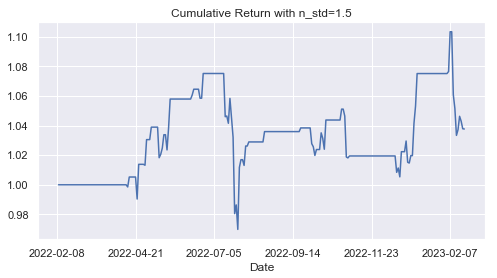
通过修改模型中的标准差数量 (n_std),您将看到对策略性能的影响。当n_std=1.25时,性能较差。