\(A. Kamilka and the Sheep\)
\(很简单的题 直接通过观察可以发现和gcd的辗转相减法有关 答案就是最大-最小\)
点击查看代码
void solve(){int n;cin>>n;vector<int>a(n);for (int i=0;i<n;i++) {cin>>a[i];}sort(all(a));cout<<a[n-1]-a[0]<<'\n';
}
点击查看代码
void solve(){int n;cin>>n;string a,b;cin>>a>>b;int even=n/2,odd=n/2+n%2;int cnt_odd=0,cnt_even=0;for (int i=0;i<n;i++) {if (i%2==0) {cnt_odd+=(a[i]=='0');}else cnt_even+=(a[i]=='0');}for (int i=0;i<n;i++) {if (i%2==0) {cnt_even+=(b[i]=='0');}else cnt_odd+=(b[i]=='0');}if (cnt_even>=even&&cnt_odd>=odd) {cout<<"Yes\n";}else cout<<"No\n";
}
\(C. Asuna and the Mosquitoes\)
\(非常简单的一道题 但是赛时脑子抽了写了半天\)
\(易得如果偶数不存在或者奇数不存在那么这题是无法流通的也就是直接取最大值即可\)
\(那么如果奇偶同时存在 我们先可以想到将所有的奇数可以在只保留1的情况下转移到一个偶数上而不改变其奇偶 所有的偶数又可以不改变奇偶的转移到一个奇数上\)
\(那么答案就是所有数的和-奇数的个数+1(因为最后放到一个奇数上必定是最大的)\)
点击查看代码
void solve(){int n;cin>>n;int cnt0=0,cnt1=0,mx=0,sum=0;vector<int>a(n);for (int i=0;i<n;i++){cin>>a[i],sum+=a[i],mx=max(mx,a[i]);if (a[i]&1)cnt1++;else cnt0++;}if (!cnt1||!cnt0){cout<<mx<<'\n';return;}sum-=cnt1-1;if (sum%2==0)sum++;cout<<sum<<'\n';
}
\(D. Mishkin Energizer\)
\(非常简单的一道构造\)
\(可以发现如果存在两个不同的字母 那么必定可以通过将每个未达到n的个数的字母插入\)
\(最终对其实现满插 即为每个字母的个数都为n\)
\(因为数据范围很小 直接模拟即可\)
\(唯一有点困难的就是实现部分\)
\(如果使用string的substr可能会导致超时\)
\(如果我们巧妙地使用链表即可解决该问题\)
点击查看代码
const int N=1e5+10;
int nxt[N];
void solve() {int n;cin>>n;int top=n-1;string s;cin>>s;set<char>S;for (auto c:s)S.insert(c);if (s.size()==1||S.size()==1) {cout<<-1<<'\n';return;}int cnt0=0,cnt1=0,cnt2=0;for (int i=0;i<n;i++) {if (s[i]=='L')cnt0++;else if (s[i]=='I')cnt1++;else if (s[i]=='T')cnt2++;}// cout<<2*n<<'\n';nxt[n]=-1;vector<int>ans;for (int i=0;i<s.size()-1;i++) {nxt[i]=i+1;}int head=0;auto pd=[&](char a,char b) {if (a=='T'&&b=='I')return 'L';swap(a,b);if (a=='T'&&b=='I')return 'L';if (a=='I'&&b=='L')return 'T';swap(a,b);if (a=='I'&&b=='L')return 'T';if (a=='T'&&b=='L')return 'I';swap(a,b);if (a=='T'&&b=='L')return 'I';};auto cal=[&](char c) {if (c=='L')return cnt0;if (c=='I')return cnt1;if (c=='T')return cnt2;};auto insert=[&](int id,int now) {int Nxt=nxt[id];nxt[id]=now;nxt[now]=Nxt;};for (int i=0;i<2*n;i++) {int ok=0;int cnt=1;for (int id=head;id!=-1;id=nxt[id]) {if (s[nxt[id]]!=s[id]&&cal(pd(s[nxt[id]],s[id]))<n) {ok=1;s+=(pd(s[nxt[id]],s[id]));if (s.back()=='L')cnt0++;if (s.back()=='I')cnt1++;if (s.back()=='T')cnt2++;top++;insert(id,top);ans.pb(cnt);break;}cnt++;}if (ok==0) {cout<<-1<<'\n';return;}}cout<<2*n<<'\n';for (auto &son:ans) {cout<<son<<'\n';}
}
问题描述
给定一个 $ n \times m $ 的棋盘,所有单元格初始被涂成绿色。其中有 $ k $ 个单元格已经被预先涂成黑色(1)或白色(0)。现在需要将剩余的绿色单元格涂成黑色或白色,使得整个棋盘中相邻颜色不同的单元格对数为偶数。求满足条件的涂色方案数,并对 $ 10^9+7 $ 取模。
解题思路
1. 问题转换
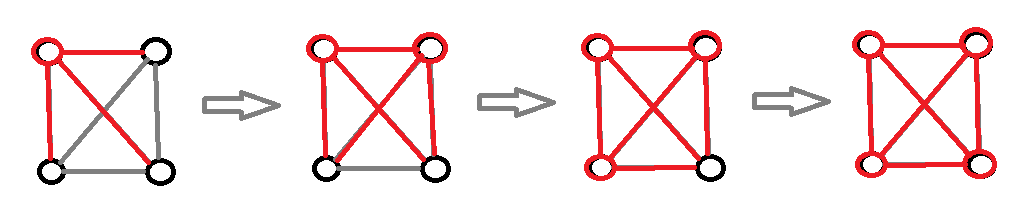
棋盘上任意两个相邻单元格,若颜色不同,则记作 1。通过分析可以发现:
- 棋盘内部单元格(非边界)的度数为偶数(如内部为 4,角落为 2),这些单元格对最终奇偶性没有影响。
- 唯一起作用的是边界但不是角落的单元格(这些单元格的度数为奇数,通常是 3)。只有这些单元格会影响最后不同色对的奇偶性。
因此,我们将问题简化为:要求所有边界非角落单元格的颜色的 XOR 和为 0(即它们的 0/1 和模 2 为 0)。
2. 统计变量
-
边界非角落单元格总数
边界非角落单元格的数量为 $ T = 2(m-2) + 2(n-2) = 2(m+n-4) $。 -
预涂色单元格统计
在 $ k $ 个预涂色单元格中,统计位于边界非角落位置的数量 $ F_{\text{fixed}} $,以及它们的颜色 XOR 和 $ P $。 -
自由涂色单元格统计
- 边界非角落单元格中未被预涂色的数量为 $ F_{\text{free}} = T - F_{\text{fixed}} $。
- 总共可以自由涂色的单元格数量为 $ \text{free_total} = n \times m - k $。
3. 方案计数
-
对于非边界非角落的自由单元格
这些单元格不影响奇偶性,每个都有 2 种涂法,总共贡献 $ 2^{\text{free_total} - F_{\text{free}}} $ 种方法。 -
对于边界非角落的自由单元格
如果有至少一个自由单元格(即 $ F_{\text{free}} > 0 $),那么在所有 $ 2^{F_{\text{free}}} $ 种涂法中,恰好一半可以使得整体边界 XOR 和为 0,也就是 $ 2^{F_{\text{free}}-1} $ 种方法。
如果 $ F_{\text{free}} = 0 $(即所有边界非角落单元格都已经预涂),那么只有当预涂的这些单元格的 XOR 和 $ P = 0 $ 时,整体条件才能满足;否则答案为 0。
可能有人会对为什么是颜色のXOR有疑问 那么首先想到如果所有位置的数都设置为0 那么总的可能一定是0 那么该种可能能够实现
继续思考又因为中间和角落无论怎么修改都是偶数 无法对结果的奇偶造成影响所以无需考虑
又因为位于边界非角落位置的数每次更改颜色 必定会引起奇偶的变化 所以他们的结果就必定为颜色的XOR和为0
4. 合并方案数
-
当 $ F_{\text{free}} > 0 $ 时,总方法数为
\[2^{(\text{free\_total} - F_{\text{free}})} \times 2^{F_{\text{free}}-1} = 2^{\text{free\_total} - 1}. \] -
当 $ F_{\text{free}} = 0 $ 时:
- 若 $ P = 0 $ ,总方法数为 $ 2^{\text{free_total}} $(因为所有自由单元格都在非边界位置,可以任意涂色);
- 否则答案为 0。
5. 快速幂算法
由于 $ \text{free_total} $ 的指数可能非常大,需要用快速幂算法对 $ 2^x $ 取模 $ 10^9+7 $。
实现代码
以下是基于上述思路的实现代码:
#include <bits/stdc++.h>
using namespace std;const int mod = 1e9 + 7;// 快速幂函数
long long qpow(long long a, long long b) {long long res = 1;while (b) {if (b & 1) res = res * a % mod;a = a * a % mod;b >>= 1;}return res;
}void solve() {long long n, m, k;cin >> n >> m >> k;// 统计预涂色单元格的信息long long cnt_fixed = 0; // 预涂色的边界非角落单元格数量long long xor_sum = 0; // 预涂色的边界非角落单元格的颜色 XOR 和for (int i = 0; i < k; i++) {long long x, y, c;cin >> x >> y >> c;// 判断是否为边界非角落单元格if ((x == 1 || x == n) ^ (y == 1 || y == m)) {cnt_fixed++;xor_sum ^= c;}}// 计算边界非角落单元格总数long long total_boundary = 2 * (m - 2) + 2 * (n - 2);// 计算自由涂色的边界非角落单元格数量long long free_boundary = total_boundary - cnt_fixed;// 总自由涂色单元格数量long long free_total = n * m - k;// 根据情况计算答案if (free_boundary > 0) {// 至少有一个自由边界单元格cout << qpow(2, free_total - 1) << '\n';} else {// 所有边界非角落单元格都已预涂色if (xor_sum == 0) {cout << qpow(2, free_total) << '\n';} else {cout << 0 << '\n';}}
}int main() {ios::sync_with_stdio(false);cin.tie(nullptr);int t;cin >> t;while (t--) solve();
}