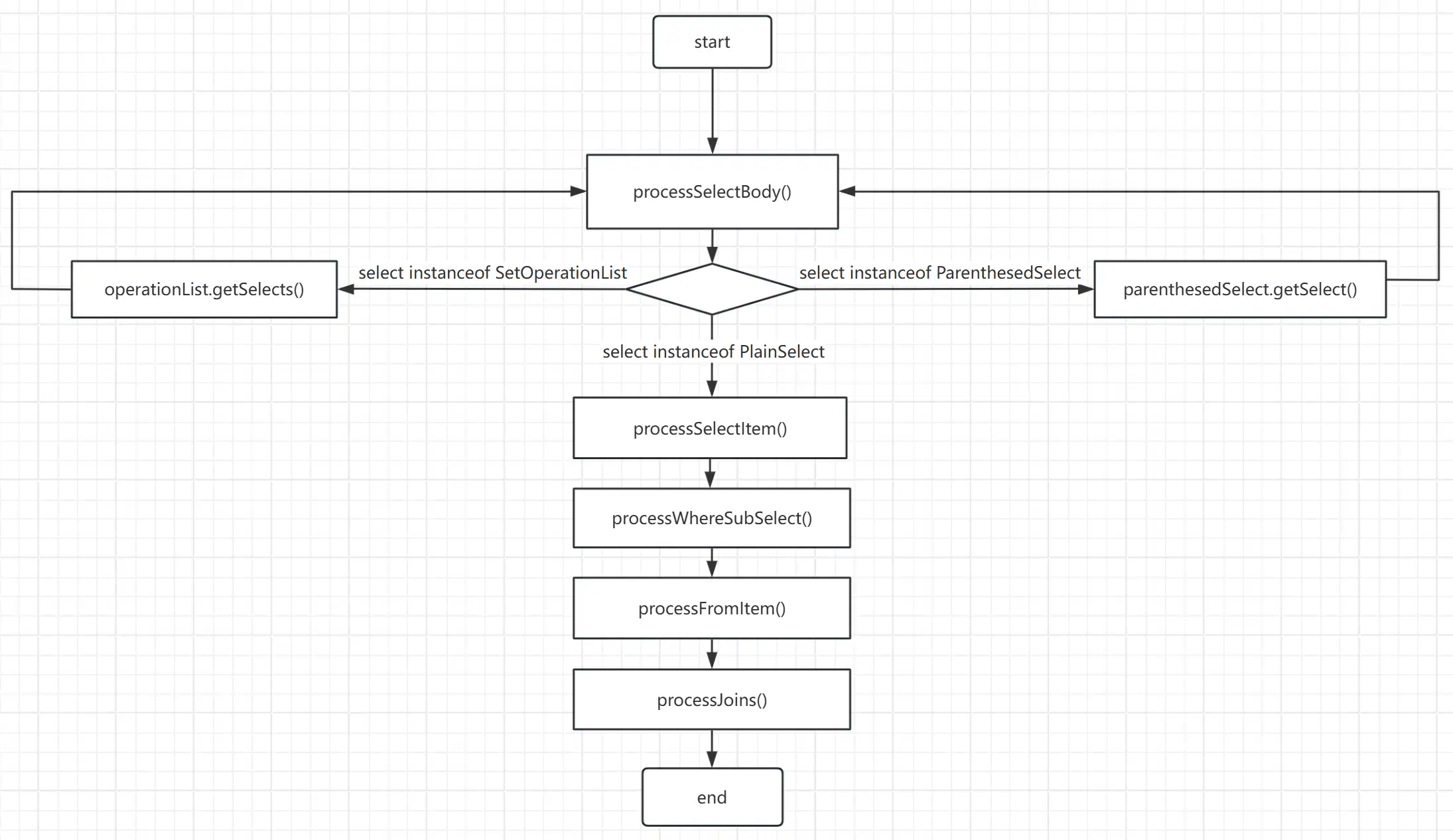
Description
JOI 大学有 \(N\) 只海狸,他们都参与竞技编程。每只海狸有三项能力值:思考值,行动值和运气值。如果一个能力值很大,意味着他这项能力比较强大。对于第 \(i~(i\in[1,N])\) 只海狸,他的思考值为 \(X_i\),行动值为 \(Y_i\),运气值为 \(Z_i\)。
今年 JOI 大学的海狸们将参与一场团体竞技编程,一支队伍由三名队员组成。Bitaro 是 JOI 大学的教练,由于团队合作很重要,Bitaro 决定从 \(N\) 只海狸中选出三只海狸组成队伍,这三只海狸要满足以下条件:
条件:每个成员都有自己的优势,这意味着每个成员都有一项能力值严格大于其他两人的对应能力值。
在所有符合条件的组队中,Bitaro 想要选一个总能力最强的队伍,一个队伍的总能力定义为:三人最大思考值,三人最大行动值和三人最大运气值之和。
请你求出,是否存在一个符合条件的组队,如果是,计算队伍总能力可能的最大值。
\(3\leq N\leq 150000\),\(1\leq X_i,Y_i,Z_i\leq 10^8\)。
Solution
首先先把 \(x,y,z\) 三维分别最大的拿出来,假设 \(x\) 最大的是 \(k\)。
那么如果 \(y_k\) 或者 \(z_k\) 仍然是最大的,\(k\) 怎么选都会不合法,就把 \(k\) 删掉。对 \(y\) 和 \(z\) 最大的做同样的事情。
这么删到最后一定满足 \(x,y,z\) 最大的位置互不相同,这三个显然就是答案。
如果只剩下不超过 \(2\) 个则无解。
时间复杂度:\(O(n\log n)\)。
Code
#include <bits/stdc++.h>// #define int int64_tconst int kMaxN = 1.5e5 + 5;int n;
int a[kMaxN], b[kMaxN], c[kMaxN];
std::set<std::pair<int, int>> sa, sb, sc;void del(int x) {sa.erase({a[x], x}), sb.erase({b[x], x}), sc.erase({c[x], x});
}void dickdreamer() {std::cin >> n;for (int i = 1; i <= n; ++i) {std::cin >> a[i] >> b[i] >> c[i];sa.emplace(a[i], i);sb.emplace(b[i], i);sc.emplace(c[i], i);}for (; sa.size() >= 3;) {int x = sa.rbegin()->second, y = sb.rbegin()->second, z = sc.rbegin()->second;bool fl = 1;if (b[x] == b[y] || c[x] == c[z]) del(x), fl = 0;if (a[y] == a[x] || c[y] == c[z]) del(y), fl = 0;if (a[z] == a[x] || b[z] == b[y]) del(z), fl = 0;if (fl) return void(std::cout << a[x] + b[y] + c[z] << '\n');}std::cout << "-1\n";
}int32_t main() {
#ifdef ORZXKRfreopen("in.txt", "r", stdin);freopen("out.txt", "w", stdout);
#endifstd::ios::sync_with_stdio(0), std::cin.tie(0), std::cout.tie(0);int T = 1;// std::cin >> T;while (T--) dickdreamer();// std::cerr << 1.0 * clock() / CLOCKS_PER_SEC << "s\n";return 0;
}