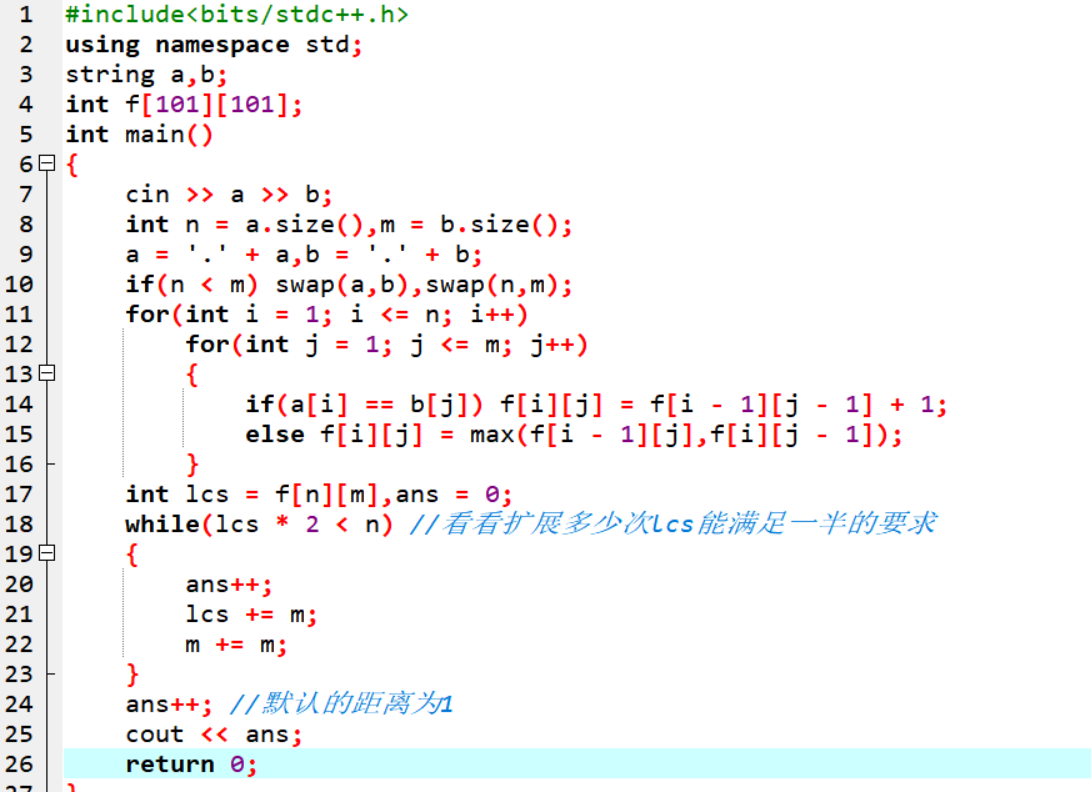
题面
首先我们发现LDRU是好维护的,重点是IC操作。我们考虑发掘一下性质将所有I和C操作移到最前面。显然UD对于I是没有影响的,可以直接交换位置即UI等价于IU,DI等价于ID,LR对C同理。
所以接下来我们只需要考虑LR对于后面的I和UD对于后面的C的影响。这里用RI举例,我们考虑一下RI的情形本质是怎么样的。我们分析一下,假设原来排列中存在 \(a_i=d\) ,经过I操作后可以得到 \(a_d=i\),而先进行R得到 \(a_{i+1}=d\),再做I操作变成 \(a_d=i+1\) 于是我们得到了一个新操作,我们令“+”表示将所有数加一。那么RI等价于I+,同理,LI等价于I-,UC等价于C-,DC等价于C+。
但是现在又有了,+和-操作与IC依然不符合交换律,所以我们继续分析,还是用I举例。考虑操作+I的本质。假设原来排列中存在 \(a_i=d\) ,经过I操作后可以得到 \(a_d=i\),而先进行+得到 \(a_i=d+1\),再做I操作变成 \(a_{d+1}=i\),所以+I操作等价于IR,同理,-I等价于IL,-C等价于CU,+C等价于CD。
现在我们就成功将操作序列转化为了一堆I/C,后面一堆+/-以及LRDU,后面的几种操作显然是满足交换率的很好做,前面的IC序列经过观察发现ICI和CIC两种操作是等价的,证明如下:将每个点看作三元组 \((i,j,a_{i,j})\),操作I后变成 \((i,a_{i,j},j)\),操作C后变成 \((a_{i,j},j,i)\),所以一个点经过上面两种变化后都会变成 \((j,i,a_{i,j})\)。而相邻的两个I或者两个C都可以抵消,所以前面的IC序列最终会等价与一个长度不超过3的序列,这道题就做完了。
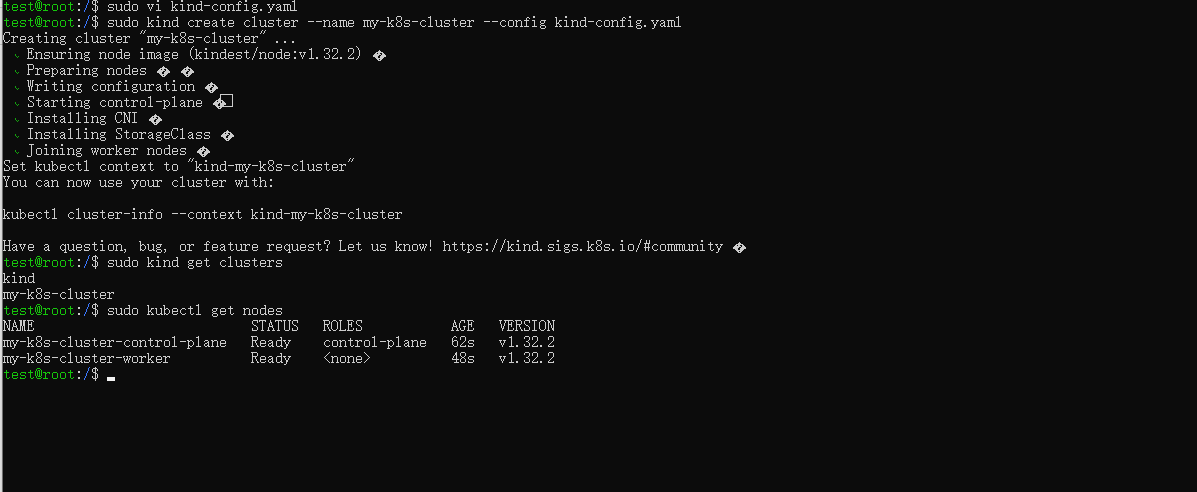


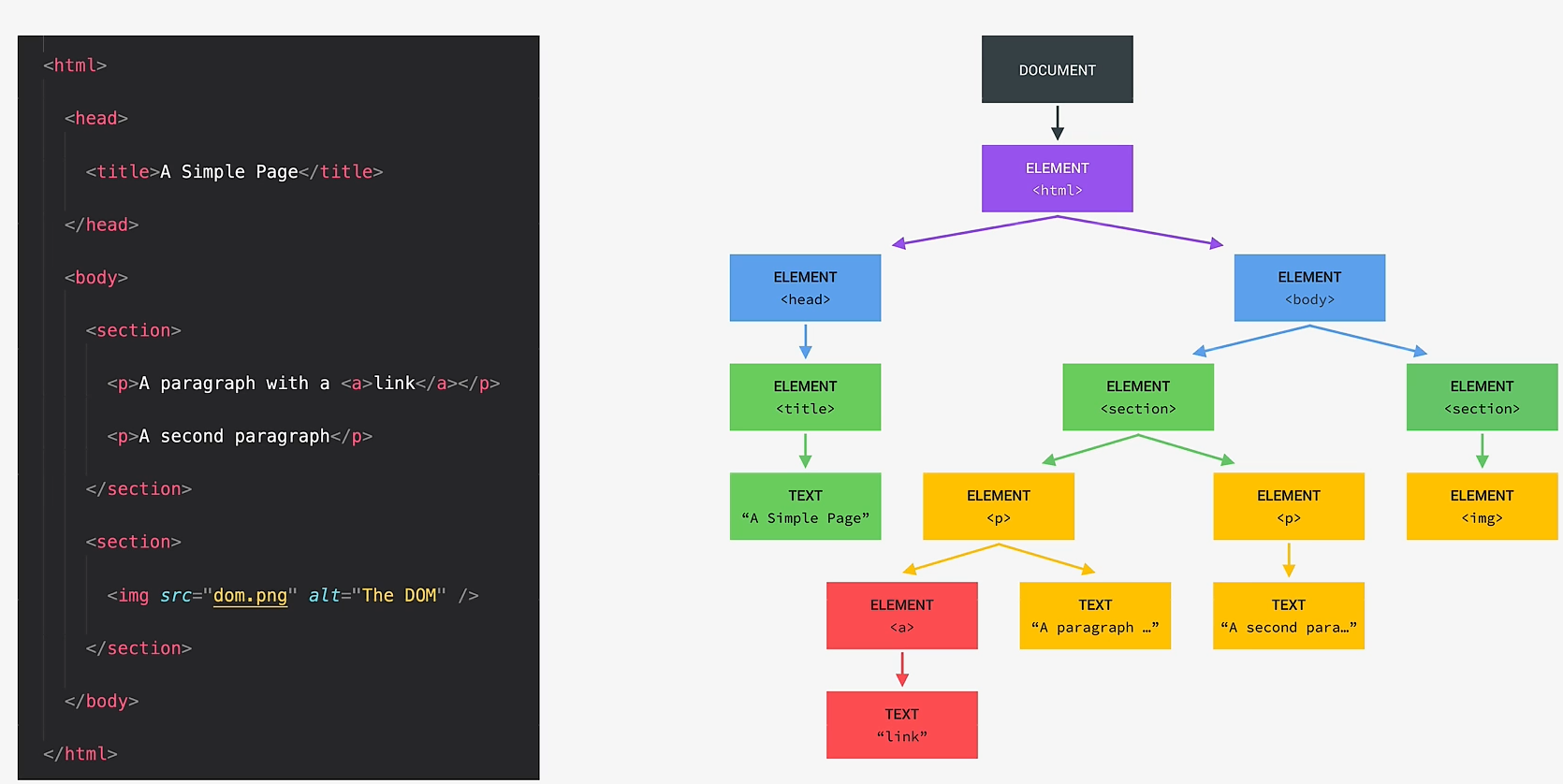

![[T.4] 团队项目:团队代码管理准备](https://img2024.cnblogs.com/blog/3611524/202504/3611524-20250401154705081-1539101818.png)