有时间窗车辆路径问题(Vehicle Routing Problems with Time Windows,VRPTW)是一类著名的组合优化问题,涉及在有限时间窗口约束下,有效地安排多个车辆的路径,以满足客户需求。
在VRPTW中,假设有一个中央仓库和一组客户节点,每个节点有特定的需求量、服务时间窗口和时间窗宽度。问题的目标是在满足以下约束条件前提下,找到一组最佳路径:
- 每个节点只能在其时间窗口内进行服务。
- 车辆在仓库出发,并返回仓库,且不超过车辆的最大行驶距离和容量限制。
- 所有客户需求量得到满足。
VRPTW是一个NP-hard问题,难以在多项式时间内获得精确解。因此,通常使用启发式和元启发式算法来近似求解。
下面是一些常用的求解VRPTW的方法:
-
基于启发式算法的方法:这类方法使用启发规则来指导路径的构建。例如,最近邻规则、最远插入规则、最优插入规则等。它们逐步构建路径,每次选择一个节点进行插入,直到所有节点都被插入路径中。
-
遗传算法和进化算法:这些算法利用基因编码和进化操作(如交叉、变异)进行全局搜索。通过利用优秀解的性质,逐代优化路径的质量。
-
禁忌搜索算法:该算法通过跳出局部最优解的搜索过程,基于禁忌表和禁忌策略来避免重复搜索相似的解。
-
模拟退火算法:这是一种随机搜索优化算法,模拟了物质在退火过程中的行为。通过渐进降低温度和接受劣质解的概率,逐渐搜索到全局最优解。
-
其他元启发式算法:如蚁群算法、粒子群算法、人工免疫算法等,这些算法模拟自然界的行为和现象,用于搜索和优化问题。
VRPTW的求解方法需要根据问题的规模和复杂性选择合适的算法。解决VRPTW不仅仅是求解最优路径,还需要进行路径规划、资源配置和优化调度,以提高效率和满足时间约束。
不同的求解方法原理不同,适用场景也会有所差异,这里做了简要的总结分析:
-
启发式算法:启发式算法是一种基于经验的方法,通过设计一些规则或策略来指导路径的构建。例如,最近邻规则会选择距离当前节点最近的下一个节点进行插入。它们的优点包括简单易实现、计算效率高,能够在短时间内找到接近最优的解。然而,启发式算法往往局限于局部搜索,可能会陷入次优解,不保证找到全局最优解。
-
遗传算法和进化算法:遗传算法通过模拟自然界的生物进化过程,利用交叉和变异等进化操作,对路径进行全局搜索。其优点在于对多个解进行并行搜索,能够避免陷入局部最优解。然而,由于遗传算法需要进行大量的解的评估和选择操作,计算复杂度较高,并且不保证获得最优解。
-
禁忌搜索算法:禁忌搜索通过记忆搜索历史和禁忌策略来避免陷入局部最优解,并探索更广阔的搜索空间。其优点是具有较强的全局搜索能力,能够在有限的搜索时间内找到较好的解。然而,禁忌搜索算法选择何时解禁,以及禁忌表的更新策略等设计都需要进行仔细调整,不同的问题可能需要不同的禁忌思路。
-
模拟退火算法:模拟退火算法通过使用随机扰动和接受劣质解的策略,模拟物体退火时温度的下降过程,有助于跳出局部最优解。它的优势在于全局搜索能力较强,能够在搜索空间中更广泛地探索。然而,模拟退火算法的效果高度依赖于退火参数的设置,对于复杂问题可能需要长时间的搜索才能找到较好的解。
-
其他元启发式算法:蚁群算法、粒子群算法、人工免疫算法等元启发式算法根据模拟自然界的行为或现象进行路径搜索和优化。它们具有较强的全局搜索能力和适应性。然而,它们的参数设置相对复杂,计算开销较高,对于问题规模较大的情况可能不适用。
需要根据具体的问题和需求选择适当的求解方法。对于简单任务和较小的问题规模,启发式算法可能已足够满足要求;而对于复杂任务和大规模问题,进化算法、禁忌搜索或元启发式算法可能更适用。此外,可以结合多种算法进行问题求解,如启发式算法与禁忌搜索的结合使用,以充分发挥各自的优点。
最近有一个小问题可能跟这块的解决思路是一致的,就想着抽点时间先来看下VRPTW相关的知识内容,基于实际的数据来做些实践性质的工作。
实例数据集如下所示:
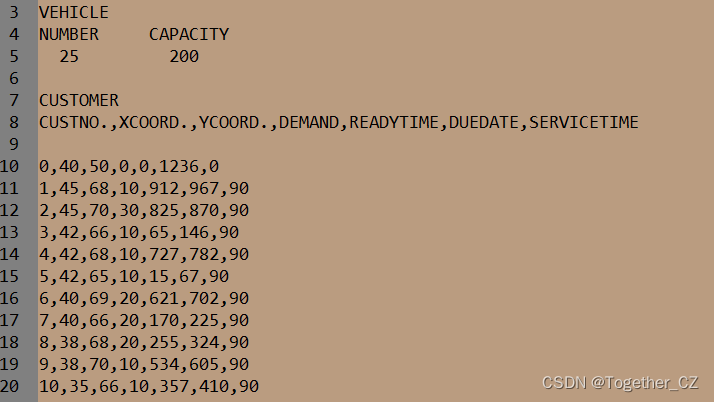
参数定义:
capacity = 200
temperature=1000
alpha=0.99
speed=1
HUGE=99999999
early_unit_cost=0.2
late_unit_cost=0.5
distance_unit_cost=1
best_sol=None对应类定义:
class Node:def __init__(self):self.name = Noneself.x = Noneself.y = Noneself.demand = Noneself.ready = Noneself.due = Noneself.service = Noneclass Sol:def __init__(self):self.path = []self.node = []self.cost=None代价计算:
def get_cost(sol):total_cost=0distance_cost=0early_cost=0late_cost=0sum_demand=0now_time=0for i in range(len(sol.path)):if i==0:continuedistance=get_distance(sol.path[i-1].x,sol.path[i-1].y,sol.path[i].x,sol.path[i].y)distance_cost+=distance*distance_unit_costnow_time+=distance/speedsum_demand+=sol.path[i].demandif sum_demand>capacity:total_cost+=HUGEif now_time<sol.path[i].ready:early_cost+=(sol.path[i].ready-now_time)*early_unit_costnow_time=sol.path[i].readyif now_time>sol.path[i].due:late_cost += (now_time-sol.path[i].due) * late_unit_costnow_time+=sol.path[i].serviceif sol.path[i].name==0:now_time=0sum_demand=0total_cost+=distance_cost+early_cost+late_costsol.cost=total_costreturn total_cost局部搜索:
def local_search(sol):global best_soltemp_sol=copy.deepcopy(sol)temp2_sol=copy.deepcopy(sol)for i in range(10):change(temp2_sol)if get_cost(temp2_sol)<get_cost(temp_sol):temp_sol=copy.deepcopy(temp2_sol)c1=get_cost(temp_sol)c2=get_cost(sol)if c1<c2:if c1<best_sol.cost:best_sol=temp_solsol=temp_solelse:if np.exp((c2-c1)/temperature)<random.random():sol = temp_solreturn sol实例执行:
sol=read_data()
init_code(sol)
print(get_cost(sol))
best_sol=copy.deepcopy(sol)
cost=[]
for i in tqdm(range(2000)):sol=local_search(sol)cost.append(sol.cost)temperature*=alpha
plt.clf()
plt.plot(cost)
plt.savefig("cost.png")
plot(best_sol)
print([best_sol.path[i].name for i in range(len(best_sol.path))])
终端输出如下所示:

对路径搜索做了记录可视化如下所示:

代价计算曲线如下所示:
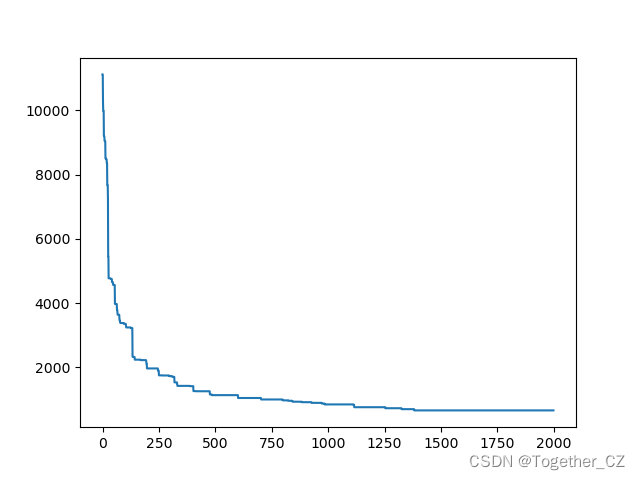
随着搜索迭代cost趋于稳定。