文章目录

实现原理
- 基础位运算
- 位图思想
- 找最右侧数
- 按位异或
算法思路
典型例题
- 基础位运算
- - 只出现一次的数字
  - 只出现一次的数字III
- 经典题型
- - 判断字符是否唯一
  - 两整数之和
  - 只出现一次的数字II
  - 消失的两个数字
鸽巢原理
总结

本篇总结位运算中常见的算法题和思路，首先总结位运算中常见的题型

实现原理

基础位运算

位运算主要包含

左移 <<
右移 >>
按位取反 ~
按位与 &
按位或 |
按位异或 ^

位图思想

1. 给定一个数n，确认它的二进制表示中第x位是0还是1

解法：(n>>x) & 1
原理：n右移x个单位，就令所求元素的二进制位移动到了第一位，再令其和1按位与，其他位都是0，只有第一位，如果n的这个位置为1，则结果为1，如果是0，则结果为0

2. 给定一个数n，将它的二进制表示的第x位改成1

解法：(1<<x) | n
原理：将1左移x个单位，就可以让二进制表示中1挪动到x的位置，再让这个左移后的1和n按位或，则就可以改变这个位置的0

3. 将一个数n的二进制表示的第x位修改成0

解法：(~(1<<x)) & n
原理：将1左移x个单位，此时除了第x位置外，其余位置都为0，再令其按位取反，此时除了第x个位置外，其余地方都为1，再让这个数和n按位与，此时其余位置不变，第x的位置就会被改变为0

找最右侧数

1. 提取一个数n二进制中最右侧的1

解法：n & -n
原理：-n的原理是按位取反再+1，将最右侧的1，左边的区域全部取反就是-n

以下图例子为例：

在这里插入图片描述

2. 去掉一个数n二进制表示中最右侧的1

解法：n & (n-1)
原理：n-1就可以把最后一个1右侧的部分全部取反，此时按位与即可

按位异或

主要应用场景是单身狗等问题

算法思路

算法思路主要就是前面的这些原理，而大部分题目就是基于上面的原理进行一些叠加，只需要把题目进行一定程度的拆分，就可以解题了

典型例题

基础位运算

位运算在前面已经学过一些，这里主要总结一些比较常见的，比较有典型的例子，较简单的不归纳

只出现一次的数字

class Solution 
{
public:int singleNumber(vector<int>& nums) {int ret=0;for(auto ch : nums){ret^=ch;}return ret;}
};

这里主要就是用到了按位异或的性质，按位异或的一个重要性质就是，如果一组数中每一个元素出现的此时都是偶数，只有一个是奇数，那么只需要把这个数组中所有的数据都按位异或起来，最终剩下的数就是那个数，这是由于按位异或自身的原理所产出的算法原理

只出现一次的数字III

class Solution 
{
public:vector<int> singleNumber(vector<int>& nums) {int ret=0;for(auto ch :nums){ret=ret^ch;}int lsb= ret==INT_MIN? ret:(ret&(-ret));int type1=0,type2=0;for(auto num:nums){if(num &lsb){type1 ^=num;}else{type2 ^=num;}}return {type1,type2};}
};

这个题本身就是基于上面题目的原理产生的，按位异或可以找到一组数中唯一出现的数，那么在这个题中却有两个数都唯一出现的，那么首先要做的就是进行分类，让这两个数归类到两个类中，以此能让其分开

那么分类的原理就是让所有数都按位异或，最终得到的就是这两个数按位异或的结果，那现在要做的就是要找到这两个数的不同点，然后把这两个数分开，具体方法就是用到了前面总结的找到不一样的1，令ret&(-ret)，这样就可以找到二进制中最右侧的1，而这个1就是区分这两组数据的唯一标准

那下来做的就是把nums中的元素都和前面ret&(-ret)的结果按位异或，由于最右侧1的不同，就会天然的把数组里面的数据分成两组，而这两个不同的数据也会被分到两组中，这样找到了唯二的数据

经典题型

判断字符是否唯一

这里解决方法很多，可以用哈希表，排序，等等，这里采用是位图的思想，同时利用鸽巢原理进行一定程度的优化

class Solution 
{
public:bool isUnique(string astr) {if(astr.size()>26){return false;}int bitmap=0;for(auto ch : astr){if((bitmap>>(ch-'a'))&1==1){return false;}else{bitmap=bitmap | (1<<(ch-'a'));}}return true;}
};

两整数之和

此题需要用到按位与和按位异或的性质，按位与的性质除了相同为0，相异为1外，还有一个性质是无进位相加，因此可以利用这个性质解题，先用按位异或进行无进位相加，再求出进位是多少，再继续循环相加即可

而进位其实就是直接用的性质是两个数的二进制位都为1，则要进1，如果有一个为0则为0，其实这就是按位与的操作，但是由于进位要进1，因此这里把运算出的结果左移一个单位其实就是最终的结果，那么依据这个原理就可以求出最终的结果，当进位为0的时候循环结束

class Solution {
public:int getSum(int a, int b) {while(b!=0){int x=a^b;int carry=(a&b)<<1;a=x;b=carry;}return a;}
};

只出现一次的数字II

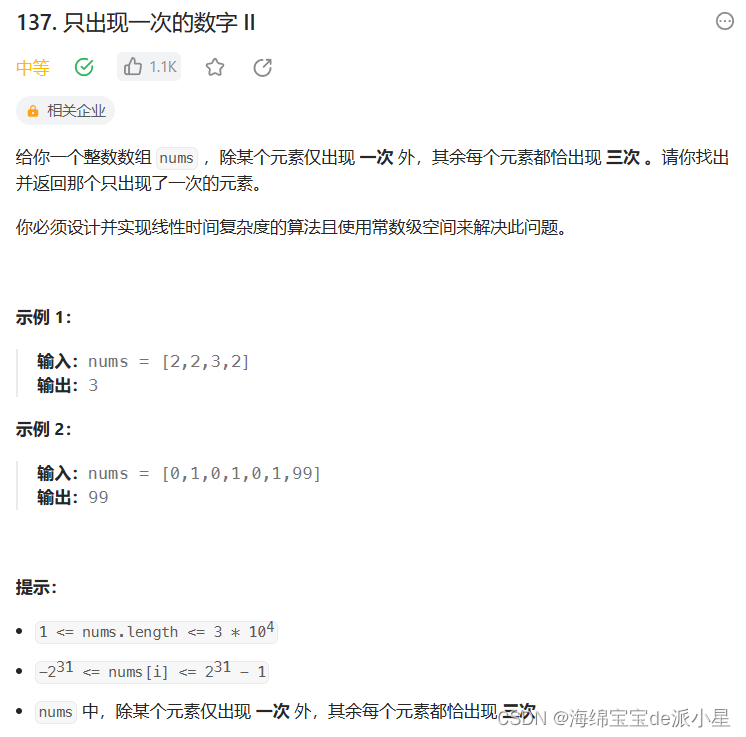
对于这个题首先可以采用哈希表的方法解决，但更好的方法是使用位运算，需要一定的观察

这里采用的是比特位计数的方法，原理就是通过观察这些数，找到每一个单独的比特位拥有的独特的规律，那对于这个题来说，规律就是对于数组nums，它当中每一个数的某一个比特位相加，最终相加的结果%3得到的就是这唯独一个数据的比特位的值，下图来解释

这里是举了具体的例子，如果把它抽象成字母来代表其中的数据，其实也是一样的，因为数字要不然是三个一组，要不然一个一组，而三个一组的数据最终都能被三整除，最后唯独不同的就是一个一组的数据

利用这个原理，就能很轻松的把原来的ret的每一个比特位都得到，得到每一个比特位最终这个数就是我们要求的数据

class Solution 
{
public:int singleNumber(vector<int>& nums) {int ret=0;for(int i=0;i<32;i++){int sum=0;for(auto ch:nums){sum+=(ch>>i) & 1;}sum%=3;ret = ret | (sum<<i);}return ret;}
};

消失的两个数字

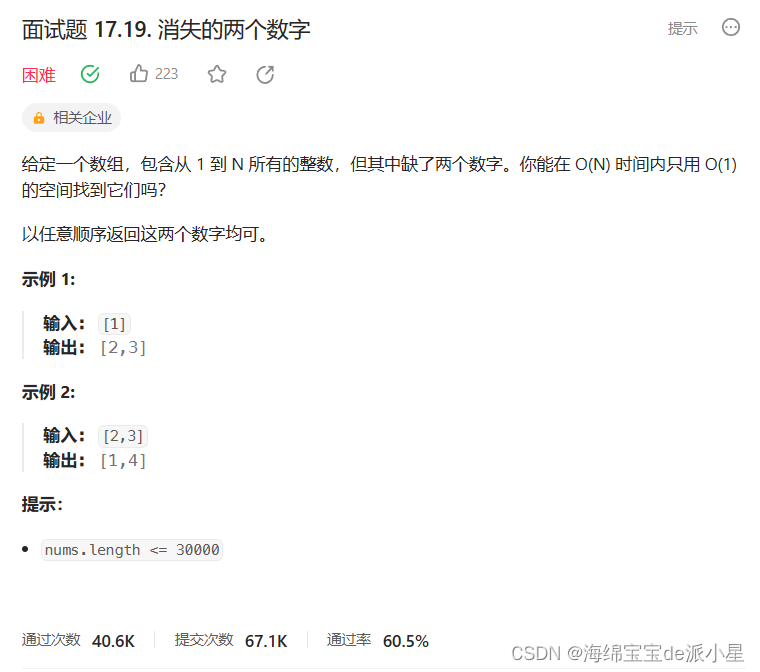
本题实现原理其实就是前面两个题的结合，分别是消失的数字和只出现一次的数字III，但这个题的解法还有很多种，其中一种是借助鸽巢原理进行排序解决，也是一种思维较为巧妙的一种解法，可以借鉴学习

下面展示的是位运算的传统解法，鸽巢原理后续进行补充

class Solution 
{
public:vector<int> missingTwo(vector<int>& nums) {int n=nums.size();// 找到两个数按位异或的结果int ret=0;for(int i=1;i<=n+2;i++){ret ^= i;}for(auto ch : nums){ret ^= ch;}// ret就是两个数按位异或的结果// 现在把这两个数分开找到即int lsb=ret&(-ret);    // 找到不同点int type1=0,type2=0;for(int i=1;i<=n+2;i++){if(i & lsb){type1 ^= i;}else{type2 ^= i;}}for(auto p : nums){if(p & lsb){type1 ^= p;}else{type2 ^= p;}}return {type1 , type2};}
};

鸽巢原理

鸽巢原理的概念就是，如果有n+1个鸽子飞进了n个鸽巢中，那么必定有鸽巢中至少飞进了2只鸽子

其实在前面的题目中，也有部分题可以使用鸽巢原理进行解决，例如在哈希表的使用中就经常可以用到鸽巢原理进行一定程度的优化，例如判断一个字符串中每个字符只出现一次，那么此时，如果字符串的长度大于26，那么说明这里必定会不是我们所要找的

类似的题目还有很多，但是对于上面的题目一个很简单的方法就是借助鸽巢原理进行排序来解决题目

依据这个原理，可以实现一个时间复杂度只有O(N)的排序，但是这个排序有一定的条件，条件就是要排序的数组必须是从1到n中所有数，并且每个数只出现一次，依据这个原理就可以解决问题

void sort(vector<int>& nums)
{  //6,1,2,5,-1,-1for (int i = 0; i < nums.size(); i++) {while (nums[i] != -1 && nums[i] != i + 1){swap(nums[i], nums[nums[i] - 1]);}}
}int main()
{vector<int> v{ 6,1,2,5,-1,-1 };sort(v);return 0;
}