周赛题目
2760. 最长奇偶子数组
2761. 和等于目标值的质数对
2762. 不间断子数组
2763. 所有子数组中不平衡数字之和
一、最长奇偶子数组
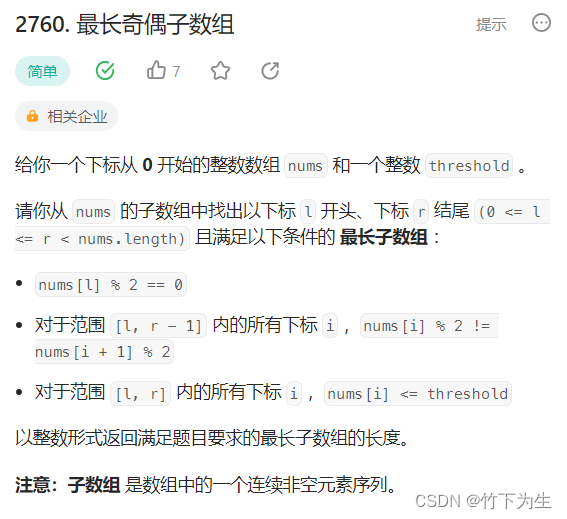
这题的数据范围允许用暴力来做,只要我们分别枚举左端点left和右端点right,然后看区间[left,right]是否符合题目条件,然后找到最大值了返回就行,这里就不多做解释了,下面讲解一种更快的算法---滑动窗口
思路:我们先找到符合条件的左端点,再不断向右扩展右端点,并不断更新最长子数组的长度,直到遇到不符合条件的数出现,我们再移动左端点,使得区间再次符合条件,然后继续移动右端点,如此循环,最后返回得到的最长子数组的长度
代码如下
int longestAlternatingSubarray(int* nums, int numsSize, int threshold){int right=0;int ans=0;while(right<numsSize){//找到符合条件的左端点if(nums[right]>threshold||nums[right]%2){right++;continue;}int left=right;right++;while(right<numsSize&&nums[right]<=threshold&&(nums[right-1]%2)!=(nums[right]%2)){ right++;}ans=fmax(ans,right-left);}return ans;
}二、和等于目标值的质数对
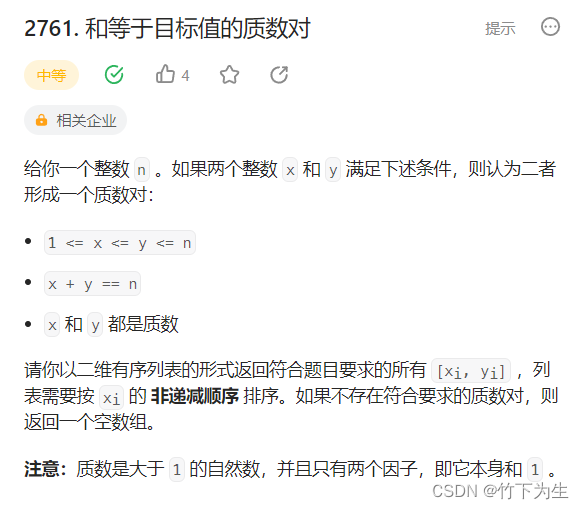
这题其实也不难,主要是质数的判断比较费时间,如果我们一个个去比较,那么时间很可能会超时,这里需要用埃氏筛或者线性筛,来提前预处理出那些素数
这里简单说明一下埃氏筛的思路:默认所有的数都是素数(即标记为true),从2开始枚举,将2放入素数集合中,再将范围内所有2的倍数标记为false,然后下一个枚举的数是如果是true,就加入素数集合,并将其在范围内的所有倍数标记为false,如果是false,就将其在范围内的所有倍数标记为false,如此循环,就得到了范围内所有的素数
代码如下
int** findPrimePairs(int n, int* returnSize, int** returnColumnSizes){bool prime[n+1];for(int i=0;i<=n;i++)prime[i]=true;for(int i=2;i<n;i++){for(int j=i;j<n/i+1;j++){//这里的写法可以防止越界prime[j*i]=false;}}int**ans=(int**)malloc(sizeof(int*)*100000);*returnSize=0;for(int i=2;i<n;i++){if(!prime[i])continue;if(n-i<i)break;if(prime[n-i]){int*tmp=(int*)malloc(sizeof(int)*2);tmp[0]=i,tmp[1]=n-i;ans[(*returnSize)++]=tmp;}}*returnColumnSizes=(int*)malloc(sizeof(int)*(*returnSize));for(int i=0;i<*returnSize;i++){(*returnColumnSizes)[i]=2;}return ans;
}进阶:由于埃氏筛会导致有些数字被重复赋值为false,浪费了时间(如12=2*6=3*4),这里补充讲一下线性筛,也就是防止重复赋值的情况,我们该怎么办?我们只要将枚举到的数字和已经得到的质数相乘,且如果该质数是所枚举数字的因子,直接跳出循环即可,这个算法的证明有兴趣的同学可以自行去百度,这里就不做详细证明了,写一下代码
int** findPrimePairs(int n, int* returnSize, int** returnColumnSizes){bool is_prime[n+1];int primes[n];int k=0;for(int i=0;i<=n;i++)is_prime[i]=true;for(int i=2;i<n;i++){if(is_prime[i])primes[k++]=i;for(int j=0;j<k&&primes[j]*i<n;j++){is_prime[primes[j]*i]=false;if(i%primes[j]==0)break;}}int**ans=(int**)malloc(sizeof(int*)*100000);*returnSize=0;for(int i=2;i<n;i++){if(!is_prime[i])continue;if(n-i<i)break;if(is_prime[n-i]){int*tmp=(int*)malloc(sizeof(int)*2);tmp[0]=i,tmp[1]=n-i;ans[(*returnSize)++]=tmp;}}*returnColumnSizes=(int*)malloc(sizeof(int)*(*returnSize));for(int i=0;i<*returnSize;i++){(*returnColumnSizes)[i]=2;}return ans;
}三、不间断子数组
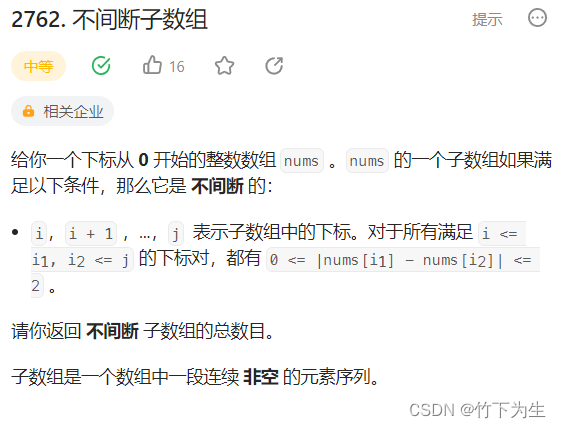
我们先用个例子来找找思路

接下来,我们只需要维护一段区间上的最大值和最小值来保证区间合法就行,那么这题很显然要用到特殊的队列(优先队列)来维护变化区间上的最大值和最小值,代码如下
long long continuousSubarrays(int* nums, int numsSize){long long ans=0;int n=numsSize;int q_Max[n],q_Min[n];int h1=0,t1=0,h2=0,t2=0;for(int left=0,right=0;right<numsSize;right++){while(h1<t1&&nums[q_Max[t1-1]]<nums[right]){t1--;}while(h2<t2&&nums[q_Min[t2-1]]>nums[right]){t2--;}q_Max[t1++]=right;q_Min[t2++]=right;while(h1<t1&&h2<t2&&nums[q_Max[h1]]-nums[q_Min[h2]]>2){if(q_Max[h1]<q_Min[h2]){h1++;}else{h2++;}//这里不用担心h1或者h2越界的问题,因为它们就算h1或者h2到达n-1,那么++的必然是另一个//而一旦h1=h2=n-1,就不符合最大值和最小值相差大于2的条件,不用进入循环left=fmin(q_Max[h1],q_Min[h2]);}ans+=right-left+1;}return ans;
}四、2763. 所有子数组中不平衡数字之和
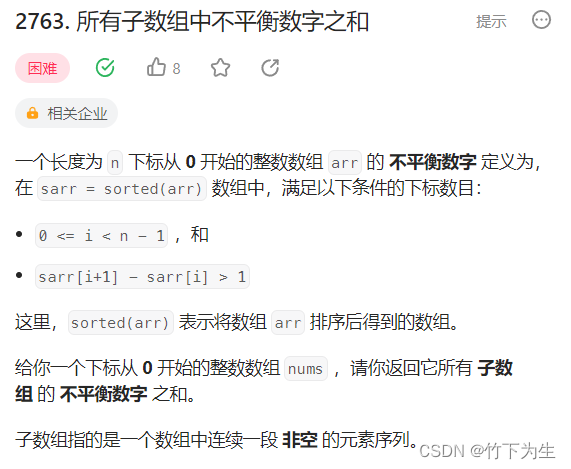

这题的数据范围允许我们使用暴力做法,即直接枚举左右端点,依次计算每个区间的不平衡数字之和,将它们相加后返回,这里的问题就在于我们如何计算区间内的不平衡数字之和,很多人就会想到题目中要求排序,那我们也排序,但是一旦排序就会改变数组中数字的顺序,所以我们就需要额外空间来存放需要排序的数字,既增加空间复杂度,又增加了时间复杂度,这里其实不用这么复杂,我们继续来举个例子帮助大家打开思路

代码如下
int sumImbalanceNumbers(int* nums, int numsSize){int n=numsSize,ans=0;for(int i=0;i<n;i++){bool visited[n+2];memset(visited,false,sizeof(visited));visited[nums[i]]=true;int cnt=0;for(int j=i+1;j<n;j++){int x=nums[j];if(!visited[x]){cnt+=1-visited[x-1]-visited[x+1];visited[x]=1;}ans+=cnt;}}return ans;
}//介绍另一种写法
int sumImbalanceNumbers(int* nums, int numsSize){int visited[numsSize+2];memset(visited,-1,sizeof(visited));int ans=0;for(int i=0;i<numsSize-1;i++){int cnt=0;visited[nums[i]]=i;for(int j=i+1;j<numsSize;j++){int x=nums[j];if(visited[x]!=i){cnt+=1-(visited[x-1]==i)-(visited[x+1]==i);visited[x]=i;}ans+=cnt;}}return ans;
}那么有没有O(n)的方法呢?
其实这题还可以用贡献法来求解,即我们来单独讨论每个元素对不平衡数字之和的贡献。
算法的思想:假设我们要计算x这个数对数组不平衡数字的贡献,那么我们向左边寻找离x最近的x-1或x,在向右边寻找离x最近的x-1(之所以不找x+1,是因为当我们计算x+1这个数的贡献时,就会向左找x,所以没必要找,而右边不找x的理由同上)这样我们就能知道x存在的子数组的个数(用乘法原理),由此来推断x对不平衡数字的贡献,但是这有一个问题:当x是所在子数组的最小值时,它的贡献就是0,我们需要减去这部分多算的贡献,而每一个元素x充当最小值的子数组的数量就是原数组的子数组的数量,也就是n(n+1)/2---注意子数组要求连续
代码如下
int sumImbalanceNumbers(int* nums, int numsSize){int n=numsSize,ans=0;int left[n];int idx[n+1];memset(idx,-1,sizeof(idx));for(int i=0;i<n;i++){int x=nums[i];left[i]=fmax(idx[x-1],idx[x]);idx[x]=i;}for(int i=0;i<n+1;i++){idx[i]=n;}for(int i=n-1;i>=0;i--){int right=idx[nums[i]-1];ans+=(i-left[i])*(right-i);idx[nums[i]]=i;}return ans-n*(n+1)/2;
}最后不要忘记点赞,评论加收藏哦!!!