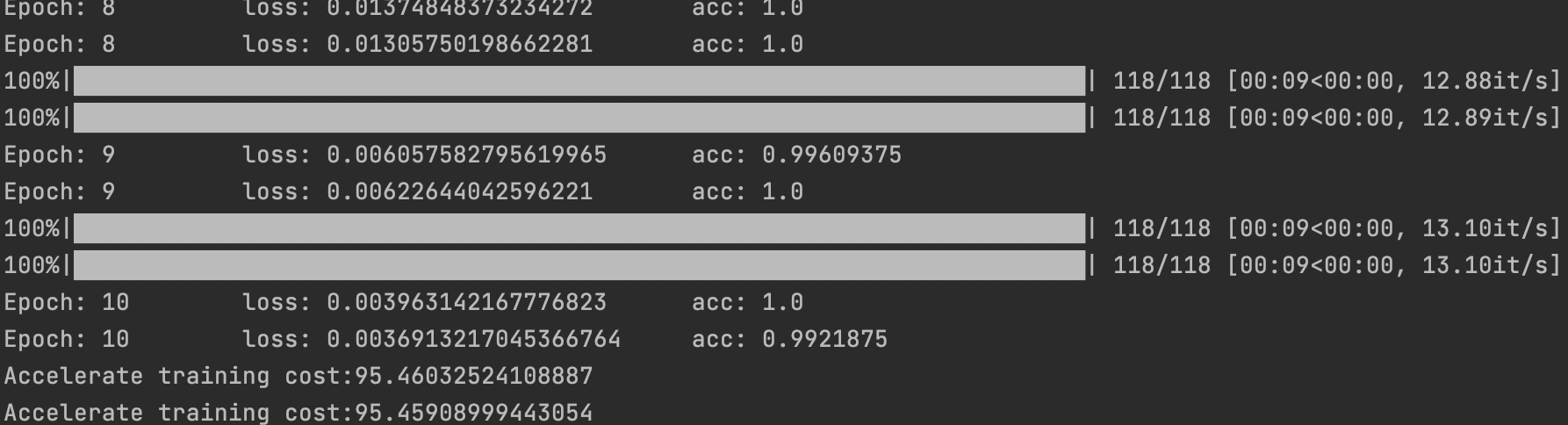
案例1 一阶线性插值
待加工零件外形根据工艺要求在一组数据(x,y)给定(如下表),用程控铣床加工时每一刀只能沿着x方向或y方向走非常小的一步,需要从已知数据得到加工步长很小的(x,y)的坐标。
下表中所给x,y数据位于机翼断面的下轮廓线上,假设需要得到x坐标改变值为0.1的y坐标,试完成加工所需数据,画出曲线,并求出x=0处曲线斜率和13≤x≤15范围内的y的最小值。
要求: (1)用分段线性插值法; (2)三次样条插值法.
插入点数据表
| x | 0 | 3 | 5 | 7 | 9 | 11 | 12 | 13 | 14 | 15 |
| y | 0 | 1.2 | 1.7 | 2.0 | 2.1 | 2.0 | 1.8 | 1.2 | 1.0 | 1.6 |
【符号设置】
- x0,y0 插入节点,即表1中已知数据;
- 待插数据,x=0:0.1:15;
- y 待插数据对应的纵坐标值;
- k0 表示x=0处的曲线斜率(即导数);
- Ymin 表示13≤x≤15范围内的y的最小值。
【数学模型1】线性插值公式
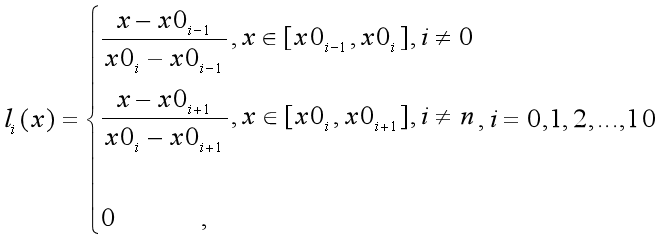

在x=0出的斜率的计算公式为
【模型1求解】
x0=[0 3 5 7 9 11 12 13 14 15];
y0=[0 1.2 1.7 2.0 2.1 2.0 1.8 1.2 1.0 1.6];
x=0:0.1:15;
y=interp1(x0,y0,x);
plot(x0,y0,'*',x,y,'+-')
dy=diff(y);
dx=diff(x);
dy_dx=dy./dx;
k0=dy_dx(1);
x1=x(x<=15&x>=13);
y1=y(x<=15&x>=13);
Ymin=min(y1);
yindex=find(y1==Ymin);
Xmin=x1(yindex);
[Xmin,Ymin,k0]
注:`dy = diff(y)` 是一个求解差分的函数,用于计算给定向量 y 的差分。
差分是指计算向量中相邻元素之间的差异。通过对 y 中的元素进行逐个相减,可以得到一个新的向量 dy,其长度比 y 少 1。换句话说,dy 中的每个元素都是 y 中相邻元素的差值。
差分常用于处理时间序列数据或离散数据,可以提供关于数据趋势、变化率和离散程度等方面的信息。通过计算差分,我们可以获得连续数据点之间的变化量,从而进行进一步的数据分析和处理。

根据计算,x=0处的斜率为k0=0.4;
当13<x<15时,y的最小值是Ymin=1,此时对应的横坐标为Xmin=14.
【数学模型2及其求解】三次样条插值
x0=[0 3 5 7 9 11 12 13 14 15];
y0=[0 1.2 1.7 2.0 2.1 2.0 1.8 1.2 1.0 1.6];
x=0:0.1:15;
y1=interp1(x0,y0,x,'spline');
pp1=csape(x0,y0);
y2=fnval(pp1,x);
pp2=csape(x0,y0,'second');
y3=fnval(pp2,x);
subplot(2,1,1);
plot(x,y1,'*-');
title('spline');
subplot(2,1,2);
plot(x,y3,'+-');
title('second');
dy=diff(y1);
dx=diff(x);
dy_dx=dy./dx;
k0=dy_dx(1);
yf=y1(131:end);
xf=x(131:end);
Ymin=min(yf);
Xmin=xf(yf==Ymin);
[Xmin,Ymin,k0]
注:`y1 = interp1(x0, y0, x, 'spline')` 和 `pp1 = csape(x0, y0)` 都是用于进行数据插值的函数,但是它们使用不同的插值方法和返回不同的结果。
`interp1` 函数使用的是插值方法中的样条插值,通过在已知数据点之间构建光滑的曲线来进行插值。在代码中,`'spline'` 是插值方法的参数,表示使用三次样条曲线进行插值。`interp1` 函数根据已知数据点 `(x0, y0)` 和待插值的自变量 `x`,计算对应的插值结果 `y1`。
`csape` 函数则使用的是样条插值的另一种形式,称为分段样条插值。它通过构建一组分段的三次多项式曲线来进行插值。在代码中,`csape` 函数的返回值 `pp1` 是一个样条插值对象,它包含了构建的分段样条曲线的相关信息。
相比较而言,`interp1` 函数使用起来更加简单,直接给出了插值结果。而 `csape` 函数则返回一个对象,需要进一步使用其他函数或方法来进行插值计算或求导等操作。使用 `csape` 函数可以更加灵活地控制插值过程,例如可以进行边界条件的设定或者选择不同的插值方法等。
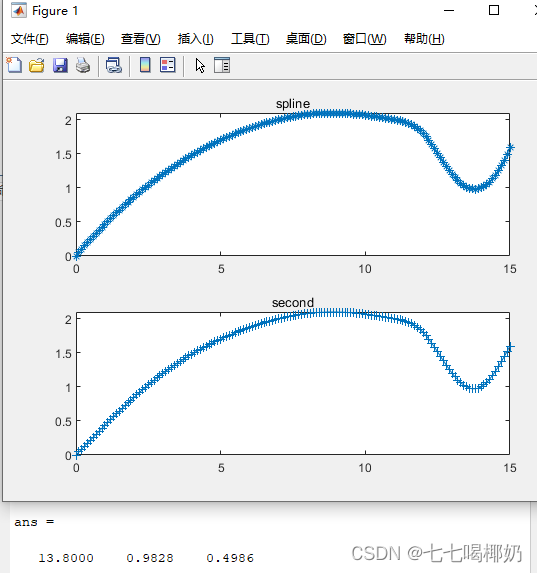
根据计算,x=0处的斜率为k0=0.4986;
当13<=x<=15时,y的最小值为Ymin=0.9828,对应的横坐标Xmin=13.8.
案例2 利用插值法求积分
已知速度曲线v(t)上的四个点数据,如下表,用三次样条插值求位移S(t)。
| t | 0.15 | 0.16 | 0.17 | 0.18 |
| V(t) | 3.5 | 1.5 | 2.5 | 2.8 |
【符号设置】
- T 时间;
- V 速度;
- S 位移(路程);
【数学模型】

其中,v(t)函数并不知道,只能靠四个节点插值生成。
【模型求解】
(1)利用三次样条插值,得到速度函数v(t)的表达式。
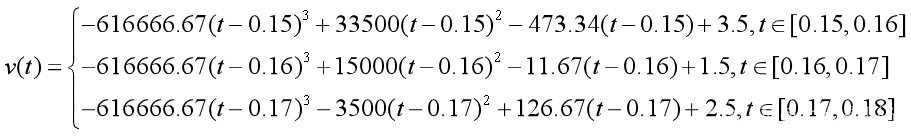
(2)求位移
 =0.068625
=0.068625