文章目录
- 竞赛链接
- Q1:7020. 统计对称整数的数目
- 竞赛时代码——枚举预处理
- Q2:8040. 生成特殊数字的最少操作(倒序遍历、贪心)
- 竞赛时代码——检查0、00、25、50、75
- Q3:2845. 统计趣味子数组的数目
- 竞赛时代码——前缀和+哈希表
- 相似题目——1590. 使数组和能被 P 整除(确实很相似的题目)
- Q4:2846. 边权重均等查询⭐⭐⭐⭐⭐
- 读题
- 解法——树上倍增、最近公共祖先LCA
- 相关题目
- 成绩记录
竞赛链接
https://leetcode.cn/contest/weekly-contest-361/
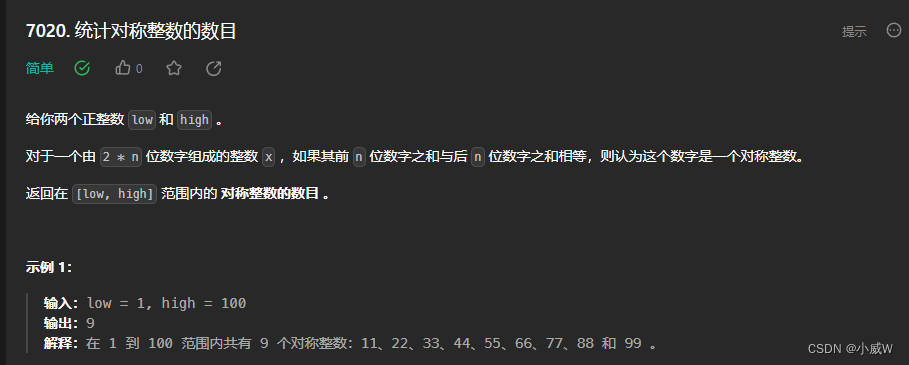
Q1:7020. 统计对称整数的数目
https://leetcode.cn/problems/count-symmetric-integers/
提示:
1 <= low <= high <= 10^4
竞赛时代码——枚举预处理
预处理所有数字是否为对称整数。
cnt[i]表示 <=i 的数字中有几个对称整数。
class Solution {static int[] cnt = new int[10005];// 预处理static {for (int i = 1; i <= 10001; ++i) {cnt[i] = cnt[i - 1];if (op(i)) cnt[i]++;}}public int countSymmetricIntegers(int low, int high) {return cnt[high] - cnt[low - 1];}// 判断x是否为对称整数public static boolean op(int x) {List<Integer> ls = new ArrayList<>();while (x != 0) {ls.add(x % 10);x /= 10;}int n = ls.size();if (n % 2 == 1) return false;int a = 0, b = 0;for (int i = 0; i < n; ++i) {if (i < n / 2) a += ls.get(i);else b += ls.get(i);}return a == b;}
}
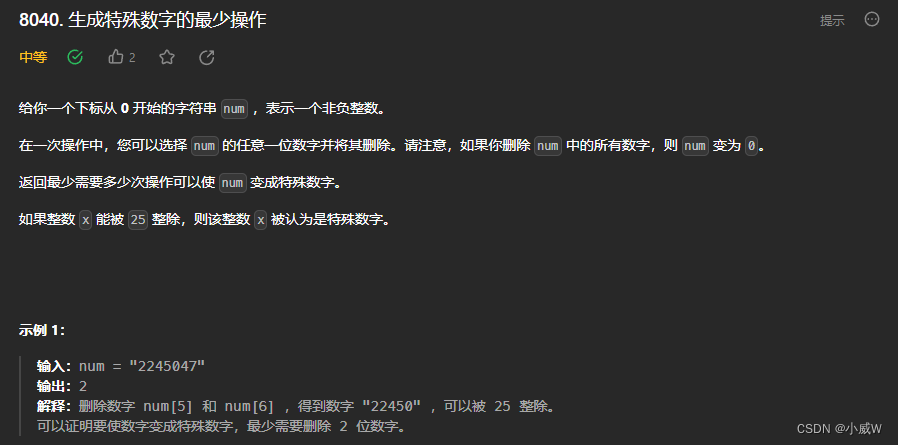
Q2:8040. 生成特殊数字的最少操作(倒序遍历、贪心)
https://leetcode.cn/problems/minimum-operations-to-make-a-special-number/
提示
1 <= num.length <= 100
num 仅由数字 '0' 到 '9' 组成
num 不含任何前导零
竞赛时代码——检查0、00、25、50、75
检查位置最靠后的 00、25、50、75 的位置。
如果都不存在但是有 0 的话,答案则为 n - 1。(因为 0 可以不删)
class Solution {public int minimumOperations(String num) {int n = num.length();boolean f0 = false, f5 = false;for (int i = n - 1; i >= 0; --i) {char ch = num.charAt(i);if (ch == '0') {if (f0) return n - i - 2; // 检查00f0 = true;} else if (ch == '5') {if (f0) return n - i - 2;; // 检查50f5 = true;} else if (ch == '2' || ch == '7') {if (f5) return n - i - 2;; // 检查25,75}}if (f0) return n - 1; // 检查是否有0return n;}
}
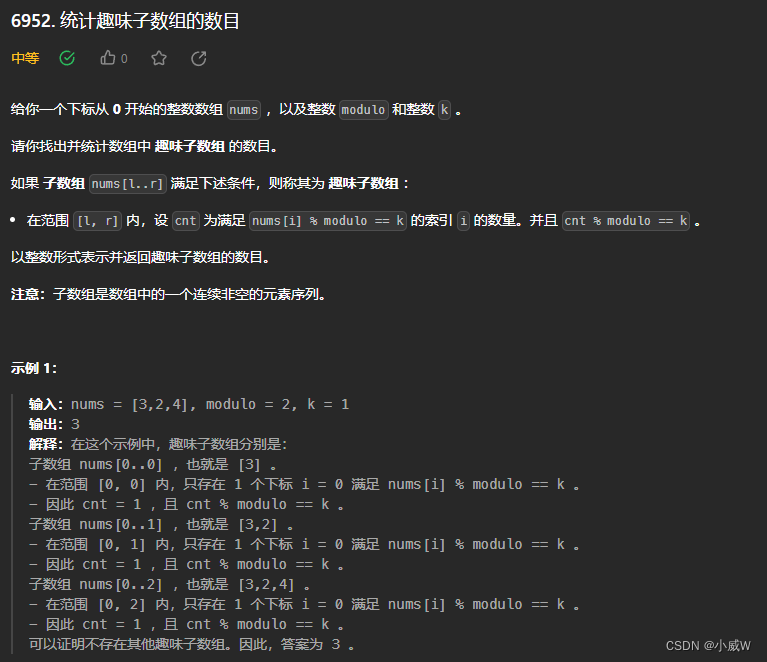
Q3:2845. 统计趣味子数组的数目
https://leetcode.cn/problems/count-of-interesting-subarrays/
提示:
1 <= nums.length <= 10^5
1 <= nums[i] <= 10^9
1 <= modulo <= 10^9
0 <= k < modulo
竞赛时代码——前缀和+哈希表
使用前缀和数组可以快速求出从 l ~ r 之间满足要求的元素个数 cnt。
求出前缀和数组之后,从前往后依次枚举下标。对于当前的前缀和 sum[r],前面有若干个满足 (sum[r] - sum[x]) % modulo == k 的下标,这些下标的共同特征是:它们的值 sum[x] = (sum[r] - k + modulo) % modulo。
在枚举的过程中用哈希表 cnt 记录下满组 sum[i] = y 的 i 的数量,就可以快速找到 r 之前有几个可以和当前下标配对的下标 l。
class Solution {public long countInterestingSubarrays(List<Integer> nums, int modulo, int k) {int n = nums.size();int[] x = new int[n], sum = new int[n + 1]; // x是原始数组,sum是前缀和数组Map<Integer, Integer> cnt = new HashMap<>(); // 存储各个余数为key的位置的数量cnt.put(0, 1);long ans = 0;for (int i = 0; i < n; ++i) {if (nums.get(i) % modulo == k) x[i] = 1;sum[i + 1] = (sum[i] + x[i]) % modulo; // 前缀和int r = sum[i + 1];ans += cnt.getOrDefault((r - k + modulo) % modulo, 0);cnt.merge(r, 1, Integer::sum);}return ans;}
}
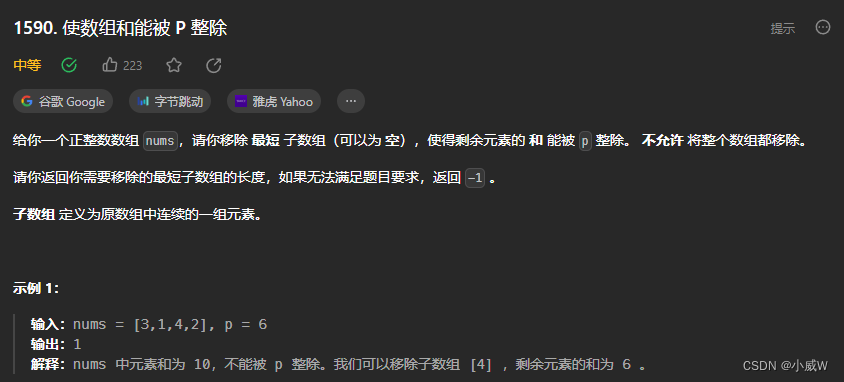
相似题目——1590. 使数组和能被 P 整除(确实很相似的题目)
https://leetcode.cn/problems/make-sum-divisible-by-p/description/
提示:
1 <= nums.length <= 105
1 <= nums[i] <= 109
1 <= p <= 109
class Solution {public int minSubarray(int[] nums, int p) {int n = nums.length;int[] sum = new int[n + 1]; // 前缀和数组for (int i = 0; i < n; ++i) {sum[i + 1] = (sum[i] + nums[i]) % p;}int t = sum[n], ans = n;if (t == 0) return 0;Map<Integer, Integer> idx = new HashMap<>(); // 记录各个前缀和出现的下标idx.put(0, -1);for (int i = 0; i < n; ++i) {// x是当前前缀和,y是和x配对组成t的前缀和int x = sum[i + 1], y = (x - t + p) % p; // 如果之前有y,就尝试更新答案 if (idx.containsKey(y)) ans = Math.min(ans, i - idx.get(y));idx.put(x, i);}return ans == n? -1: ans;}
}
Q4:2846. 边权重均等查询⭐⭐⭐⭐⭐
https://leetcode.cn/problems/minimum-edge-weight-equilibrium-queries-in-a-tree/
提示:
1 <= n <= 10^4
edges.length == n - 1
edges[i].length == 3
0 <= ui, vi < n
1 <= wi <= 26
生成的输入满足 edges 表示一棵有效的树
1 <= queries.length == m <= 2 * 10^4
queries[i].length == 2
0 <= ai, bi < n
读题
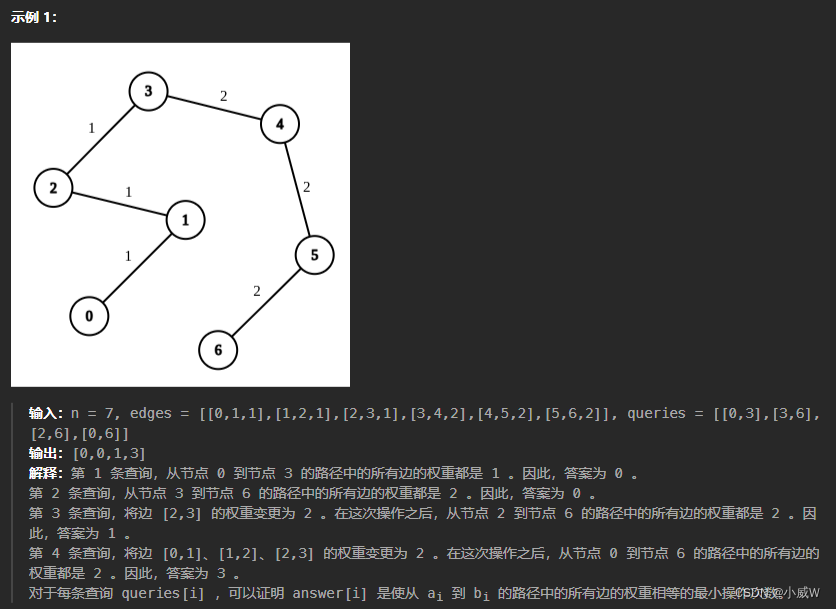
给了一个 n 个节点的无向图。
每次查询,给两个点 a ,b。求 a 和 b 路径之间的所有边权,都变成相等需要操作几步——实际上是求 a 和 b 之间有几条边,其中出现次数最多的边权出现了几次。
解法——树上倍增、最近公共祖先LCA
https://leetcode.cn/problems/minimum-edge-weight-equilibrium-queries-in-a-tree/solutions/2424060/lca-mo-ban-by-endlesscheng-j54b/

思路总结:
用树上倍增的思想维护:各个节点的深度、各个节点和父节点之间各种边权的数量。
求答案时,先将两个节点放在同一深度,实现方法是 y 先跳 d[y] - d[x] 的深度。
然后,x 和 y 一起往上跳。
class Solution {public int[] minOperationsQueries(int n, int[][] edges, int[][] queries) {// 临界表存储无向图List<int[]>[] g = new ArrayList[n]; Arrays.setAll(g, e -> new ArrayList<>());for (int[] e: edges) {int x = e[0], y = e[1], w = e[2] - 1;g[x].add(new int[]{y, w});g[y].add(new int[]{x, w});}int m = 32 - Integer.numberOfLeadingZeros(n); // n的二进制长度int[][] pa = new int[n][m]; // pa[x][i]表示节点x的第2^i个父节点for (int i = 0; i < n; ++i) {Arrays.fill(pa[i], -1); // -1表示没有这个父节点}int[][][] cnt = new int[n][m][26]; // cnt[x][i][w]记录节点x和父节点之间的边权为w的个数int[] depth = new int[n]; // 记录n个节点的深度// 使用 dfs 从0节点开始 初始化pa、cnt 计算depthdfs(0, -1, g, pa, cnt, depth);// 计算 pa 和 cnt// 先枚举i,(也就是先算出所有节点的爷爷、再求所有节点爷爷的爷爷...for (int i = 0; i < m - 1; ++i) { // 先枚举i,范围是0~m-2for (int x = 0; x < n; ++x) { // 再枚举xint p = pa[x][i]; // 取出节点x的第2^i个父节点if (p != -1) { int pp = pa[p][i]; // 取出节点x的第2^i个父节点的第2^i个父节点pa[x][i + 1] = pp; // 赋值——x的第2^(i+1)个父节点// 通过cnt[x][i]和cnt[p][i]计算 cnt[x][i+1]for (int j = 0; j < 26; ++j) {cnt[x][i + 1][j] = cnt[x][i][j] + cnt[p][i][j];}}}}// 计算答案int[] ans = new int[queries.length];for (int qi = 0; qi < queries.length; qi++) { // 枚举每一个查询int x = queries[qi][0], y = queries[qi][1];int pathLen = depth[x] + depth[y]; // x的深度和y的深度int[] cw = new int[26]; // 统计各种边权在x和y之间出现的次数// 让 x 作为深度更小的那个节点if (depth[x] > depth[y]) {int t = x;x = y;y = t;}// 让 y 和 x 在同一深度(先让 y 跳 depth[y]-depth[x])for (int k = depth[y] - depth[x]; k > 0; k &= k - 1) {int i = Integer.numberOfTrailingZeros(k);int p = pa[y][i];for (int j = 0; j < 26; ++j) {cw[j] += cnt[y][i][j];}y = p;}// y和x位于同一深度的时候可能位于同一个节点,那么就不用继续计算了if (y != x) {// 让 x 和 y 同时往上跳for (int i = m - 1; i >= 0; i--) { // 从大到小尝试各种2^i跳法int px = pa[x][i], py = pa[y][i];// 如果px!=py,说明可以跳if (px != py) {for (int j = 0; j < 26; ++j) {cw[j] += cnt[x][i][j] + cnt[y][i][j];} x = px;y = py;}}// 因为跳到最后,x和y都是最近公共祖先的直系节点,所以px一定会=py// 手动计算cnt[j]for (int j = 0; j < 26; ++j) {cw[j] += cnt[x][0][j] + cnt[y][0][j];}x = pa[x][0]; // x此时变成了 x 和 y 的最近公共祖先}int lca = x;pathLen -= depth[lca] * 2;int maxCw = 0;for (int i = 0; i < 26; ++i) maxCw = Math.max(maxCw, cw[i]);ans[qi] = pathLen - maxCw;}return ans;}public void dfs(int x, int fa, List<int[]>[] g, int[][] pa, int[][][] cnt, int[] depth) {pa[x][0] = fa; // 父节点for (int[] e: g[x]) { // 枚举和x相连的每一条边int y = e[0], w = e[1];if (y != fa) {cnt[y][0][w] = 1;depth[y] = depth[x] + 1;dfs(y, x, g, pa, cnt, depth);}}}
}
相关题目
1483. 树节点的第 K 个祖先
2836. 在传球游戏中最大化函数值
成绩记录

喜报!应该要升 guardian 了!