参考资料:
- 《机器学习2022》李宏毅
- 史上最详细循环神经网络讲解(RNN/LSTM/GRU) - 知乎 (zhihu.com)
- LSTM如何来避免梯度弥散和梯度爆炸? - 知乎 (zhihu.com)
1 RNN 的结构
首先考虑这样一个 slot filling 问题:
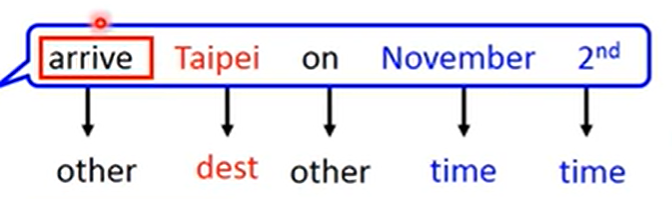
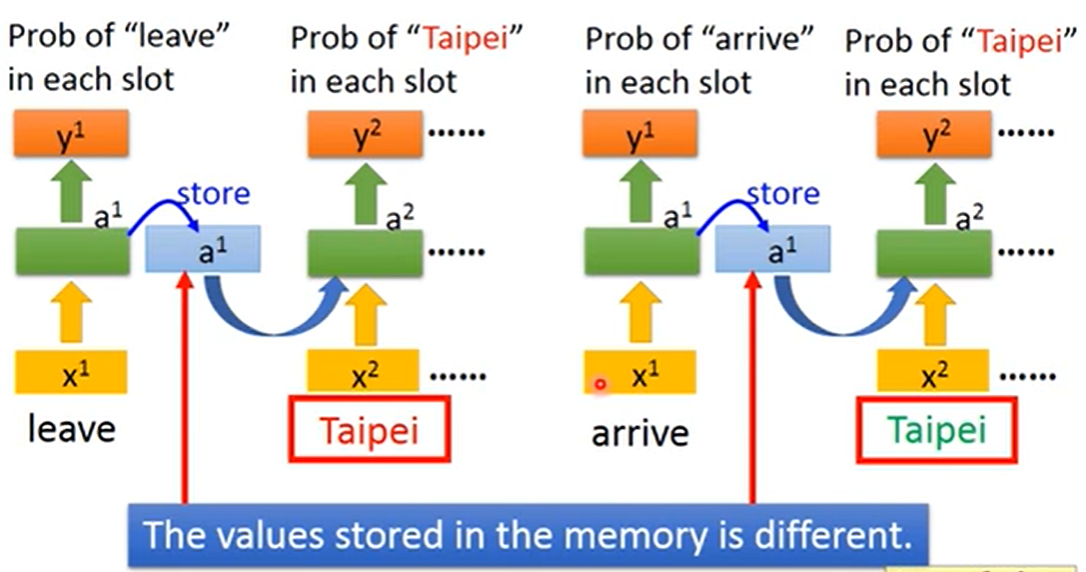
注意到,上图中 Taipei 的输出为 destination。如果我们只是单纯地将每个词向量输入到一个神经网络中,那么对于"leave Taipei on …" 这句话,模型对 Taipei 的输出也会是 destination,但我们希望它是 departure。要实现这一目的,必须要引入当前向量与上下文的关系,于是就有了循环神经网络(RNN):
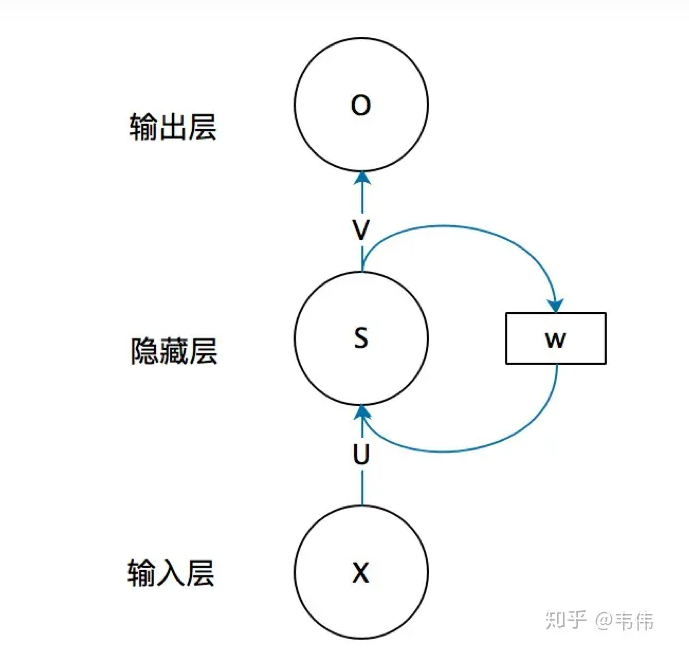
注意到,RNN 与一般的神经网络的主要区别在与将隐层的上一次输出保存并作为本次的输入,即:
O t = g ( V ⋅ S t ) S t = f ( U ⋅ X t + W ⋅ S t − 1 ) \begin{align} O_t&=g(V\cdot S_t)\notag\\ S_t&=f(U\cdot X_t+W\cdot S_{t-1})\notag \end{align} OtSt=g(V⋅St)=f(U⋅Xt+W⋅St−1)
矩阵 U , W , V U,W,V U,W,V 即为 RNN 的参数,与 t t t 无关。
引入时间这一维度,RNN 可以表示为如下结构:
如果采用双向 RNN ,则每个向量都可以充分地考虑到上下文。
2 RNN 的梯度消失与梯度爆炸
考虑这样一个简单的 RNN 结构:
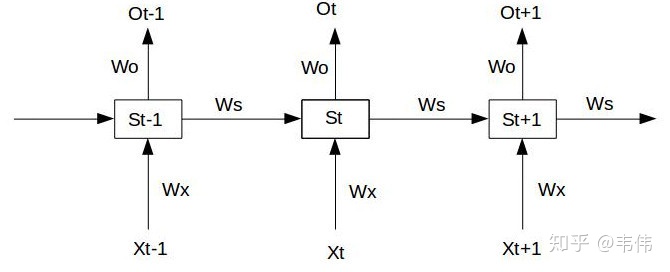
假设神经元没有激活函数(激活函数的导数一般是恒 < 1 <1 <1 的),则有:
S 1 = W x X 1 + W s S 0 + b 1 O 1 = W o S 1 + b 2 S 2 = W x X 2 + W s S 1 + b 1 O 2 = W o S 2 + b 2 S 3 = W x X 3 + W s S 2 + b 1 O 3 = W o S 3 + b 2 \begin{align} S_1&=W_xX_1+W_sS_0+b_1\quad&O_1=W_oS_1+b_2\notag\\ S_2&=W_xX_2+W_sS_1+b_1\quad&O_2=W_oS_2+b_2\notag\\ S_3&=W_xX_3+W_sS_2+b_1\quad&O_3=W_oS_3+b_2\notag\\ \end{align} S1S2S3=WxX1+WsS0+b1=WxX2+WsS1+b1=WxX3+WsS2+b1O1=WoS1+b2O2=WoS2+b2O3=WoS3+b2
设 t 3 t_3 t3 时刻的损失函数为 L 3 L_3 L3 ,则有:
∂ L 3 ∂ W o = ∂ L 3 ∂ O 3 ∂ O 3 ∂ W o ∂ L 3 ∂ W x = ∂ L 3 ∂ O 3 ∂ O 3 ∂ S 3 ( X 3 + W s ( X 2 + W s X 1 ) ) ∂ L 3 ∂ W s = ∂ L 3 ∂ O 3 ∂ O 3 ∂ S 3 ( S 2 + W s ( S 1 + W s S 0 ) ) \begin{align} \frac{\partial L_3}{\partial W_o}&=\frac{\partial L_3}{\partial O_3}\frac{\partial O_3}{\partial W_o}\notag\\ \frac{\partial L_3}{\partial W_x}&=\frac{\partial L_3}{\partial O_3}\frac{\partial O_3}{\partial S_3}\bigg(X_3+W_s\Big(X_2+W_sX_1\Big)\bigg)\notag\\ \frac{\partial L_3}{\partial W_s}&=\frac{\partial L_3}{\partial O_3}\frac{\partial O_3}{\partial S_3}\bigg(S_2+W_s\Big(S_1+W_sS_0\Big)\bigg)\notag\\ \end{align} ∂Wo∂L3∂Wx∂L3∂Ws∂L3=∂O3∂L3∂Wo∂O3=∂O3∂L3∂S3∂O3(X3+Ws(X2+WsX1))=∂O3∂L3∂S3∂O3(S2+Ws(S1+WsS0))
这部分的公式和参考资料里的不太一样,但我感觉参考资料里的公式不太严格吧?
所以,任意时刻损失函数对 W x , W s W_x,W_s Wx,Ws 的偏导为:
∂ L t ∂ W x = ∂ L 3 ∂ O 3 ∂ O 3 ∂ S 3 ∑ k = 1 t W s t − k X k ∂ L t ∂ W s = ∂ L 3 ∂ O 3 ∂ O 3 ∂ S 3 ∑ k = 1 t W s t − k S k − 1 \begin{align} \frac{\partial L_t}{\partial W_x}&=\frac{\partial L_3}{\partial O_3}\frac{\partial O_3}{\partial S_3}\sum\limits_{k=1}^{t}W_s^{t-k}X_k\notag\\ \frac{\partial L_t}{\partial W_s}&=\frac{\partial L_3}{\partial O_3}\frac{\partial O_3}{\partial S_3}\sum\limits_{k=1}^{t}W_s^{t-k}S_{k-1}\notag\\ \end{align} ∂Wx∂Lt∂Ws∂Lt=∂O3∂L3∂S3∂O3k=1∑tWst−kXk=∂O3∂L3∂S3∂O3k=1∑tWst−kSk−1
当 W s ∈ ( 0 , 1 ) W_s\in(0,1) Ws∈(0,1) 时,损失函数对 W x , W s W_x,W_s Wx,Ws 的偏导会逐渐“遗忘”距离较远的梯度,所以模型很难学习到距离较远的依赖关系。
当 W s > 1 W_s>1 Ws>1 时,前面的梯度对当前的影响会随着距离增加而指数级增大,甚至变成 NaN.
3 LSTM
LSTM(Long Short-term Memory) 是 RNN 的变体,并且已经逐渐成为了 RNN 的代名词,其基本结构如下图所示:
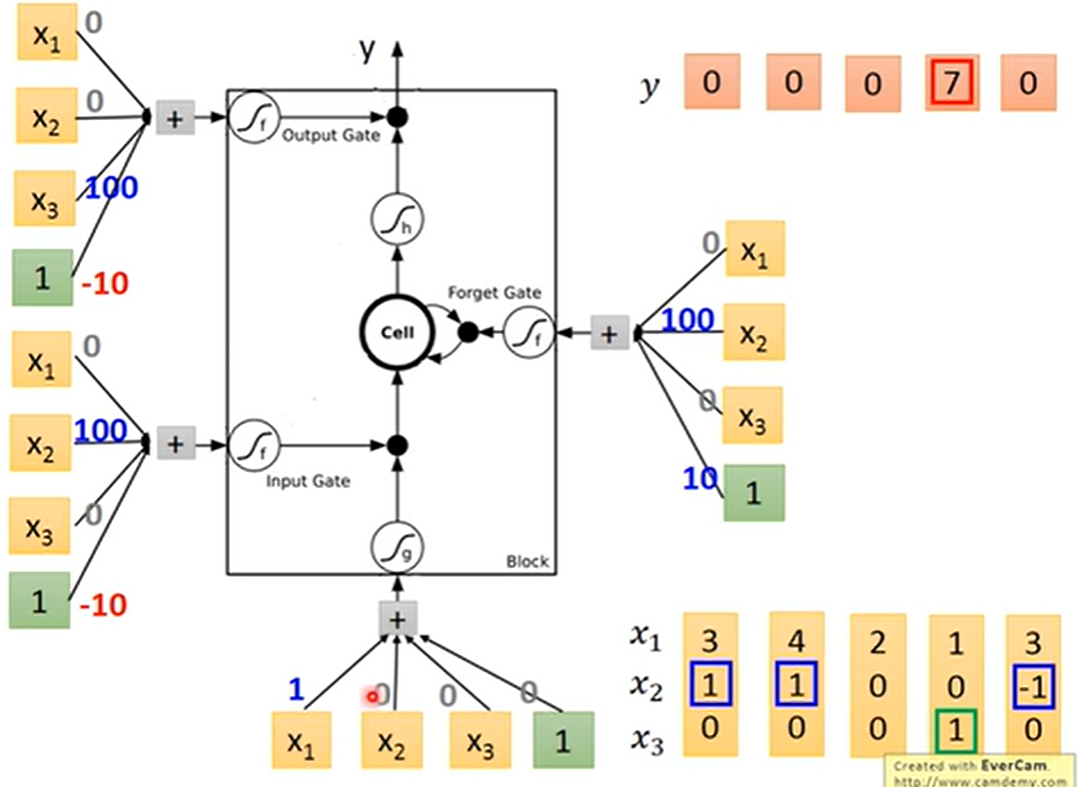
相比普通的 RNN ,LSTM增加了输入门、输出门和遗忘门。
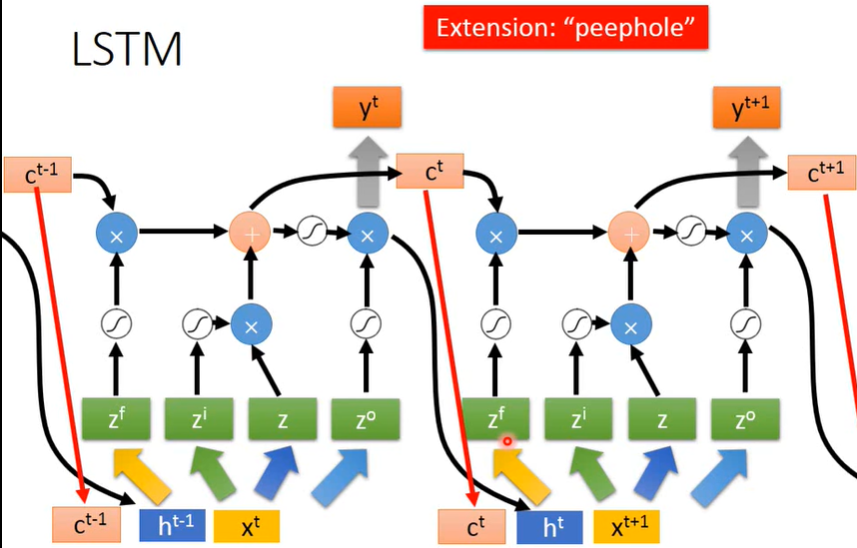
上图中, z f , z i , z , z o z_f,z_i,z,z_o zf,zi,z,zo 均有相应的权值矩阵乘上拼接后的输入向量得到。
LSTM 可以解决 RNN 梯度消失的问题,因为如果不考虑遗忘门,距离再远的梯度也可以通过 c i → ⋯ → c t − 1 → c t c_{i}\rightarrow\cdots\rightarrow c_{t-1}\rightarrow c_t ci→⋯→ct−1→ct 这条路径无损地传递到到当前的梯度。