数学表达

一阶多智能体的运动学方程可以描述为
x ˙ i ( t ) = u i ( t ) , i ∈ { 1 , 2 , 3 , … , N } \dot x_i(t) = u_i(t),i\in\{1,2,3,\dots,N\} x˙i​(t)=ui​(t),i∈{1,2,3,…,N}
其中$x_i(t)$为状态，$u_i(t)$为控制量，最终期望的结果为
$$\underset{t\to T}{\lim }|x_i(t)-x_j(t)|=0$$

$$|x_i(t)-x_j(t)|=0,\forall t\ge T$$

其中上式中第一个等式表示在时间趋近于$T$的时候，智能体的状态趋于一致。第二个等式表示在时间超过$T$的时候智能体的时间已经保持一致。

将一阶多智能体的一致性算法表示为
$$u_i(t)=-\sum _{j=1}^N{a}_{ij}(x_i(t)-x_j(t))$$
这里有一个小技巧，如果用矩阵的形式表示的话，那么直接使用拉普拉斯矩阵表示
$$u(t)=-x(t)\cdot L$$

仿真

设置智能体的初始状态为
$$x=\left[\begin{array}{cccc}1& 2& 3& 4\end{array}\right]$$
智能体的连接为

智能体1 --- 智能体2|          ||          | 
智能体4 --- 智能体3

那么拉普拉斯矩阵为
$$L=\left[\begin{array}{cccc}2& -1& 0& -1\\ -1& 2& -1& 0\\ 0& -1& 2& -1\\ -1& 0& -1& 2\end{array}\right]$$
仿真代码为(matlab)

clc;clear;closex = [1 2 3 4];
u = [];
A = [0 1 0 1;1 0 1 0;0 1 0 1;1 0 1 0;];
B = [2 0 0 0;0 2 0 0;0 0 2 0;0 0 0 2;];
L = B - A;
dt = 0.001;
k = 3;
lambda = 2;
mu = 0.1;for i = 1:4000u1 = -x(end,:) * L;x1 = x(end,:) + u1 * dt;u = [u;u1];x = [x;x1];
end

画出控制量的曲线以及状态量曲线

Fig1 = figure(1);
plot(0.001:0.001:4.001,x,'LineWidth', 1.5);
xlabel('t');
ylabel('x');
legend('agent1','agent2','agent3','agent4');
print(Fig1,'x','-dpng','-r600')Fig2 = figure(2);
plot(0.001:0.001:4.000,u,'LineWidth', 1.5);
xlabel('t');
ylabel('u');
legend('agent1','agent2','agent3','agent4');
print(Fig2,'u','-dpng','-r600')

状态变量的随时间变化图为

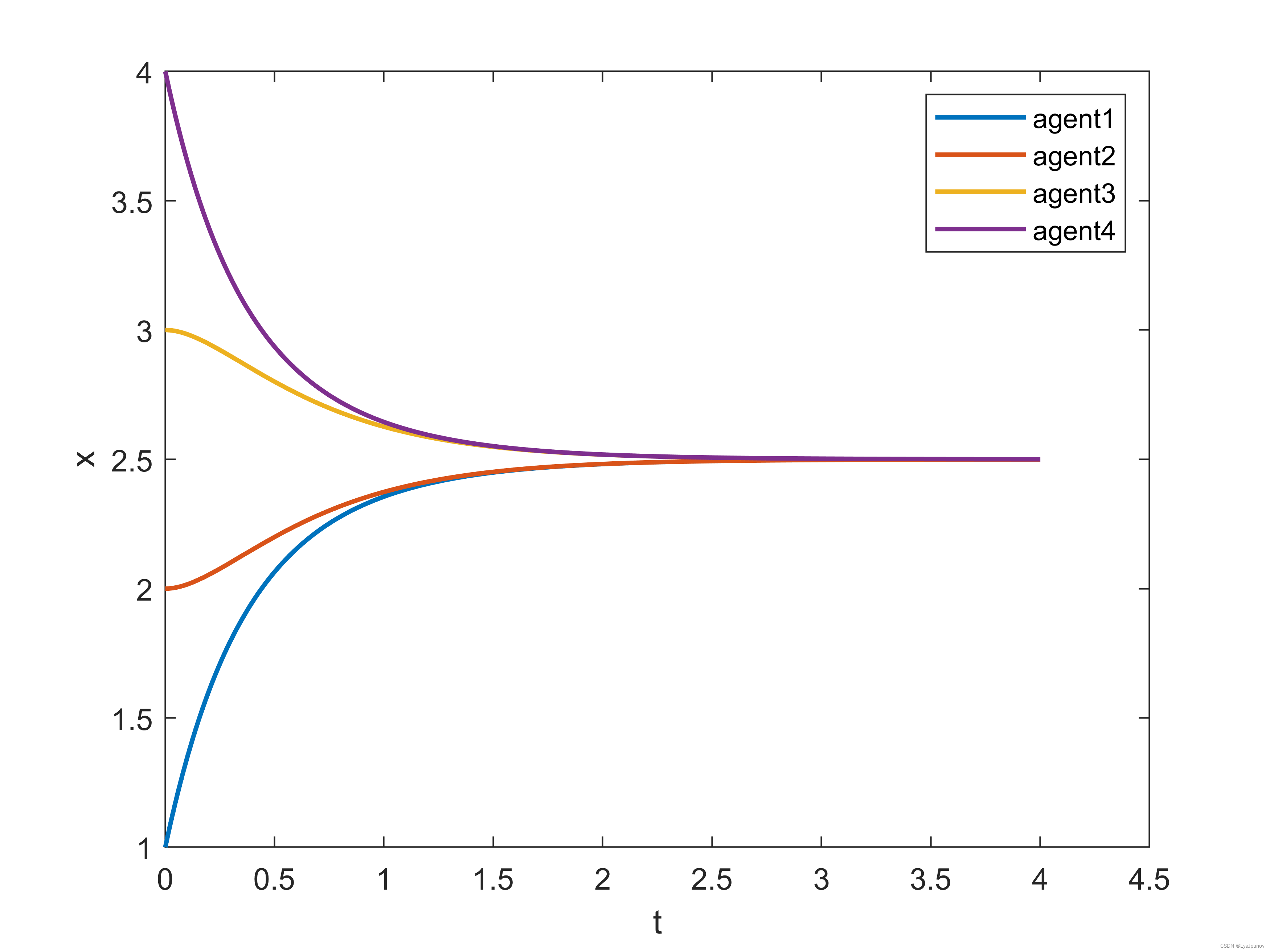
控制量随时间变化图为

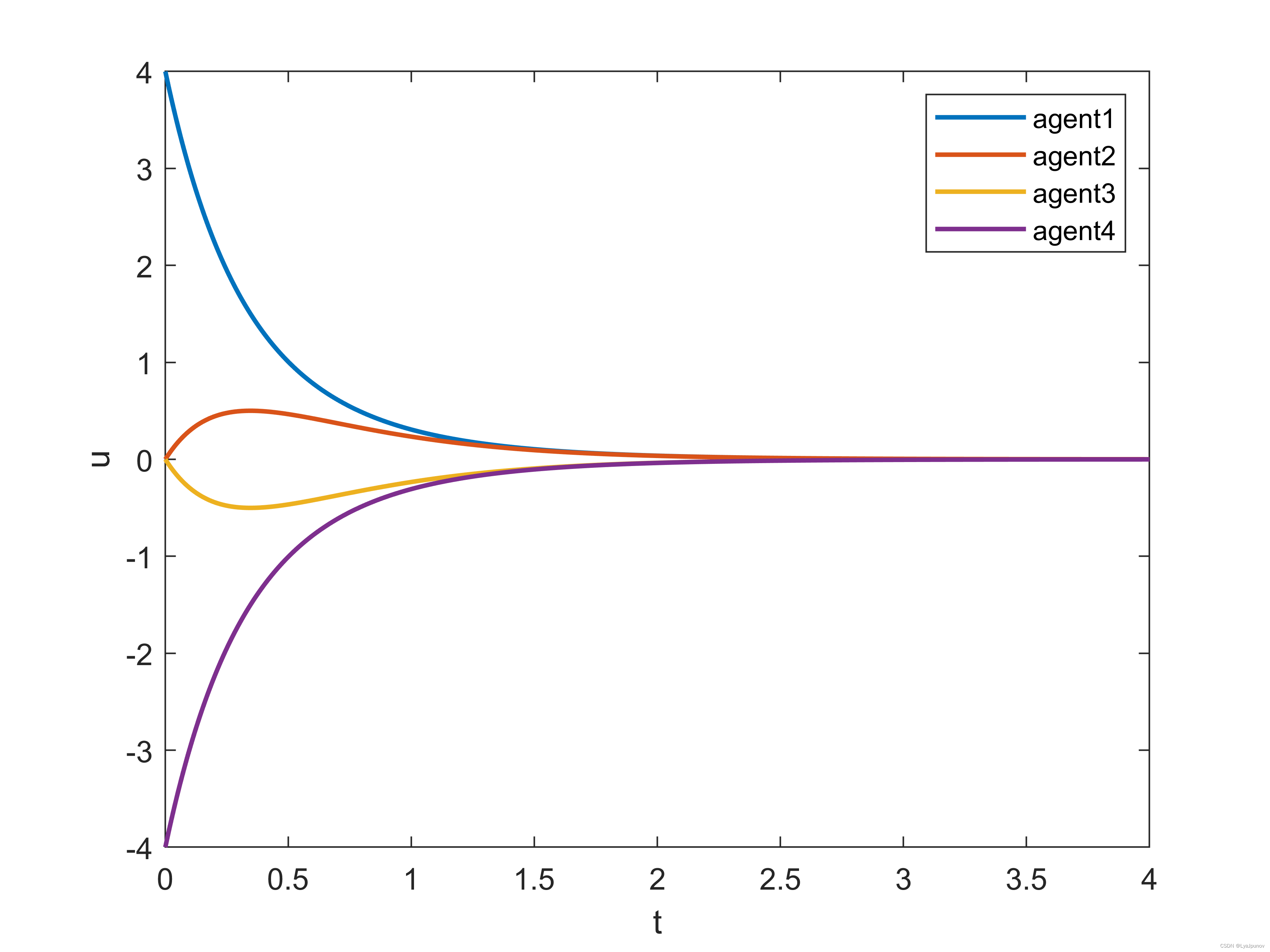
可以看到，最终四个智能体的状态全部归于一致。