题目列表
2833. 距离原点最远的点
2834. 找出美丽数组的最小和
2835. 使子序列的和等于目标的最少操作次数
2836. 在传球游戏中最大化函数值
一、距离原点最远的点

这题主要是理解题意,遇到'L'往左走,遇到'R'往右走,遇到'_'左右都可以走,题目问移动完成后,距离原点的最长距离,这很显然,只有所有的‘_’都往一个方向走的时候,才是最大的
代码如下
class Solution {
public:int furthestDistanceFromOrigin(string moves) {int ret=0,l=0;for(int i=0;i<moves.size();i++){if(moves[i]=='L') l++;else if(moves[i]=='R') l--;else ret++;}ret+=abs(l);return ret;}
};二、找出美丽数组的最小和
这题和359周赛的第二题一样,就不再写了,贴个代码
class Solution {
public:long long minimumPossibleSum(int n, int target) {long long m=min(target/2,n);return m*(m+1)/2+(target+target+(n-m-1))*(n-m)/2;}
};三、使子序列的和等于目标的最小操作次数
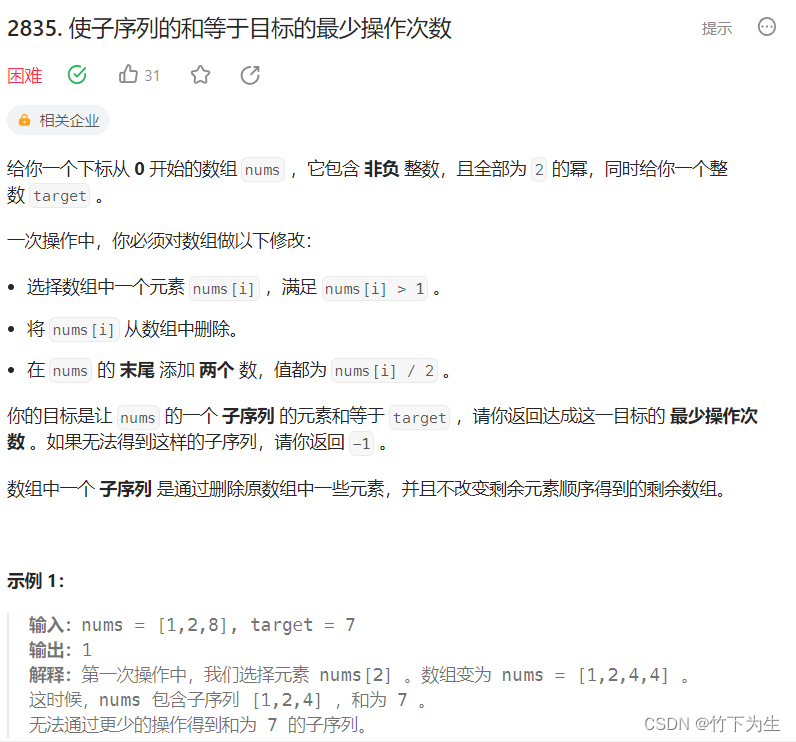
这题思路在于,题目给的数组存放的是2的幂,我们要想到数的二进制表示,从而想到用nums中的数据来凑出target的每一个二进制位上的1。
而target的每一个二进制上的1,有三个来源:
1.数组本身就有
2.用<2^i的数凑出一个2^i
3.将大于2^i的数拆分成我们需要的2^i
而题目要求我们返回最少的操作次数,那么我们肯定优先前两个方案,尽量避免拆分,所以我们将nums数组排序,并且从低位开始枚举target的二进制位上的1
方案一和方案二可以合并成:用<=2^i的数字凑出2^i
首先我们明确<=2^i的各个数字之和一定>=2^i才有可能凑出2^i,接下来,我们用数学归纳法进行证明用<=2^i的数子之和>=2^i的这些数一定能凑出2^i,s代表<=2^i的数字之和
当i=1,s>=2时,用<=2的数凑出2
1)如果存在2,很显然直接得到2
2)如果不存在2,那么<2^1的数字只能是1,而1相加很显然能得到2^1
所以,<=2^1的数字之和>=2^1的这些数一定能凑出2^1
当i=2,s>=4时,用<=4的数凑出4
1)如果存在4,显然能得到4
2)如果不存在4,<4的数字只能是1/2,即<=2^1,且s>=4>=2,所以根据上面的结论,得到一个2,剩下s-2>=2,同理,还能得到一个2,两个2相加得到4
所以,<=2^2的数字之和>=2^2的这些数一定能凑出2^2
当i=3,s>=8时,用<=8的数凑出8
1)如果存在8,显然能得到8
2)如果不存在8,<8的数字只能是1/2/4,即<=2^2,且s>=8>=4,所以根据上面的结论,得到一个4,剩下s-4>=4,同理,还能得到一个4,两个4相加得到8
所以,<=2^3的数字之和>=2^3的这些数一定能凑出2^3
综上所诉,一直这样推到下去就会得到:用<=2^i的数子之和>=2^i的这些数一定能凑出2^i
方案三:根据题目要求,我们选择数组中离2^i最近的2^j (j>i) 进行拆分,这样操作次数最少,而我们很容易知道,一旦差分了2^j,那么2^(i+1),2^(i+2),...,2^(j-1)就都不用考虑了,因为在拆分2^j时,已经得到了这些数,拆分的次数为 j-i (可以找个例子看看)
那么这题什么时候返回-1,我们知道任何一个2的幂都能被拆成1,所以只有数组之和小于target时,才会返回-1
技巧:当我们在凑出2^i之后,原本的算法应该是需要减去2^i,再去看剩下的数能不能凑出下一个2^i,但是我们也可以只加不减,只要我们在比较时,连同target的二进制i位之前的位数一起比较
代码如下
class Solution {
public:int minOperations(vector<int>& nums, int target) {//返回-1的情况if(accumulate(nums.begin(),nums.end(),0LL)<target)return -1;//记录每一位二级制1的个数long long cnt[32]={0};for(auto&x:nums)cnt[__builtin_ctz(x)]++;//__builtin_ctz得到最右边二进制位1的位数int i=0,ret=0;long long sum=0;while(target>=(1u<<i)){sum+=cnt[i]<<i;int mask=(1u<<(i+1))-1;//小技巧if(sum>=(mask&target)){//能凑出来i++;continue;}//需要拆分i++,ret++;while(cnt[i]==0)i++,ret++;}return ret;}
};四、在传球游戏中最大化函数值
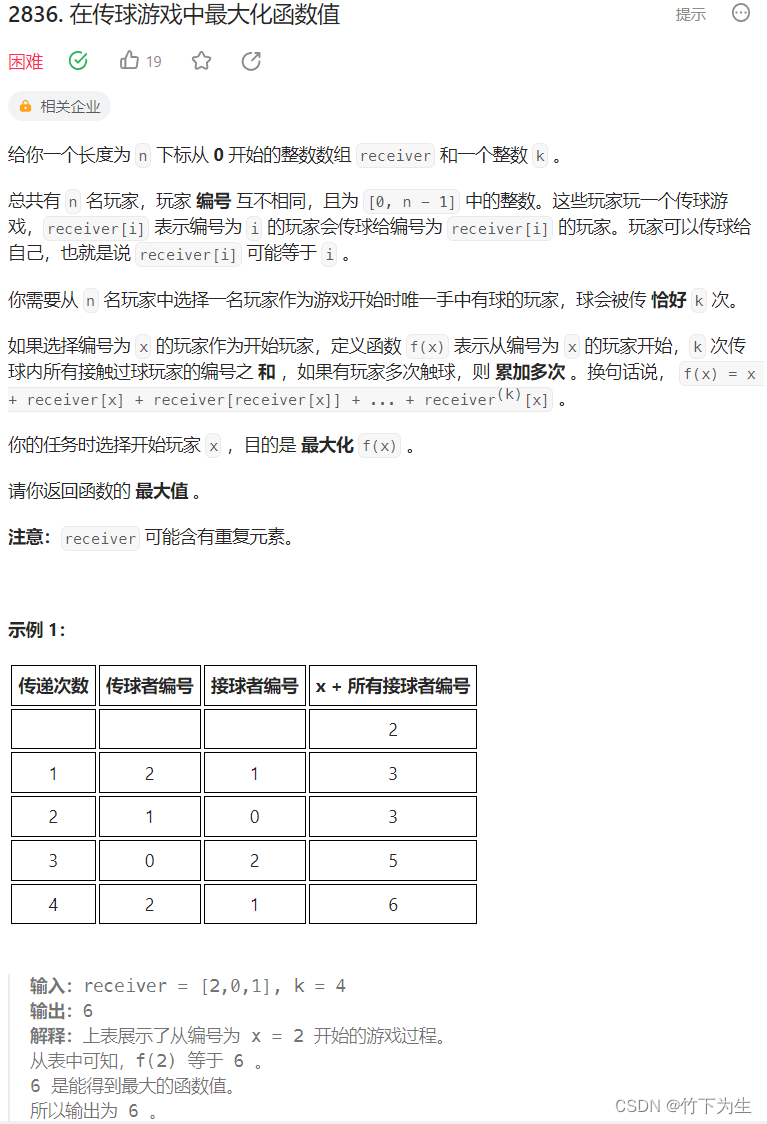
这题题目看起来很复杂,但是其实就是让你求传k次球之后得到的最大下标和,如果直接暴力,这题的数据范围肯定会超时,所以这题就是让我们优化时间复杂度,
这里要提到一个倍增的算法思想,本质就是预处理记录每个球员传2^i次球后的得分和接到球的人的下标(这里用x^i都无所谓,只是2^i比较好计算),根据数据范围可以知道,这样每个人的求解时间都在O(logk)以内,时间复杂度为O(nlogk)
代码如下
class Solution {
public:long long getMaxFunctionValue(vector<int>& receiver, long long k) {int n=receiver.size();int m=64 - __builtin_clzll(k);//k的二进制长度int g[n][m+1];//记录2^i后的接球人的下标long long f[n][m+1];//记录2^i后得到的下标和for(int i=0;i<n;i++)//初始化f[i][0]=g[i][0]=receiver[i];//预处理for(int i=1;i<m+1;i++){for(int j=0;j<n;j++){g[j][i]=g[g[j][i-1]][i-1];f[j][i]=f[j][i-1]+f[g[j][i-1]][i-1];}}long long ans=0;for(int i=0;i<n;i++){long long res=i;for(int j=0,node=i;j<m+1;j++){if((k>>j)&1){res+=f[node][j];node=g[node][j];} }ans=max(ans,res);}return ans;}
};![java八股文面试[数据库]——最左匹配原则](https://img-blog.csdnimg.cn/cacf87d4af5e4229a59857283e063b7d.png)