| 地图投影 | 示例 | 说明 |
|---|---|---|
| 亚当斯方形 II |  | 该投影以方形显示世界。该投影为等角投影,但方形的四个角除外。 |
| 埃托夫 | 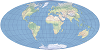 | 该折衷改进的方位投影采用椭圆的形式。该投影主要用于世界地图。 |
| 阿尔伯斯 |  | 该等积圆锥投影最适合用于中纬度东西方向分布的大陆板块。 |
| 方位自适应圆柱 |  | 该折衷的地图投影将纬线调整为画布的高度与宽度之比(纵横比)。纵横比必须介于 0.3 到 1 之间。 |
| 等距方位 |  | 该投影保留距中心点的距离和方向。该投影主要用于半球地图。 |
| 贝尔曼 | 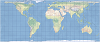 | 该投影为标准纬线位于南北纬 30° 的圆柱等积投影。 |
| 柏哥斯星状 |  | 这种不连续的投影采用星形的形式,美国地理学家协会 (AAG) 在其徽标中使用该投影。 |
| 彭纳 | 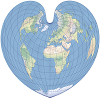 | 该等积投影在历史上曾用于绘制各大洲的地图。其经纬网采用心形的形式。 |
| 卡西尼 |  | 该横轴圆柱等距投影适用于主要南北分布的大比例地图。 |
| 紧凑型米勒 |  | 与米勒投影相比,该折衷的圆柱世界地图投影会压缩两极区域。 |
| 克拉斯特抛物线 | 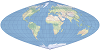 | 此伪圆柱等积投影主要用于绘制世界专题地图。 |
| 立方体 | 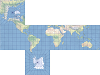 | 这是一个分面投影,由可折叠成立方体的六个正方形面组成。 |
| 圆柱等积 |  | 该投影保持地图上的相对面积,并以矩形呈现世界。 |
| 双立体 | 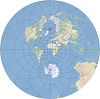 | 该方位投影为等角投影,并将用于新不伦瑞克和荷兰的大比例坐标系。 |
| 埃克特 I |  | 该折衷的伪圆柱投影主要用作新式地图。 |
| 埃克特 II |  | 该等积伪圆柱投影主要用作新式地图。 |
| 埃克特 III |  | 该折衷的伪圆柱地图投影用于绘制通用世界地图。 |
| 埃克特 IV |  | 该等积伪圆柱地图投影通常用于要求面积精确的专题和其他世界地图。 |
| 埃克特 V |  | 该折衷的伪圆柱地图投影用于绘制通用世界地图。 |
| 埃克特 VI |  | 此等积投影主要用于专题世界地图。 |
| 埃克特-格里芬多夫 | 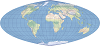 | 该等积投影是兰勃特方位等积投影的改进投影。 |
| 平等地球 | 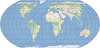 | 该等积伪圆柱投影对于陆地特征具有令人满意的外观,适用于专题世界地图。 |
| 等距圆锥 | 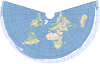 | 该圆锥投影保留沿所有经线和两条标准纬线的距离,最适合用于中纬度东西分布的区域。 |
| 等距圆柱 |  | 该投影形成等积矩形格网。也称作等矩形、简单圆柱、矩形和简易圆柱投影。 |
| 富勒 | 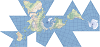 | 该投影是展开的 20 面二十面体,保持陆地板块不间断。 |
| 高尔立体投影 |  | 该透视圆柱地图投影的两条标准纬线位于北纬 45° 和南纬 45°,并放大了极点区域。 |
| 高斯-克吕格 | 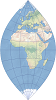 | 该投影称作椭圆体版本的横轴墨卡托投影。它是等角投影,不会保持真实的方向,适用于绘制大比例或较小区域地图。 |
| 对地静止卫星 |  | 此投影由对地静止卫星使用,用于返回通过卫星扫描角度定位的数据。 |
| 球心 |  | 此方位投影将地心作为透视点。它将大圆投影为直线。 |
| 古蒂等面积 |  | 该等面积伪圆柱投影是摩尔维特和正弦投影的组合,最常以不连续形式使用。 |
| 汉麦尔 | 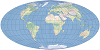 | 该投影是兰勃特方位等积投影的改进投影。该投影也称作汉麦尔-埃托夫投影。 |
| 洪特尼斜轴墨卡托 | 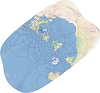 | 这是由 Martin Hotine 开发的斜轴墨卡托投影。该投影用于对既不朝南北方向也不朝东西方向,而是斜向延伸的区域进行等角制图。 |
| IGAC 平面笛卡尔 |  | 该投影用于绘制哥伦比亚城市地图。该投影仅支持非常大的比例。 |
| Krovak |  | 该投影是一种斜轴兰勃特等角圆锥投影,专为前捷克斯洛伐克设计。该投影用于对既不朝南北方向也不朝东西方向,而是斜向延伸的区域进行制图。 |
| 拉伯得斜轴墨卡托 | 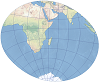 | 这是由 Jean Laborde 开发的斜轴墨卡托投影。该投影用于对既不朝南北方向也不朝东西方向,而是斜向延伸的区域进行等角制图。 |
| 兰勃特方位等积 |  | 该投影将保留大陆要素的真实相对大小。最适合用于专题半球地图和专题极点区域地图。 |
| 兰勃特等角圆锥 | 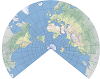 | 该等角圆锥投影最适合用于中纬度东西方向分布的大陆板块。 |
| Local |  | 这是一种专用地图投影,不考虑地球的曲率,适用于极大比例下的局部坐标系。 |
| Loximuthal | 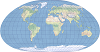 | 此投影将等角航线或恒向线显示为直线,从中央经线和中央纬线的交点开始,方位角和比例都是正确的。 |
| 麦克布赖德-托马斯平极四次 | 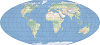 | 此等积投影主要用于专题世界地图。 |
| 墨卡托 |  | 最初设计等角圆柱投影的目的是为了显示精确罗盘方位,为海上航行提供保障。此投影的一个功能是能够以最小比例精确显示所有局部形状和角度。 |
| 米勒圆柱 | 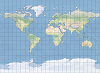 | 此投影与墨卡托投影类似,只是极点区域的面积畸变不如后者大。 |
| 摩尔维特 |  | 该等积伪圆柱投影用于以椭圆的形式显示世界,轴采用 2:1 比率。该投影适用于小比例专题地图。 |
| 自然地球 | 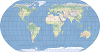 | 该折衷的伪圆柱地图投影用于绘制世界地图。该投影是为显示物理数据而专门设计的。 |
| 自然地球 II | 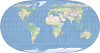 | 该折衷的伪圆柱地图投影用于绘制经线突显的世界地图,这些经线向极点急剧弯曲。 |
| 新西兰国家格网 |  | 此投影是一种用于新西兰大比例地图的标准投影。 |
| 改进的兰勃特等角锥投影 |  | 这是改进的兰伯特等角圆锥投影,用于对于极点附近的区域进行制图。 |
| 正射 |  | 此透视投影从无穷远处观察地球。这样便可提供地球的三维图像。 |
| 帕特森 |  | 该折衷的圆柱地图投影由 Tom Patterson 于 2014 年设计。 |
| 皮尔斯梅花 |  | 该投影以方形显示世界。该投影为等角投影,但方形的四条边的中点除外。 |
| 透视圆柱 |  | 这是能够以几何方式构造的圆柱地图投影。中央圆柱投影属于一种特殊情况。 |
| 简易圆柱 |  | 此投影易于构造,因为它可形成等方形格网。该投影通常用于以地理坐标系显示数据。 |
| 多圆锥 |  | 此投影的名称可理解为“许多圆锥”,也指出了投影方法。 |
| 四次等积 |  | 此伪圆柱等积投影主要用于绘制世界专题地图。 |
| 改良斜正形 |  | 这是由 Martin Hotine 开发的斜轴墨卡托投影。该投影用于对既不朝南北方向也不朝东西方向,而是斜向延伸的区域进行等角制图。其用于马来西亚和文莱。 |
| 罗宾森 |  | 此投影是一种用于世界地图的折衷投影。 |
| 正弦曲线 |  | 该伪圆柱等积投影以真实比例显示所有纬线和中央经线。 |
| 立体 |  | 此方位投影为等角投影。 |
| 乘 | 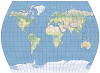 | 该折衷的伪圆柱地图投影是经过改良的高尔立体投影,但是经线是弯曲的。 |
| 托布勒圆柱 I |  | 该折衷的圆柱地图投影由 Waldo Tobler 于 1997 年开发并发布,作为米勒圆柱投影的第一种简化替代方案。 |
| 托布勒圆柱 II |  | 该折衷的圆柱地图投影由 Waldo Tobler 于 1997 年开发并发布,作为米勒圆柱投影的第二种简化替代方案。 |
| 横轴圆柱等积 |  | 该投影为横轴圆柱等积投影。该投影适用于主要南北分布的地图。 |
| 横轴墨卡托 |  | 该投影与墨卡托投影类似,不同之处在于圆柱沿经线而不是赤道与地球相切。生成的投影为等角投影,不会保持真实的方向,适用于绘制大比例或较小区域地图。 |
| 两点等距 |  | 该改进的方位投影用于显示从两个焦点之一到地图上的任何其他点的真实距离。 |
| 范德格林氏 I |  | 该折衷的多圆锥投影用于以圆显示世界。 |
| 垂直近侧透视 |  | 与正射投影不同,此透视投影从有限距离处观察地球。此透视投影效果大致如同从卫星进行观察。 |
| 瓦格纳 IV |  | 该伪圆柱等积投影主要用于专题世界地图。 |
| 瓦格纳 V | 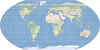 | 该折衷的伪圆柱投影主要用于世界地图。 |
| 瓦格纳 VII | 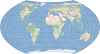 | 该等积投影是兰勃特方位等积投影的改进投影。它也被称为哈默-瓦格纳投影,主要用于世界专题地图。 |
| 温克尔 I |  | 该伪圆柱投影用于对等距圆柱投影和正弦曲线投影的坐标求平均值。 |
| 温克尔 II |  | 该伪圆柱投影用于对等距圆柱投影和摩尔维特投影的坐标求平均值。 |
| 温克尔三重 |  | 该折衷投影适用于世界地图,用于对等距圆柱投影和埃托夫投影的坐标求平均值。国家地理学会使用该投影绘制通用世界地图。 |
地图投影——1 投影目录
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.hqwc.cn/news/99076.html
如若内容造成侵权/违法违规/事实不符,请联系编程知识网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
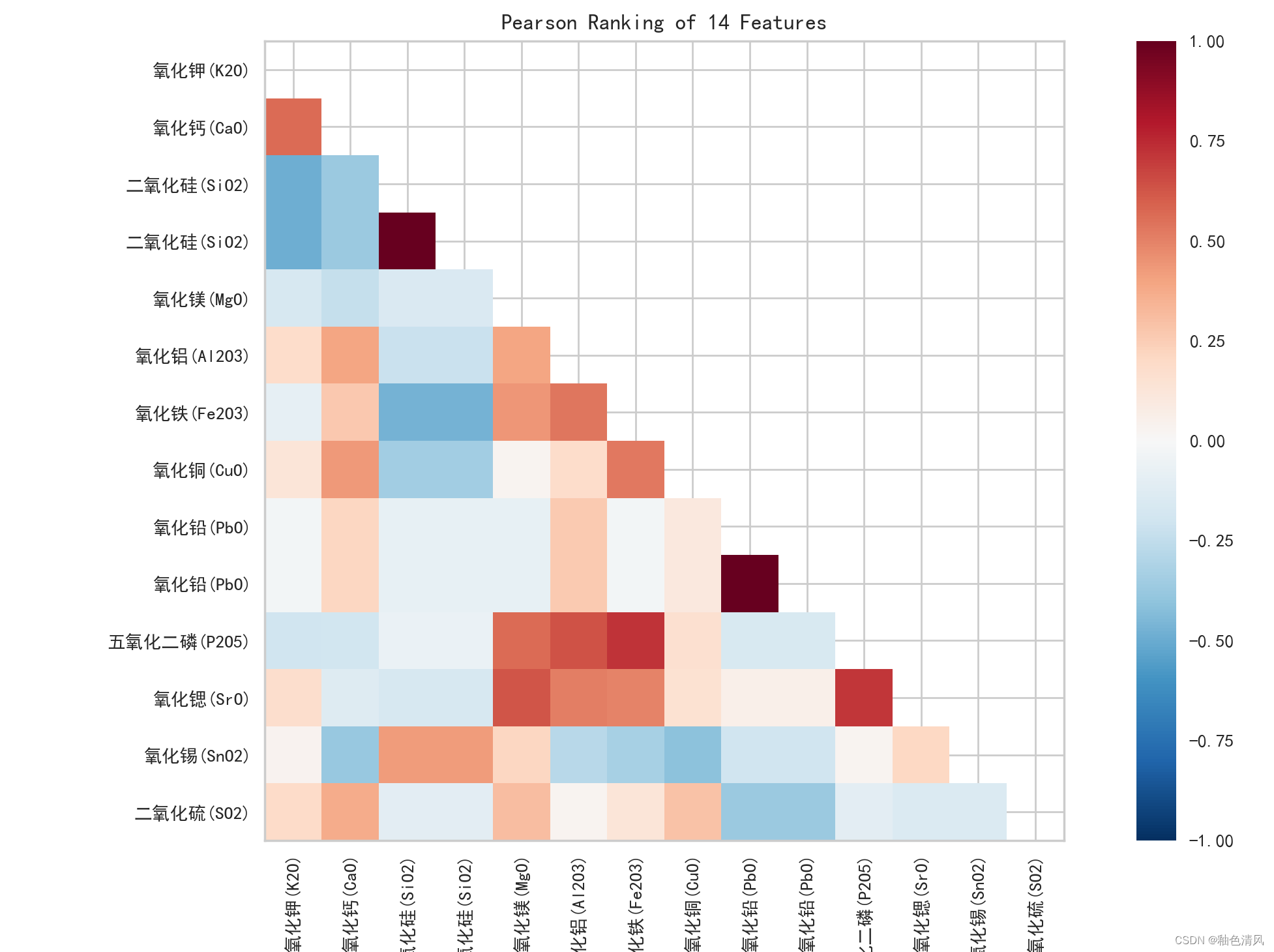
【Yellowbrick】特征可视化分析
Yellowbrick特征可视化分析 ⭐Yellowbrick⭐特征分析可视化⭐Rank1D⭐Rank2D ⭐Yellowbrick
Yellowbrick是一个用于可视化机器学习模型和评估性能的Python库。它提供了一系列高级可视化工具,帮助数据科学家和机器学习从业者更好地理解、调试和优化他们的模型。 它在…
JVM性能优化 —— 类加载器,手动实现类的热加载
一、类加载的机制的层次结构
每个编写的”.java”拓展名类文件都存储着需要执行的程序逻辑,这些”.java”文件经过Java编译器编译成拓展名为”.class”的文件,”.class”文件中保存着Java代码经转换后的虚拟机指令,当需要使用某个类时&#…
react利用wangEditor写评论和@功能
先引入wangeditor写评论功能
import React, { useEffect, useState, useRef, forwardRef, useImperativeHandle } from react;
import wangeditor/editor/dist/css/style.css;
import { Editor, Toolbar } from wangeditor/editor-for-react;
import { Button, Card, Col, For…
文件包含漏洞利用的几种方法
文章目录 安装环境启动环境漏洞花式利用蚁剑连接图片马读取敏感文件(hosts)读取该网站的php源码 代码审计 安装环境
安装phpstudy,下载MetInfo 5.0.4版本软件,复制到phpstudy目录下的www目录中。
打开phpstudy,访问浏…
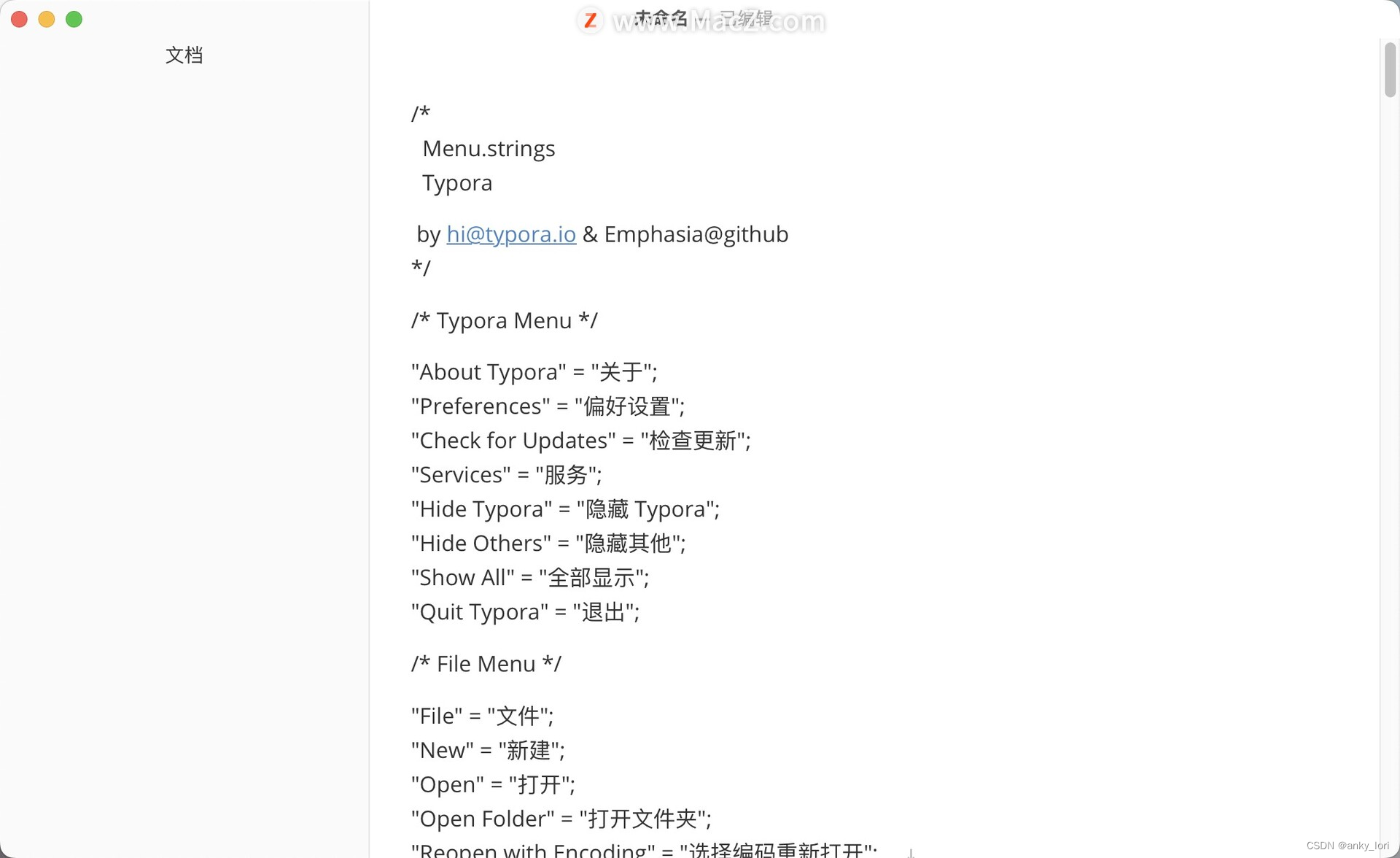
Typora for Mac(Markdown文本编辑器)
Typora是一款简洁、直观的跨平台Markdown编辑器软件。它提供了一个非常直观和简单的界面,让用户可以更轻松地编写和编辑Markdown语言的文档。 Typora具有实时预览功能,这意味着你可以在编辑Markdown文档的同时立即看到最终的效果。它允许用户快速切换编辑…
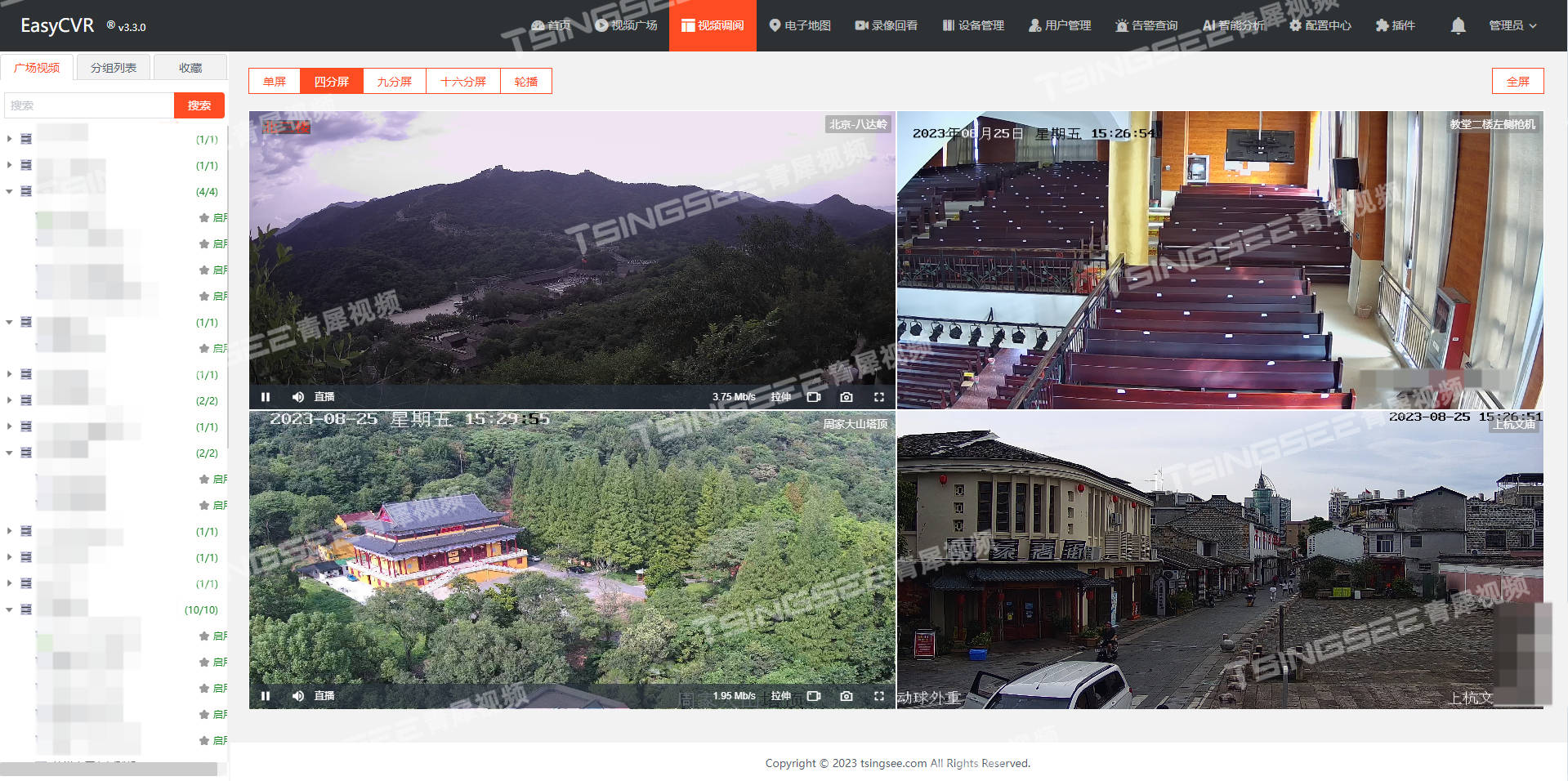
视频监控/视频云存储EasyCVR平台接入华为ivs3800平台提示400报错,如何解决?
开源EasyDarwin视频监控TSINGSEE青犀视频平台EasyCVR能在复杂的网络环境中,将分散的各类视频资源进行统一汇聚、整合、集中管理,在视频监控播放上,视频云存储/安防监控汇聚平台可支持1、4、9、16个画面窗口播放,可同时播放多路视频…
【个人博客系统网站】项目的发布 · 通过公网IP访问我们的网站 · 思考总结
【JavaEE】进阶 个人博客系统(6) 文章目录 【JavaEE】进阶 个人博客系统(6)1. 项目发布1.1 后端代码修改1.1.1 数据库密码1.1.2 端口号修改1.1.3 文件保存地址修改1.1.4 静态资源映射修改 1.2 云服务器1.2.1 建库建表1.2.2 必要…
通过rabbitmq生成延时消息,并生成rabbitmq镜像
通过rabbitmq生成延时消息队列,并生成rabbitmq镜像 整体描述1. 使用场景2. 目前问题3. 前期准备 具体步骤1. 拉取镜像2. 运行镜像3. 安装插件4. 代码支持4.1 config文件4.2 消费监听4.2 消息生产 5. 功能测试 镜像操作1. 镜像制作2. 镜像导入 总结 整体描述
1. 使用…
vue集成mars3d后,basemaps加不上去
首先:
<template> <div id"centerDiv" class"mapcontainer"> <mars-map :url"configUrl" οnlοad"onMapload" /> </div>
</template> <script>
import MarsMap from ../component…
Vue + Element UI 前端篇(三):工具模块封装
Vue Element UI 实现权限管理系统 前端篇(三):工具模块封装
封装 axios 模块
封装背景
使用axios发起一个请求是比较简单的事情,但是axios没有进行封装复用,项目越来越大,会引起越来越多的代码冗余&am…
Kotlin(五) 循环语句
目录
For循环
关键字
until
step
downTo Java中主要有两种循环语句:while循环和for循环。而Kotlin也提供了while循环和for循环,其中while循环不管是在语法还是使用技巧上都和Java中的while循环没有任何区别,因此我们就直接跳过不进行讲解…
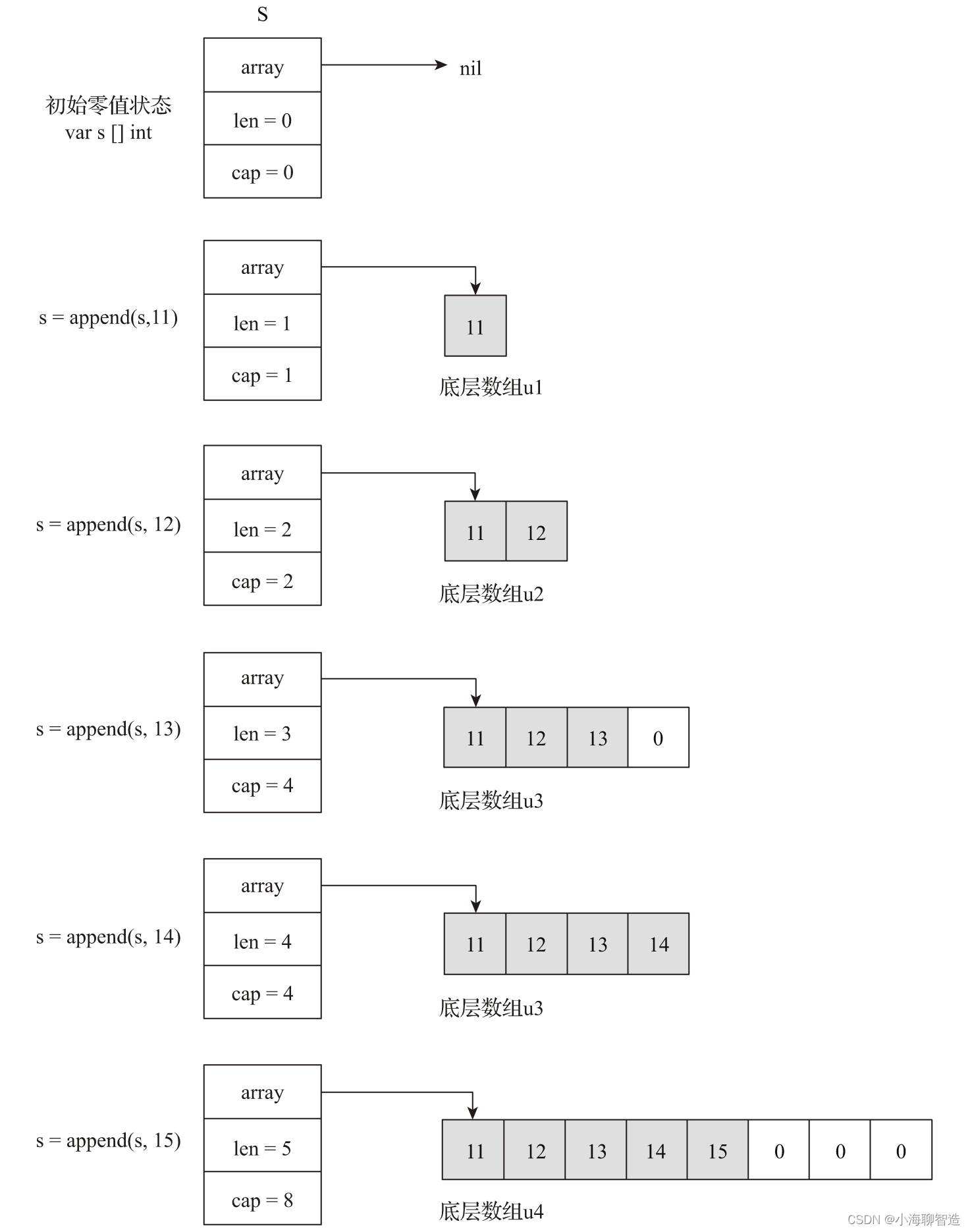
小白学go基础06-了解切片实现原理并高效使用
slice,中文多译为切片,是Go语言在数组之上提供的一个重要的抽象数据类型。在Go语言中,对于绝大多数需要使用数组的场合,切片实现了完美替代。并且和数组相比,切片提供了更灵活、更高效的数据序列访问接口。 切片究竟是…