凸壳取点
现在平面上有 n n n个点: ( x i , y i ) (x_i,y_i) (xi,yi)
现有一次函数: y = k x + b y=kx+b y=kx+b。
要求一次函数必须至少经过平面当中的一个点。则一次函数可以写作: y i = k ⋅ x i + b y_i=k\cdot x_i+b yi=k⋅xi+b
如果斜率 k k k固定,则这样的一次函数会有 n n n条。
现在要求截距 b b b最小的那个一次函数。
那么这个问题相当于拿着一条斜率为 k k k的直线从下往上扫,碰到的第一个点对应的一次函数即为答案。
如果斜率 k k k不固定呢?
那么只有这些点形成的下凸壳上的点有可能被碰到(和 k k k的正负性没关系):
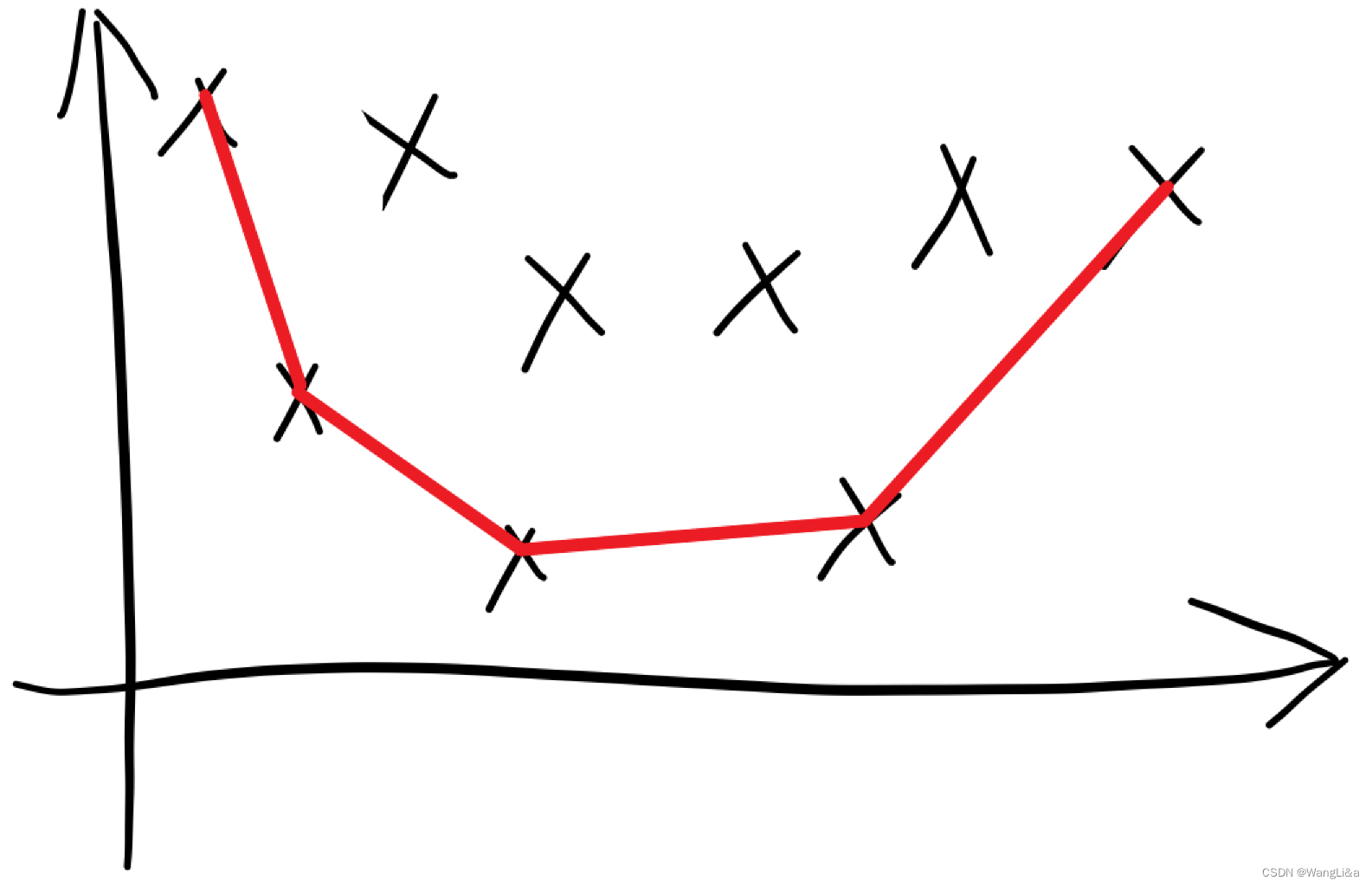
下凸壳上的直线斜率是单调递增的。数据结构维护下凸壳就可以快速查到答案。
那如果要最大化截距呢?
数据结构维护上凸壳就可以了,上凸壳上的直线斜率单调递减。
简单斜率优化
模板题
首先求出 c i c_i ci的前缀和 s i s_i si。设 f i f_i fi表示前 i i i个单词,在第 i i i个单词处换行的最小价值。
转移考虑上一次在哪里换行: f i = min j = 0 i − 1 { f j + ( s i − s j ) 2 + M } f_i=\overset{i-1}{\underset{j=0}\min}\{f_j+(s_i-s_j)^2+M\} fi=j=0mini−1{fj+(si−sj)2+M}
处理一下: f i = min j = 0 i − 1 { f j + s j 2 − 2 s i s j } + s i 2 + M f_i=\overset{i-1}{\underset{j=0}\min}\{f_j+s_j^2-2s_is_j\}+s_i^2+M fi=j=0mini−1{fj+sj2−2sisj}+si2+M
到这一步还是看不出啥。
我们可以假设 j j j是 i i i转移的前驱,这样的话就可以去掉 min \min min:
f i = f j + s j 2 − 2 s i s j + s i 2 + M f_i=f_j+s_j^2-2s_is_j+s_i^2+M fi=fj+sj2−2sisj+si2+M
因为我们现在是对 f i f_i fi作转移,所以可以把只与 i i i有关的部分看做常数,然后把式子分成三个部分:
- 只与 i i i有关的部分,或者常数( b b b)
- 只与 j j j有关的部分( y y y)
- 与 i , j i,j i,j都有关的部分( k ⋅ x k\cdot x k⋅x)
写出来就是:
f j + s j 2 = 2 s i s j + f i − s i 2 − M f_j+s_j^2=2s_is_j+f_i-s_i^2-M fj+sj2=2sisj+fi−si2−M
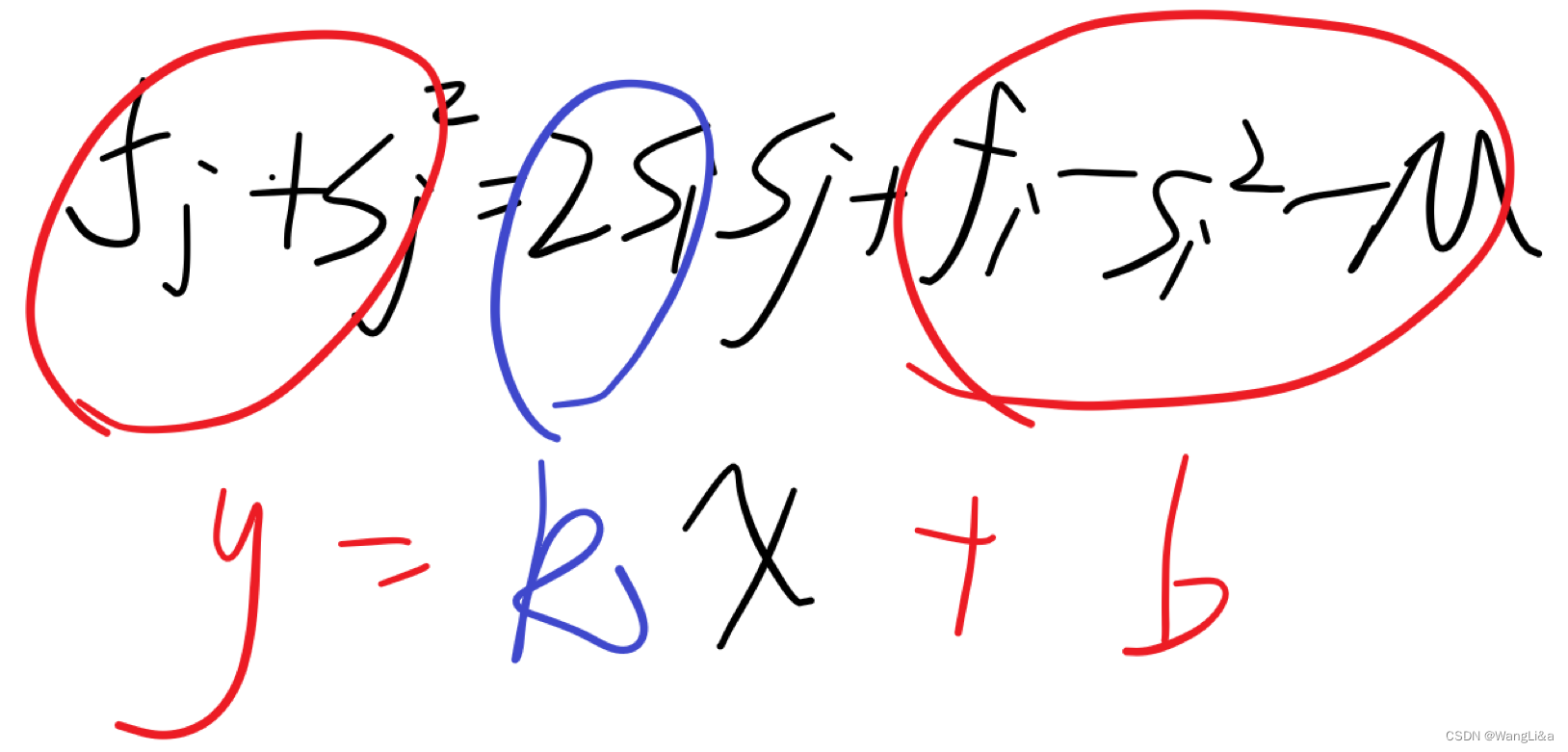
因为我们是假设 j j j是 i i i的前驱,而事实上还不知道哪个 j j j是 i i i的前驱,所以这样的 j j j一共有 i i i个,分别为 j = 0 , j = 1 , . . . , j = i − 1 j=0,j=1,...,j=i-1 j=0,j=1,...,j=i−1:
映射成点就是 ( s j , f j + s j 2 ) \left(s_j,f_j+s_j^2\right) (sj,fj+sj2),而我们要最小化 f i f_i fi,就是要最小化截距 b b b,这就是一个下凸壳取点问题。
接下来说一下如何用数据结构去维护凸壳:
当我们更新完了目前的 f i f_i fi之后, f i f_i fi就应该被加入到凸壳里,下凸壳的斜率单调递增,我们用单调队列维护相邻两点之间的斜率单调递增:
- 之前在凸壳里的点编号都在 [ 0 , i − 1 ] [0,i-1] [0,i−1]之间
- 由于 s s s单调递增,因此点 i i i一定处于凸壳的最右侧的右边
while:如果队列末尾两点的斜率,和队尾与新点的斜率不符合单调递增,那么队尾出队- 节点 i i i从队尾入队(节点 i i i无论如何都会加入凸壳,因为就算没有队尾被弹出,也是不加白不加)
接下来说一下如何取出答案:
首先可以考虑到凸壳上的直线斜率单调递增,我们的最优决策点应该满足:它左侧连接的直线斜率比 k k k小,右边的斜率比 k k k大。
因此最优决策点是:第一个满足斜率大于 k k k的直线的左端点,因此可以直接在单调队列上二分。
接下来考虑到,由于 k = 2 s i k=2s_i k=2si,我们枚举 i i i,而 s s s单调递增,因此如果凸壳上的一条线现在斜率已经 < k <k <k,则它的左端点都不可能是答案了,因此可以直接弹出队头。
具体说一下是这样的:
while:我们检查单调队列的队头,如果队头前两点的斜率 < k <k <k,则弹出队头- 取出此时的队头,设为 j j j
- f i = f j + ( s i − s j ) 2 + M f_i=f_j+(s_i-s_j)^2+M fi=fj+(si−sj)2+M
最后一提,我们计算两点间斜率用:
k = Δ y Δ x = y 2 − y 1 x 2 − x 1 k=\frac{\Delta y}{\Delta x}=\frac{y_2-y_1}{x_2-x_1} k=ΔxΔy=x2−x1y2−y1
完整代码是这样的:
#include<iostream>
using namespace std;
const int N=5e5;
long long s[N+5];
long long f[N+5];
int q[N+5];
double sl(int x,int y) {计算两点之间的斜率return s[x]^s[y]?(double(f[x])+s[x]*s[x]-f[y]-s[y]*s[y])/(s[x]-s[y]):1e18;如果dx=0返回极大值,此时斜率为正无穷。
}
int main() {int n;long long m;while(cin>>n>>m) {for(int i=1;i<=n;i++) (cin>>s[i]),s[i]+=s[i-1];前缀和int h=1,t=0;h队头,t队尾,左闭右闭 for(int i=1;i<=n;i++) {接下来两行是更新队尾,我们在i时将i-1对应的节点加入队尾:h<t保证队中至少有两个节点while(h<t&&sl(i-1,q[t])<=sl(q[t-1],q[t])) t--;如果加入i-1会导致不满足下凸壳斜率单调递增,就弹出队尾q[++t]=i-1;加入i-1接下来两行更新队头,找到最优决策点:while(h<t&&sl(q[h],q[h+1])<=(double)2*s[i]) h++;如果队头两点斜率<k,弹出队头int j=q[h];点j即为最优决策点f[i]=f[j]+(s[i]-s[j])*(s[i]-s[j])+m;}cout<<f[n]<<endl;}
}
模板题2
会了斜率优化模板的话主要是个结论题。
首先考虑到把土地的长和宽放到坐标轴上(这一步和斜率优化没关系):
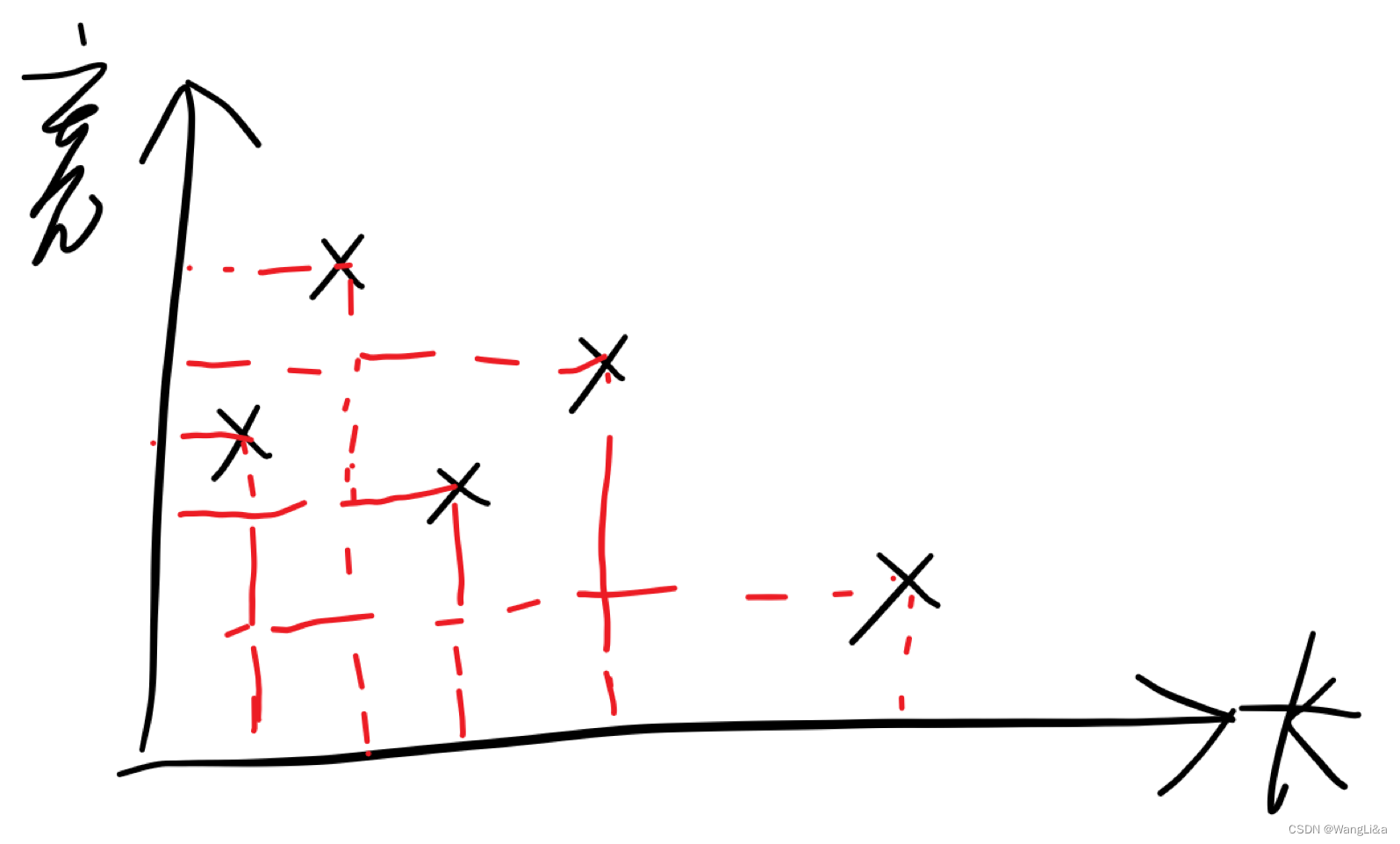
我们会发现如果一个点与坐标轴围成的矩形如果完全被另外的矩形覆盖了,那么这个点对答案的贡献就是0,可以删掉了。
删去之后图就是这个样子的:
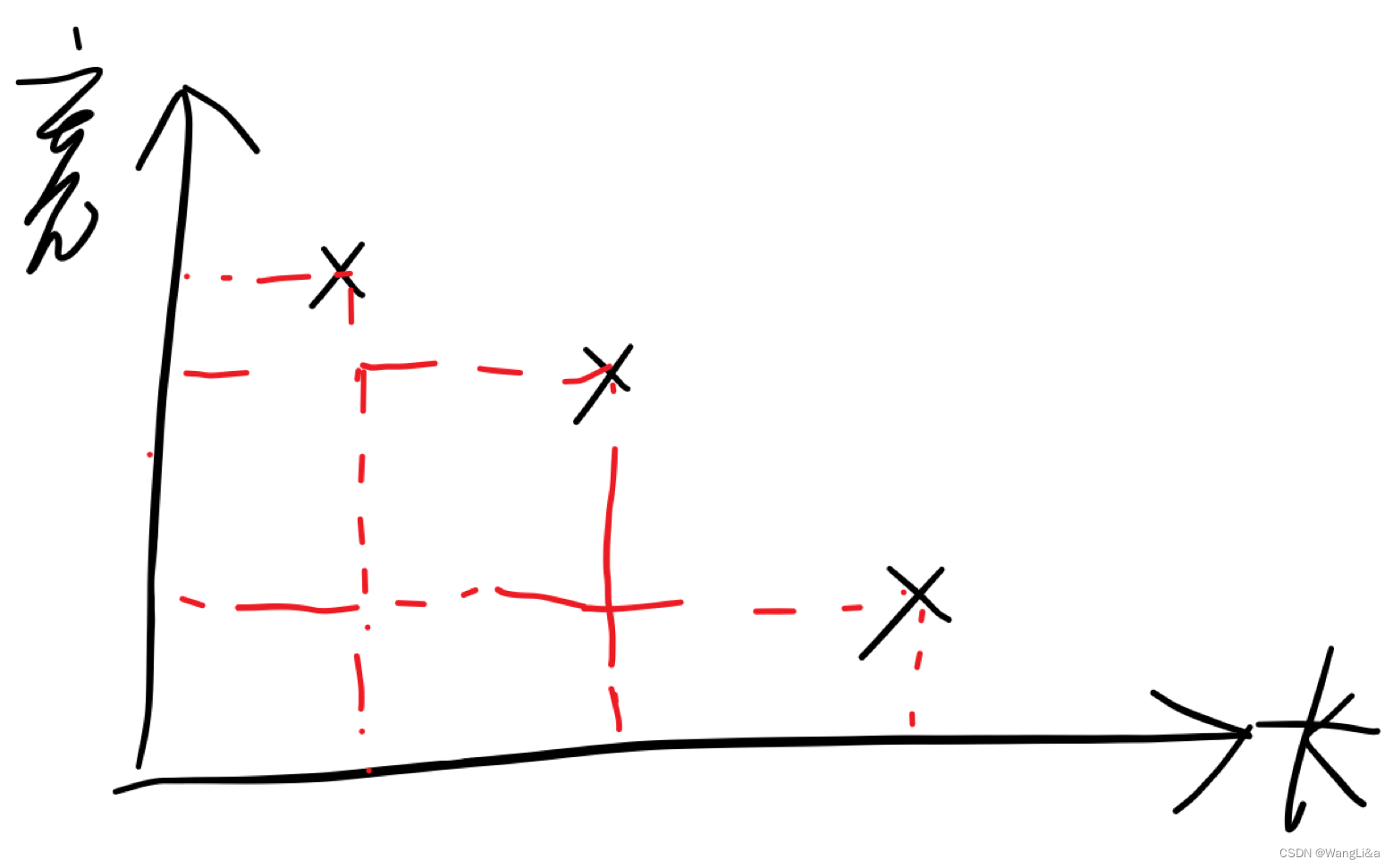
于是我们可以按照横坐标给他们编号:
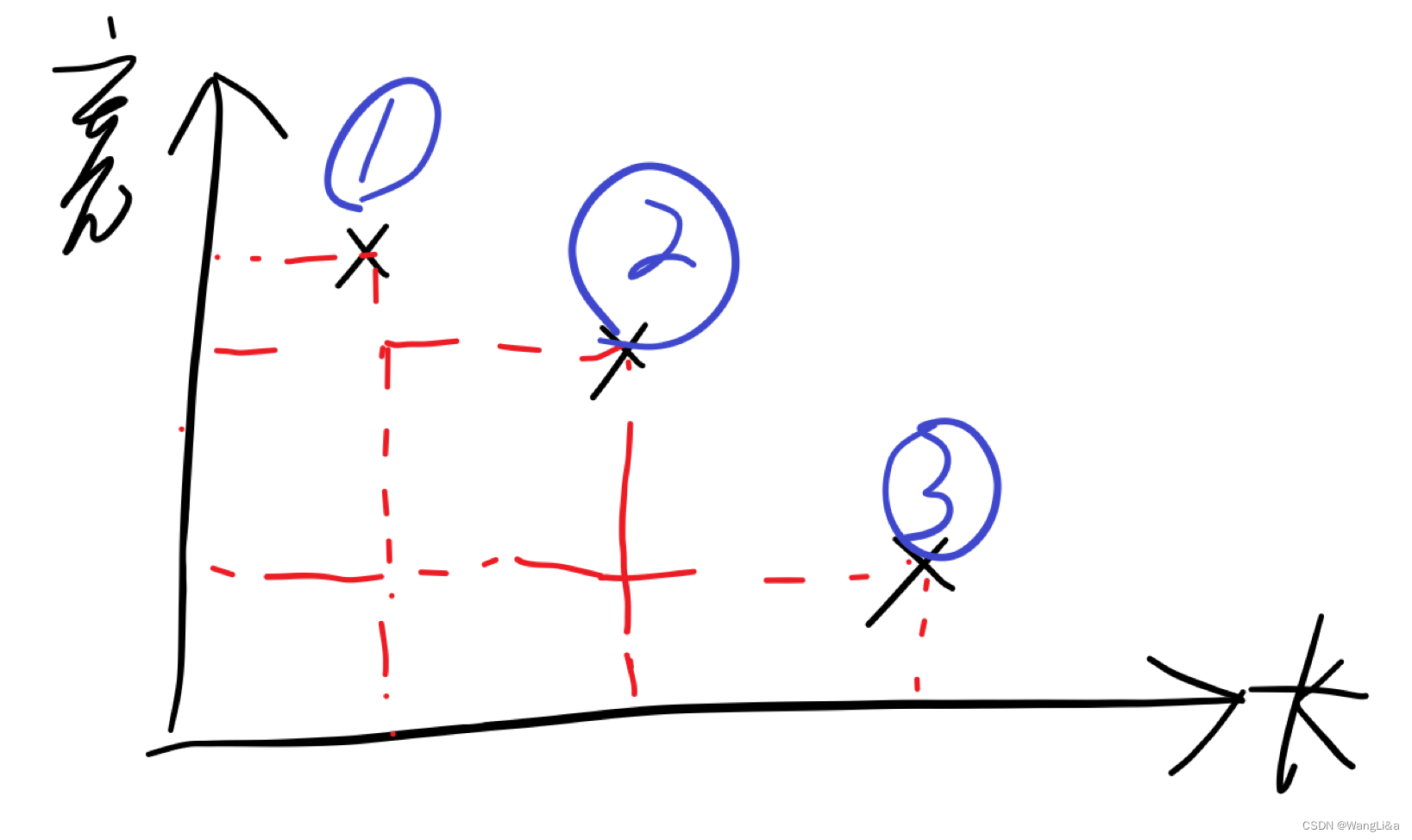
然后我们会发现,如果把1、3合并起来,会得到一个大矩形:
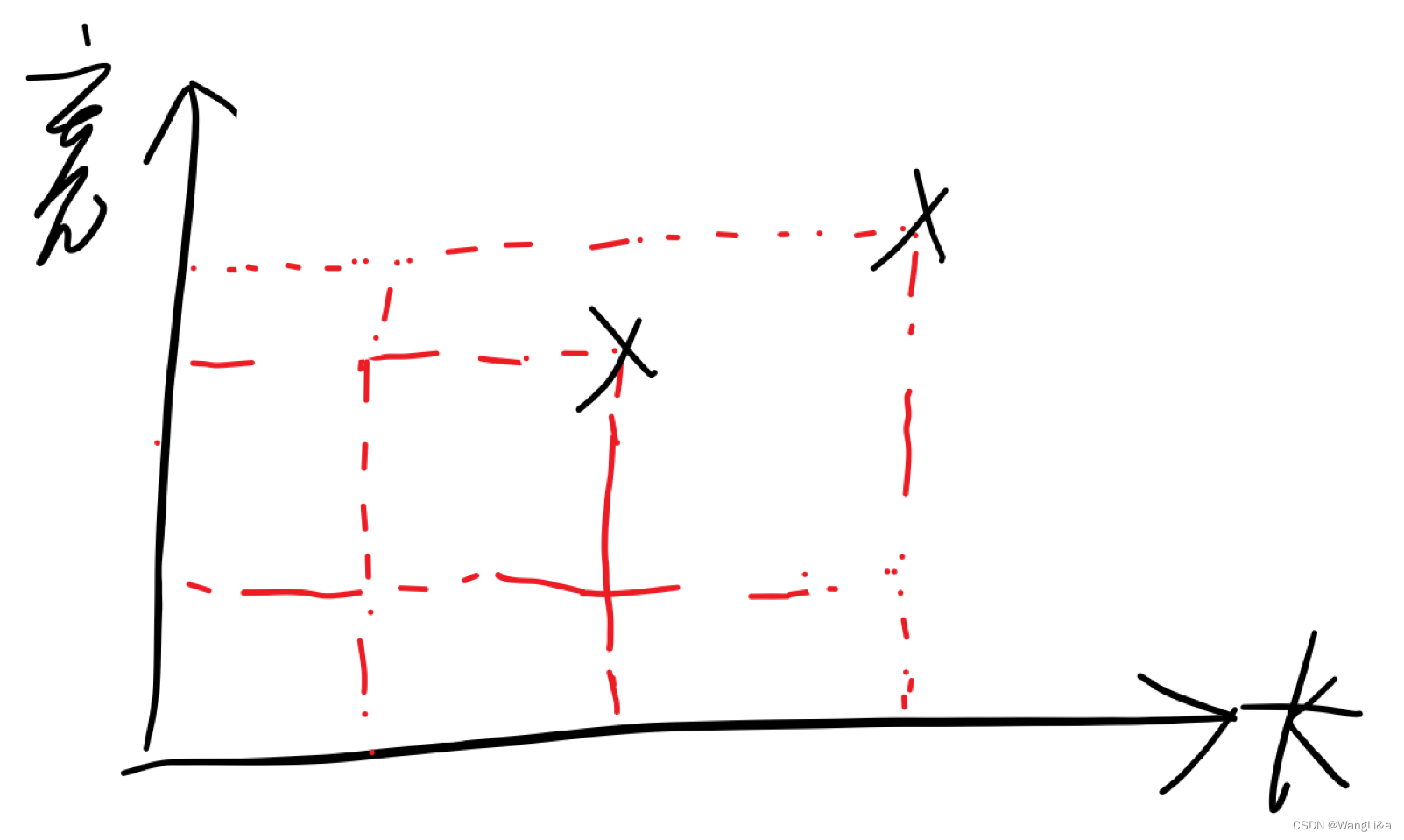
此时把2并购进去肯定更优。
因此我们就知道,去除包含关系的矩形之后,把剩下的矩形按照一维排列并编号,那么一定有一种最优情况下的并购方案,都是把一些编号连续段并购起来。
因此可以dp(已去除包含的矩形,并按长度排序,并且重新编号):
设 f i f_i fi表示前 i i i个矩形的最小贡献。
转移考虑这一次并购编号 [ j + 1 , i ] [j+1,i] [j+1,i]连续段:
f i = min j = 0 i − 1 { f j + x i ⋅ y j + 1 } f_i=\overset{i-1}{\underset{j=0}\min}\{f_j+x_i\cdot y_{j+1}\} fi=j=0mini−1{fj+xi⋅yj+1}
去掉 min \min min以后是这样的:
f j = − x i ⋅ y j + 1 + f i f_j=-x_i\cdot y_{j+1}+f_i fj=−xi⋅yj+1+fi
单调队列维护下凸壳,斜率优化。
代码:
#include<algorithm>
#include<map>
#include<iostream>
using namespace std;
const int N=5e4;
pair<long long,long long> a[N+5];
pair<long long,long long> b[N+5];
long long f[N+5];
long long nxt[N+5];
int q[N+5],h=1,t;
double sl(int x,int y) {return (double(f[x])-f[y])/(b[x+1].second-b[y+1].second);dx不可能等于0,因为去掉了包含关系的节点
}
int main() {int n;cin>>n;for(int i=1;i<=n;i++) cin>>a[i].first>>a[i].second;sort(a+1,a+1+n);
// cout<<"***"<<endl;
// for(int i=1;i<=n;i++) cout<<a[i].first<<' '<<a[i].second<<endl;for(int i=n;i;i--) nxt[i]=max(nxt[i+1],a[i+1].second);去掉具有包含关系的矩形的方法是,按照一维排序,然后求一下第二维的后缀max如果两维全部存在一个比自身大矩形的,那么就去掉当然也可以打二维偏序
// cout<<"***"<<endl;
// for(int i=1;i<=n;i++) cout<<nxt[i]<<' ';
// cout<<endl;int m=0;for(int i=1;i<=n;i++)if(a[i].second>nxt[i]) b[++m]=a[i];————————重新编号
// cout<<"***"<<endl;
// for(int i=1;i<=m;i++) cout<<b[i].first<<' '<<b[i].second<<endl;for(int i=1;i<=m;i++) {while(h<t&&sl(q[t],i-1)>=sl(q[t-1],q[t])) t--;q[++t]=i-1;while(h<t&&sl(q[h],q[h+1])>=-b[i].first) h++;int j=q[h];f[i]=f[j]+b[i].first*b[j+1].second; }cout<<f[m];
}
模板题3
超级推荐的题解视频
首先考虑安排任务会对后面的所有的操作产生贡献,因此有后效性,不能直接dp。
考虑去后效性。
考虑把后效性记进状态里:
设 f i , j f_{i,j} fi,j表示分了 i i i批,目前考虑完了前 j j j个任务的最小贡献。复杂度过高,不再考虑。
考虑由于贡献可以拆开,因此可以费用提前计算,这样就不再有后效性。
设 f i f_i fi表示考虑了前 i i i个任务,并且 i i i作为一批任务结尾的费用,加上这些任务对后面任务产生的额外的费用,的最小值。
用 a a a表示时间的前缀和,用 b b b表示费用的前缀和,记 m = s m=s m=s。
转移就是枚举上一批任务在哪里: f i = min j = 0 i − 1 { f j + m ( b n − b j ) + a i ( b i − b j ) } f_i=\overset{i-1}{\underset{j=0}{\min}}\left\{f_j+m(b_n-b_j)+a_i(b_i-b_j)\right\} fi=j=0mini−1{fj+m(bn−bj)+ai(bi−bj)}
其中 m ( b n − b j ) m(b_n-b_j) m(bn−bj)表示的是当前批次任务对接下来的任务产生的影响导致其产生的贡献, a i ( b i − b j ) a_i(b_i-b_j) ai(bi−bj)表示当前任务对答案的贡献。
很明显可以斜率优化,单调队列维护下凸壳就可以。
#include<algorithm>
#include<map>
#include<iostream>
using namespace std;
const int N=3e5;
long long a[N+5],b[N+5];
int q[N+5],h=1,t;
long long f[N+5];
int n;
long long m;
double sl(int x,int y) {return b[x]^b[y]?((double)f[x]-m*b[x]-f[y]+m*b[y])/(b[x]-b[y]):1e-18;
}
int main() {cin>>n>>m;for(int i=1;i<=n;i++) (cin>>a[i]>>b[i]),a[i]+=a[i-1],b[i]+=b[i-1];for(int i=1;i<=n;i++) {while(h<t&&sl(q[t-1],q[t])>=sl(q[t],i-1)) t--;q[++t]=i-1;while(h<t&&sl(q[h],q[h+1])<=a[i]) h++;int j=q[h];f[i]=f[j]+m*(b[n]-b[j])+a[i]*(b[i]-b[j]);}cout<<f[n];
}
dx与dy表示斜率
题目本身没啥好说的,单调队列维护斜率优化板子。
但是我们知道double运算会有精度问题,计算斜率可能会被卡。
因此我们知道: k = Δ y Δ x k=\frac{\Delta y}{\Delta x} k=ΔxΔy
所以说比较 k < K k<K k<K相当于:
y 2 − y 1 x 2 − x 1 < Y 2 − Y 1 X 2 − X 1 \frac{y_2-y_1}{x_2-x_1}<\frac{Y_2-Y_1}{X_2-X_1} x2−x1y2−y1<X2−X1Y2−Y1
即: ( y 2 − y 1 ) ( X 2 − X 1 ) < ( Y 2 − Y 1 ) ( x 2 − x 1 ) {(y_2-y_1)}{(X_2-X_1)}<{(Y_2-Y_1)}{(x_2-x_1)} (y2−y1)(X2−X1)<(Y2−Y1)(x2−x1)
这样可以long long比较,不会有精度问题。
注意dx不能为负数,否则可能会出现变号的问题。
而且这样在dx=0时也是对的,我们就拿下凸壳来举例:
如果现在要加入一个 i − 1 i-1 i−1,且 Δ x i − 1 , q [ t ] = 0 \Delta x_{i-1,q[t]}=0 Δxi−1,q[t]=0,则此时:
-
如果 d y ≥ 0 dy\geq 0 dy≥0,则不需要弹出队尾,直接加入,恰好不需要特判:
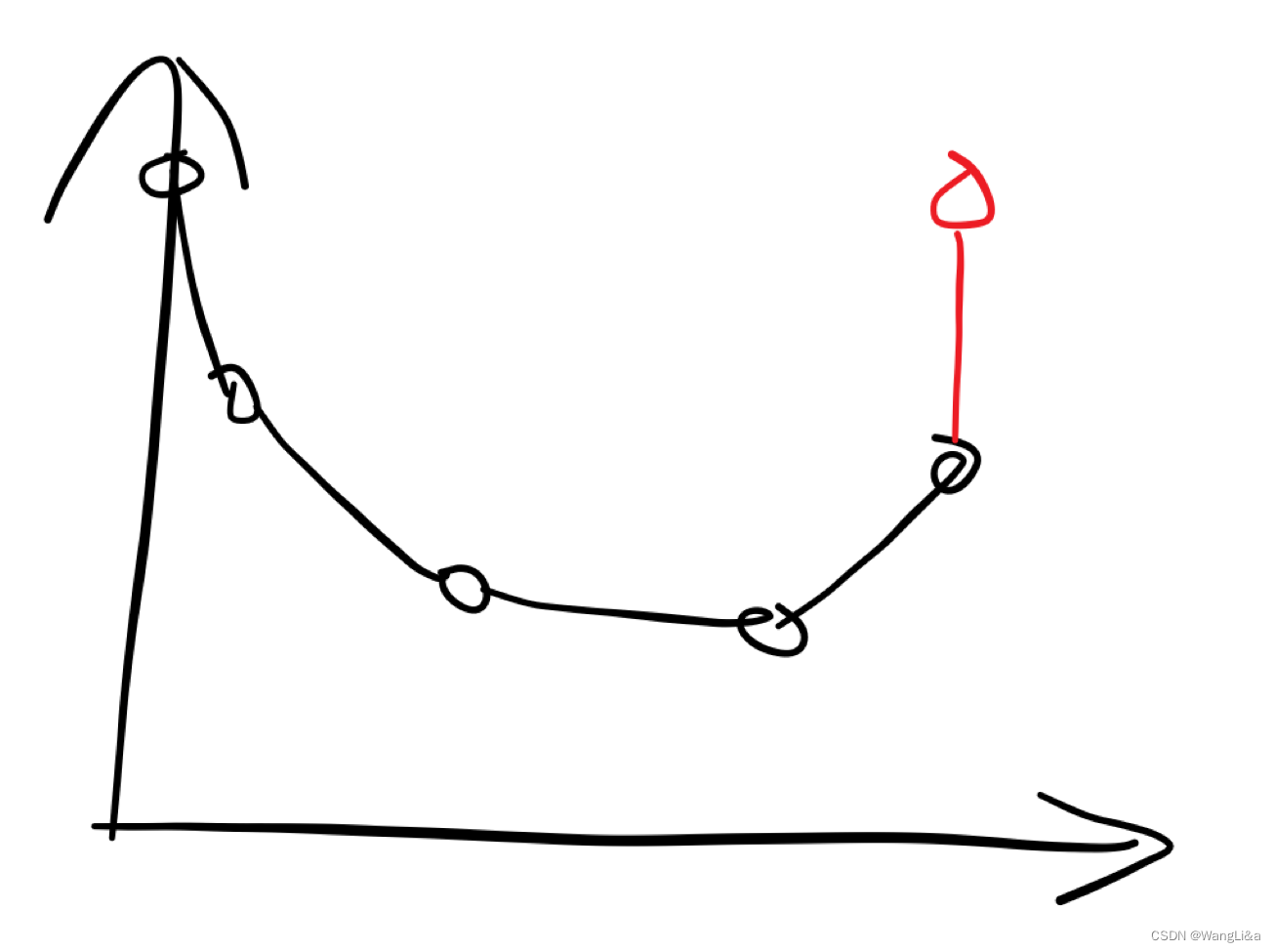
-
如果 d y ≤ 0 dy\leq 0 dy≤0,则需要弹出队尾,恰好不需要特判:
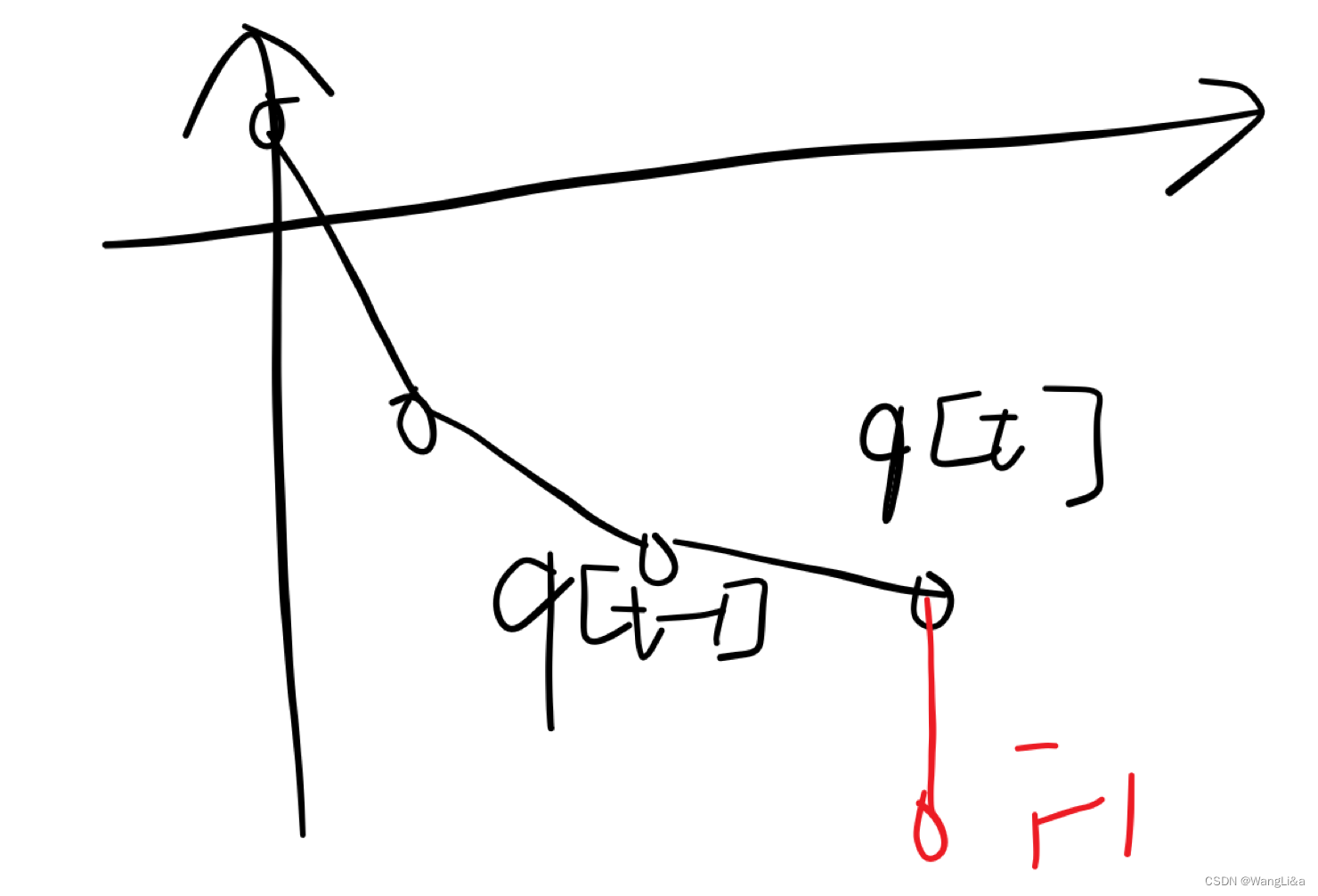
在维护上凸壳,或者弹出队头的时候,我们会发现把除法化为乘积仍然恰好符合情况,均不需要特判。
因此以后我们就都写成乘积的形式好了。
代码如下:
#include<iostream>
#include<algorithm>
#include<cstdio>
using namespace std;
const int N=1e6;
int n;
long long a,b,c;
long long s[N+5],f[N+5];
int q[N+5],h=1,t;
long long dx(int x,int y) {return s[x]-s[y];
}
long long dy(int x,int y) {return f[x]+a*s[x]*s[x]-b*s[x]-(f[y]+a*s[y]*s[y]-b*s[y]);
}
int main() {cin>>n>>a>>b>>c;for(int i=1;i<=n;i++) (cin>>s[i]),s[i]+=s[i-1];for(int i=1;i<=n;i++) {while(h<t&&dy(i-1,q[t])*dx(q[t],q[t-1])>=dy(q[t],q[t-1])*dx(i-1,q[t])) t--;q[++t]=i-1;while(h<t&&dy(q[h+1],q[h])>=2*a*s[i]*dx(q[h+1],q[h])) h++;int j=q[h];f[i]=f[j]+a*(s[i]-s[j])*(s[i]-s[j])+b*(s[i]-s[j])+c;}cout<<f[n];
}
权值下放
题解视频
注意到容器的长度含有的项有点多,可能比较难处理,我们可以考虑把 j − i j-i j−i下放到每一个物品中,考虑 a i = c i + 1 a_i=c_i+1 ai=ci+1,用 s s s表示 a a a的前缀和,则 x = s i − s j − 1 x=s_i-s_j-1 x=si−sj−1。
这样就变成了板子。
#include<iostream>
using namespace std;
const int N=5e4;
istream& operator>>(istream& is,__int128&x) {long long t;is>>t;x=t;return is;
}
__int128 s[N+5],f[N+5];
int n;
__int128 K;
__int128 dx(int x,int y) {return s[x]-s[y];
}
__int128 dy(int x,int y) {return f[x]+s[x]*s[x]+2*s[x]*K-(f[y]+s[y]*s[y]+2*s[y]*K);
}
int q[N+5],h=1,t;
int main() {cin>>n>>K;K++;for(int i=1;i<=n;i++) (cin>>s[i]),s[i]+=s[i-1]+1; 我们把i-j这些权值分配到每一个元素上for(int i=1;i<=n;i++) {while(h<t&&dy(q[t],q[t-1])*dx(i-1,q[t])>=dy(i-1,q[t])*dx(q[t],q[t-1])) t--;q[++t]=i-1;while(h<t&&dy(q[h+1],q[h])<=2*s[i]*dx(q[h+1],q[h])) h++;int j=q[h];f[i]=f[j]+(s[i]-s[j]-K)*(s[i]-s[j]-K);}cout<<(long long)f[n];}
性质题
我竟然想了半个小时。
盲猜一波最后贡献只与划分的位置有关,与划分顺序无关。
证明可以考虑这两种方法:
- 假设序列中有两个元素,设为 x , y x,y x,y,假设 x , y x,y x,y之间没有被分割任何一次,则 x y xy xy在答案中不做贡献,否则无论中间被分割了多少次,也无论顺序如何,只做一次贡献。证毕。
- 一开始我想到的证法:
我们考虑到,假设在最优答案中,一个子段如果没有被分开,那么就可以把它替换成一个新的元素,这个元素的大小是它的子段和。
接下来考虑到:
情况一:如果一个子段 X X X和另一个子段 Y Y Y在之前就已经分开,接下来会对 X X X操作一步,再会对 Y Y Y操作一步,那么显然这两步之间互不影响,先对谁操作无关紧要。
情况二:现在我们假设段 U U U是一个没有被分开的极大连通块,然后 U U U我们用两步分将 U U U成了 X ∣ Y ∣ Z X|Y|Z X∣Y∣Z三块:
这样的话会有两种分法:
①:第一步: X ∣ Y , Z X|Y,Z X∣Y,Z,第二步: X ∣ Y ∣ Z X|Y|Z X∣Y∣Z,贡献是 X ( Y + Z ) + Y Z = X Y + X Z + Y Z X(Y+Z)+YZ=XY+XZ+YZ X(Y+Z)+YZ=XY+XZ+YZ
②:第一步: X , Y ∣ Z X,Y|Z X,Y∣Z,第二步: X ∣ Y ∣ Z X|Y|Z X∣Y∣Z,贡献是 ( X + Y ) Z + X Y = X Y + X Z + Y Z (X+Y)Z+XY=XY+XZ+YZ (X+Y)Z+XY=XY+XZ+YZ
贡献相同。
因此我们就知道,如果把答案写成一个操作序列,序列的第 i i i个元素表示第 i i i步在哪个位置划分一刀,则无论相邻的两步操作的位置原来属于一个连续段(情况二),还是早已被分开(情况一),则我们都可以交换操作序列相邻的两项,且保证答案不变。这证明操作序列的所有排列对应的答案是相同的。
然后就是斜率优化板子。
#include<iostream>
#include<algorithm>
#include<cstdio>
using namespace std;
const int N=1e5;
int n,K;
long long s[N+5];
long long f[205][N+5];
int q[N+5];
long long dx(int x,int y,int k) {return s[x]-s[y];
}
long long dy(int x,int y,int k) {return f[k][x]-s[x]*s[x]-(f[k][y]-s[y]*s[y]);
}
int nxt[205][N+5];
void dfs(int k,int i) {if(!k) return ;dfs(k-1,nxt[k][i]);cout<<nxt[k][i]<<' ';
}
int main() {cin>>n>>K;for(int i=1;i<=n;i++) (cin>>s[i]),s[i]+=s[i-1];for(int k=1;k<=K;k++) {int h=1,t=0;for(int i=2;i<=n;i++) {while(h<t&&dy(i-1,q[t],k-1)*dx(q[t],q[t-1],k-1)>=dy(q[t],q[t-1],k-1)*dx(i-1,q[t],k-1)) t--;q[++t]=i-1;while(h<t&&dy(q[h+1],q[h],k-1)>=-s[i]*dx(q[h+1],q[h],k-1)) h++;int j=q[h];nxt[k][i]=j;f[k][i]=f[k-1][j]+s[j]*(s[i]-s[j]);}}
// for(int k=1;k<=K;k++,cout<<endl)
// for(int i=1;i<=n;i++)
// cout<<"f["<<k<<"]["<<i<<"]="<<f[k][i]<<':'<<nxt[k][i]<<' ';cout<<f[K][n]<<endl;dfs(K,n);
}
维护上凸壳。
双层状态单调队列
题解视频
设 a i ( i ≥ 2 ) a_i(i\geq 2) ai(i≥2)表示山头的相对距离。
b i = b i − 1 + a i b_i=b_{i-1}+a_i bi=bi−1+ai,表示山头的绝对距离。
接下来的范围是 m m m:
c i c_i ci表示猫所属山头
d i d_i di表示猫玩到第几秒
则设出发时为 x x x秒,能接到猫当且仅当 x + b c i ≥ d i x+b_{c_i}\geq d_i x+bci≥di,因此设 h i = d i − b c i h_i=d_i-b_{c_i} hi=di−bci, h i h_i hi表示能接到猫的最早出发时间。
这样原问题就和山头以及等待时间没关系了,直接把猫按照 h i h_i hi升序排序,由于能接就接,所以每个人接走的猫一定是排序后的一个连续段对应的猫。
设 g g g表示 h h h的前缀和。
想要直接把时间压进状态里比较难,但是又不能没有时间。不然转移不了。因此我们考虑到把猫按照设成二元组放到坐标系内: ( i , h i ) (i,h_i) (i,hi),假设有一个人从 t t t时刻出发,那么它能接到的猫为 X = { i ∣ h i ≤ t } X=\{i|h_i\leq t\} X={i∣hi≤t},假设他前面一个人接到的猫为 X ′ X' X′,则他实际接到的猫为 X − X ′ X-X' X−X′,对答案产生的贡献为: ∑ x ∈ ( X − X ′ ) t − h x \underset{x\in(X-X')}{\sum}t-h_x x∈(X−X′)∑t−hx,相当于现在坐标系内有一条是水平直线 y = t y=t y=t,则它的贡献是到所有在 X − X ′ X-X' X−X′内的节点的距离之和。显然为了最小化这个距离之和,我们要让 t t t尽可能小,也就是水平直线与点集 X − X ′ X-X' X−X′内纵坐标最高的点相交时,相交即是恰好接到。
这说明最优情况下,每个人最少恰好接到一只猫(除非猫被接完了)
而我们知道一个人一定接走连续段内的一些猫,因此第 i i i个人出发的时间一定恰好是他所接的连续段内的最后一只猫的 h h h值,也就对应着直线(出发时间)与点集最高的点(连续段最后一只猫)相交的情况。
这样就可以设状态了(已排序),设 f i , j f_{i,j} fi,j表示前 i i i个人已接走了前 j j j只猫的最小总时间。
转移就是考虑上一个人接走了哪些猫: f i , j = min k = 0 j − 1 { f i − 1 , k + ( j − k ) h j + g k − g j } f_{i,j}=\overset{j-1}{\underset{k=0}{\min}}\left\{f_{i-1,k}+(j-k)h_j+g_k-g_j\right\} fi,j=k=0minj−1{fi−1,k+(j−k)hj+gk−gj}
斜率优化板子。
唯一需要注意的地方是初值: f 0 , 0 = 0 , f 0 , x ≠ 0 = + ∞ f_{0,0}=0,f_{0,x\neq 0}=+\infty f0,0=0,f0,x=0=+∞
#include<iostream>
#include<algorithm>
#include<cstdio>//
using namespace std;
const int N=1e5;
int n,m,K;
//n山峰,m猫,K人
long long a[N+5],b[N+5],g[N+5];
long long f[105][N+5];
long long dx(int x,int y,int i) {return x-y;
}
long long dy(int x,int y,int i) {return f[i][x]+g[x]-(f[i][y]+g[y]);
}
struct cat {long long c,d,h;
}t[N+5];
int cmp(cat x,cat y) {return x.h<y.h;
}//
int q[N+5];
int main() {cin>>n>>m>>K;for(int i=2;i<=n;i++) cin>>a[i];for(int i=1;i<=n;i++) b[i]=b[i-1]+a[i];for(int i=1;i<=m;i++) cin>>t[i].c>>t[i].d;for(int i=1;i<=m;i++) t[i].h=t[i].d-b[t[i].c];sort(t+1,t+1+m,cmp);for(int i=1;i<=m;i++) g[i]+=g[i-1]+t[i].h;// cout<<"***"<<endl;
// for(int i=1;i<=m;i++)
// cout<<t[i].h<<' '<<t[i].c<<' '<<t[i].d<<endl;
// cout<<"***"<<endl;
// cout<<"***"<<endl;
// for(int i=1;i<=m;i++) cout<<g[i]<<' ';
// cout<<endl;for(auto&i:f[0]) i=1e14;f[0][0]=0;for(int i=1;i<=K;i++) {int h=1,T=0; for(int j=1;j<=m;j++) {while(h<T&&dy(q[T],q[T-1],i-1)*dx(j-1,q[T],i-1)>=dy(j-1,q[T],i-1)*dx(q[T],q[T-1],i-1)) T--;q[++T]=j-1;while(h<T&&dy(q[h+1],q[h],i-1)<=t[j].h*dx(q[h+1],q[h],i-1)) h++;int k=q[h];f[i][j]=f[i-1][k]+(j-k)*t[j].h+g[k]-g[j];
// printf("f[%d %d]=f[%d %d]+%d=%d\n",i,j,i-1,k,t[j].h*(j-k)-(g[j]-g[k]),f[i][j]);}
// cout<<"i="<<i<<" ***"<<endl;
// for(int j=1;j<=m;j++)
// cout<<f[i][j]<<' ';
// cout<<endl;}cout<<f[K][m];
}
凸壳上二分
题解视频
转移还是: f i = min j = 0 i − 1 { f j + m ( b n − b j ) + a i ( b i − b j ) } f_i=\overset{i-1}{\underset{j=0}{\min}}\left\{f_j+m(b_n-b_j)+a_i(b_i-b_j)\right\} fi=j=0mini−1{fj+m(bn−bj)+ai(bi−bj)}
但是存在负数了,所以斜率不再是单调递增的,队头不再可以出队了。但是因为下凸壳斜率单调递增,我们可以在凸壳上二分。
int find(int i) {//返回最后一个斜率<a[i]的直线的右端点 if(h==t) return q[h];int l=h,r=t;while(l<r) {//左闭右闭int mid=l+r+1>>1;if(dy(q[mid],q[mid-1])<dx(q[mid],q[mid-1])*a[i]) l=mid;else r=mid-1;//如果mid=1,则会一直不满足条件,则r每次缩小一半,最后返回0,不会出错 }return q[l];
}
完整代码:
#include<algorithm>
#include<map>
#include<iostream>
using namespace std;
const int N=3e5;
long long a[N+5],b[N+5];
int q[N+5],h=1,t;
long long f[N+5];
int n;
long long m;
long long dx(int x,int y) {return b[x]-b[y];
}
long long dy(int x,int y) {return f[x]-m*b[x]-f[y]+m*b[y];
}
int find(int i) {//返回最后一个斜率<a[i]的直线的右端点 if(h==t) return q[h];int l=h,r=t;while(l<r) {int mid=l+r+1>>1;if(dy(q[mid],q[mid-1])<dx(q[mid],q[mid-1])*a[i]) l=mid;else r=mid-1;//如果mid=1,则会一直不满足条件,则r每次缩小一半,最后返回0,不会出错 }return q[l];
}
//int find(int i) {
// if(h==t) return q[h];
// int l=h-1,r=t+1;
// while(l+1<r) {
// int mid=l+r>>1;
// if(dy(q[mid],q[mid-1])<=a[i]*dx(q[mid],q[mid-1])) l=mid;
// else r=mid;
// }
// return q[l];
//}
int main() {cin>>n>>m;for(int i=1;i<=n;i++) (cin>>a[i]>>b[i]),a[i]+=a[i-1],b[i]+=b[i-1];for(int i=1;i<=n;i++) {while(h<t&&dy(i-1,q[t])*dx(q[t],q[t-1])<=dy(q[t],q[t-1])*dx(i-1,q[t])) t--;//若dx=0,则仅当dy为负数时有贡献,此时弹出队尾,不会出错 q[++t]=i-1;
// while(h<t&&sl(q[h],q[h+1])<=a[i]) h++;int j=find(i);f[i]=f[j]+m*(b[n]-b[j])+a[i]*(b[i]-b[j]);}cout<<f[n];
}
后记
于是皆大欢喜。