【数据结构】 七大排序详解(贰)——冒泡排序、快速排序、归并排序

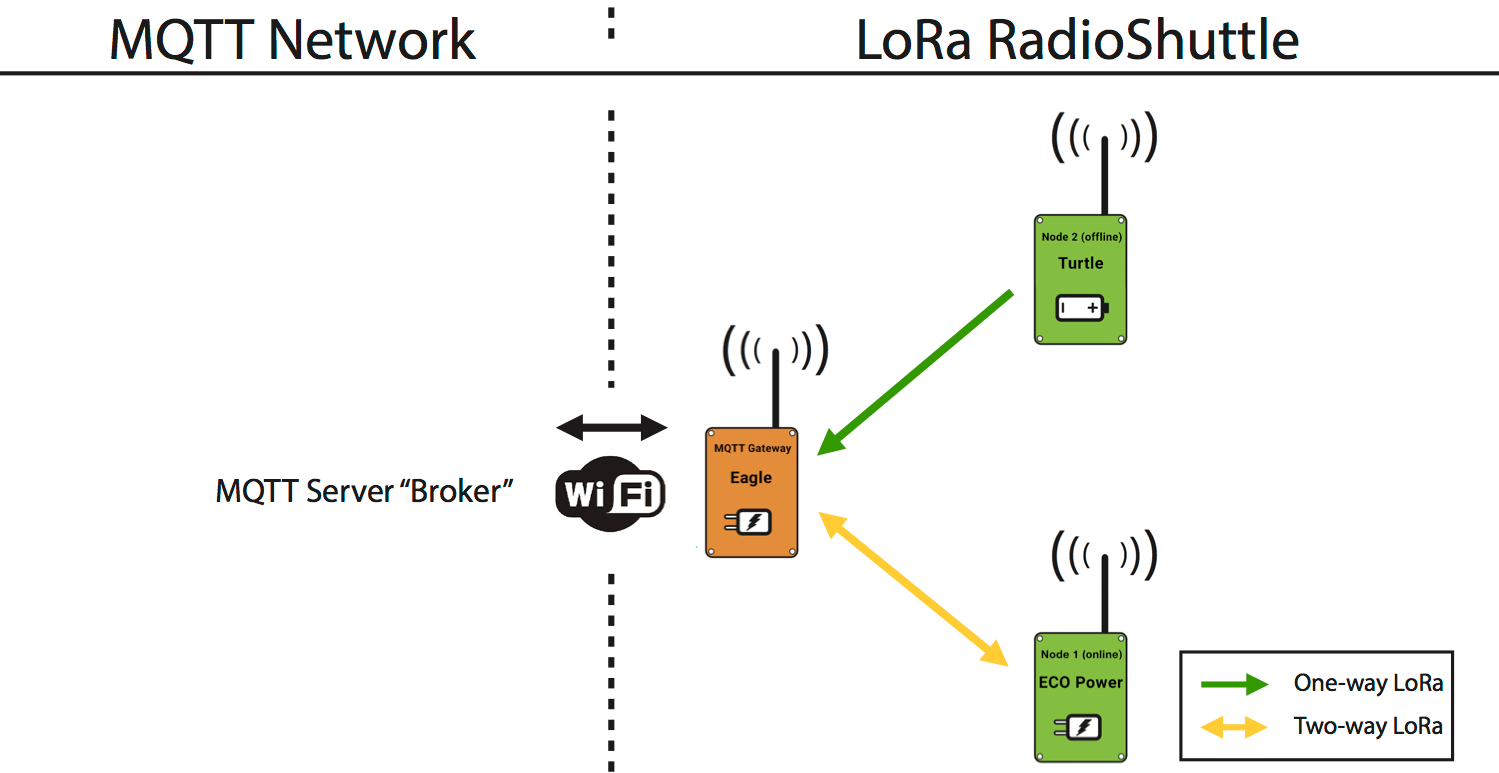
文章目录

  • ⚽冒泡排序
    • ⚾算法步骤
    • 🎨算法优化
    • 🥎代码实现：
    • 🏀冒泡排序的特性总结
  • 🧭快速排序
    • ⚽算法思路
      • 📌思路一（Hoare版）
      • 📌思路二（挖坑法）
      • 📌思路三（前后指针）
    • 🎨代码实现：
    • 🌳快速排序优化
      • 📌规模较小时的优化
      • 📌三数取中法
    • 🏀快速排序递归实现
      • 🚩代码实现：
    • 🎡快速排序特性总结
  • 🥎归并排序
    • ⚽基本思想
    • 🏀算法步骤
    • 🛫代码实现：
    • 😎递归实现归并排序
    • 🛬归并排序特性总结
    • 🌴海量数据的排序问题
  • 🐱‍🏍排序算法复杂度及稳定性分析
  • ⭕总结

⚽冒泡排序

==冒泡排序（Bubble Sort）==也是一种简单直观的排序算法。它重复地走访过要排序的数列，一次比较两个元素，如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢"浮"到数列的顶端。

⚾算法步骤

比较相邻的元素。如果第一个比第二个大，就交换他们两个。

对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。这步做完后，最后的元素会是最大的数。

针对所有的元素重复以上的步骤，除了最后一个。

持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

在这里插入图片描述

🎨算法优化

冒泡排序还有一种优化算法，就是立一个 flag，当在一趟序列遍历中元素没有发生交换，则证明该序列已经有序

直接返回就好

🥎代码实现：

    public  int[] bubbleSort(int[] arr) {int[] array = Arrays.copyOf(arr,arr.length);for(int i = 1;i < array.length ; i ++) {Boolean a = true;for(int j = 0; j < array.length - i; j++) {if(array[j] > array[j + 1]) {swap(array,j,j+1);a = false;}}if(a) {return array;}}return array;}private void swap (int[] arr,int m,int n) {int tmp = arr[m];arr[m] = arr[n];arr[n] = tmp;}

🏀冒泡排序的特性总结

  1. 冒泡排序是一种非常容易理解的排序

  2. 时间复杂度：O(N^2)

  3. 空间复杂度：O(1)

  4. 稳定性：稳定

  5. 什么时候最快
    当输入的数据已经是正序时（都已经是正序了，我还要你冒泡排序有何用啊）。

  6. 什么时候最慢
    当输入的数据是反序时（写一个 for 循环反序输出数据不就行了，干嘛要用你冒泡排序呢，我是闲的吗）。

🧭快速排序

快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法，其基本思想为：任取待排序元素序列中的某元素作为基准值，按照该排序码将待排序集合分割成两子序列，左子序列中所有元素均小于基准值，右子序列中所有元素均大于基准值，然后最左右子序列重复该过程，直到所有元素都排列在相应位置上为止

⚽算法思路

📌思路一（Hoare版）

步骤为：

  1. 选取基准值

  2. 从数组右->左找到比基准值小于或等于的值的下标

  3. 从数组右->左找到比基准值大于或等于的值的下标

  4. 交换这两下标的值

  5. 继续执行二操作，直到操作2与操作3相遇

  6. 将基准值放在相遇位置

如下图所示：

在这里插入图片描述

📌思路二（挖坑法）

步骤为：

  1. 选取基准值后，记录下基准值，假设该下标为空，相当于是个“坑”

  2. 从右->左找小于或等于基准值的值，就将该数放入坑中，然后该下标变为新的坑

  3. 从左->右找小于或等于基准值的值，就将该数放入坑中，然后该下标变为新的坑

  4. 回到步骤2继续执行，直到操作2与操作3所找数相同

  5. 将记录下的基准值放回坑里

图示如下：
在这里插入图片描述

📌思路三（前后指针）

步骤及其动图如下：
在这里插入图片描述

🎨代码实现：

    public int[] quickSort(int[] array) {int[] arr = Arrays.copyOf(array,array.length);int left = 0;int right = arr.length - 1;quick(arr,left,right);return arr;}private void quick(int[] array,int begin,int end) {if(begin >= end) {return;}int centre = partition1(array,begin,end);//int centre = partition2(array,begin,end);//int centre = partition3(array,begin,end);quick(array,centre + 1,end);quick(array,begin,centre - 1);}//挖坑法private  int partition1(int[] array,int left,int right) {int tmp = array[left];while (left < right) {while (left< right && array[right] >= tmp) {right--;}array[left] = array[right];while (left< right && array[left] <= tmp) {left++;}array[right] = array[left];}array[left] = tmp;return left;}//Hoare版private  int partition2(int[] array,int left,int right) {int tmp = array[left];int i = left;while (left < right) {while (left< right && array[right] >= tmp) {right--;}while (left< right && array[left] <= tmp) {left++;}swap(array,left,right);}swap(array,left,i);return left;}//前后指针法private int partition3(int[] array,int left,int right) {int prev = left ;int cur = left+1;while (cur <= right) {if(array[cur] < array[left] && array[++prev] != array[cur]) {swap(array,cur,prev);}cur++;}swap(array,prev,left);return prev;}private void swap (int[] arr,int m,int n) {int tmp = arr[m];arr[m] = arr[n];arr[n] = tmp;}

🌳快速排序优化

📌规模较小时的优化

每次递归的时候，数据都是再慢慢变成有序的

当数据量少且趋于有序的时候，我们可以直接使用插入排序进行优化

    private void quick(int[] array,int begin,int end) {if(begin >= end) {return;}if(end - begin < 20) {//插入排序//......return;}int centre = partition1(array,begin,end);//int centre = partition2(array,begin,end);//int centre = partition3(array,begin,end);quick(array,centre + 1,end);quick(array,begin,centre - 1);}

📌三数取中法

如果在选取基数时我们发现如果基数一边总是没有数，代码的执行次数会增加很多

所以我们的解决方法为：
选取数组第一个数、中间的数、和最后一个数，进行比较

三数中间的数作为每次的基数

寻找中间数代码如下：

    private  int midThree(int[] array,int left,int right) {int mid = (left + right) / 2;//6  8if (array[left] < array[right]) {if (array[mid] < array[left]) {return left;} else if (array[mid] > array[right]) {return right;} else {return mid;}} else {//array[left] > array[right]if (array[mid] < array[right]) {return right;} else if (array[mid] > array[left]) {return left;} else {return mid;}}}

使用如下：

    private  int partition1(int[] array,int left,int right) {int tmp = midThree(array,left,right);while (left < right) {while (left< right && array[right] >= tmp) {right--;}array[left] = array[right];while (left< right && array[left] <= tmp) {left++;}array[right] = array[left];}array[left] = tmp;return left;}//Hoare版private  int partition2(int[] array,int left,int right) {int tmp = midThree(array,left,right);int i = left;while (left < right) {while (left< right && array[right] >= tmp) {right--;}while (left< right && array[left] <= tmp) {left++;}swap(array,left,right);}swap(array,left,i);return left;}

🏀快速排序递归实现

实现思路：

  • 建立一个栈

  • 先让一组数据的起点入栈

  • 再让一组数据的终点出栈

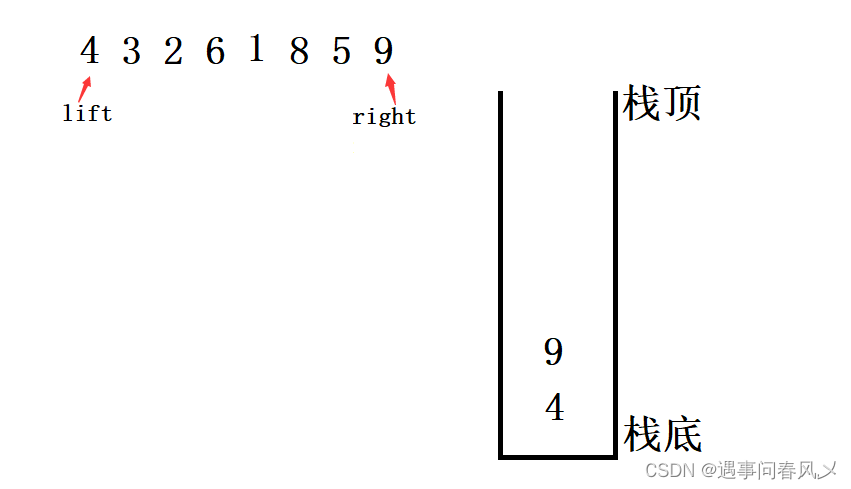
  • 在这里插入图片描述

  • 然后两次出栈，分别作为该数据的起点与终点

  • 然后经过我们上面所写的方法进行排序后

  • 再将两组数据进行入栈

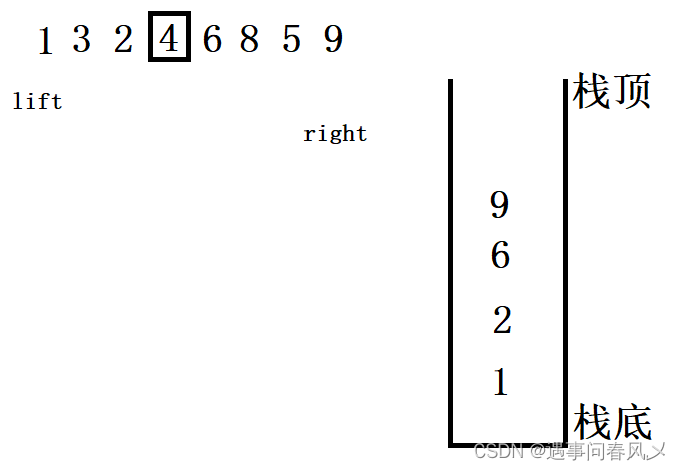
  • 在这里插入图片描述

  • 以此循环直到栈为空

🚩代码实现：

    //快速排序递归实现public int[] quickSortPlus(int[] array) {int[] arr = Arrays.copyOf(array,array.length);Deque<Integer> stack = new LinkedList<>();int left = 0;int right = array.length-1;int pivot = 0;stack.push(left);stack.push(right);while (!stack.isEmpty()) {right= stack.pop();left = stack.pop();pivot = partition(arr,left,right);if(pivot > left+1) {stack.push(left);stack.push(pivot-1);}if(pivot < right-1) {stack.push(pivot+1);stack.push(right);}}return arr;}private  int partition(int[] array,int left,int right) {int tmp = array[left];while (left < right) {while (left< right && array[right] >= tmp) {right--;}array[left] = array[right];while (left< right && array[left] <= tmp) {left++;}array[right] = array[left];}array[left] = tmp;return left;}

🎡快速排序特性总结

  1. 快速排序整体的综合性能和使用场景都是比较好的，所以才敢叫快速排序

  2. 时间复杂度：O(N*logN)
    在这里插入图片描述

  3. 空间复杂度：O(logN)

  4. 稳定性：不稳定

🥎归并排序

⚽基本思想

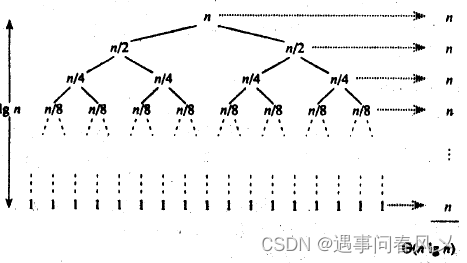
归并排序（MERGE-SORT）是建立在归并操作上的一种有效的排序算法,该算法是采用分治法（Divide and
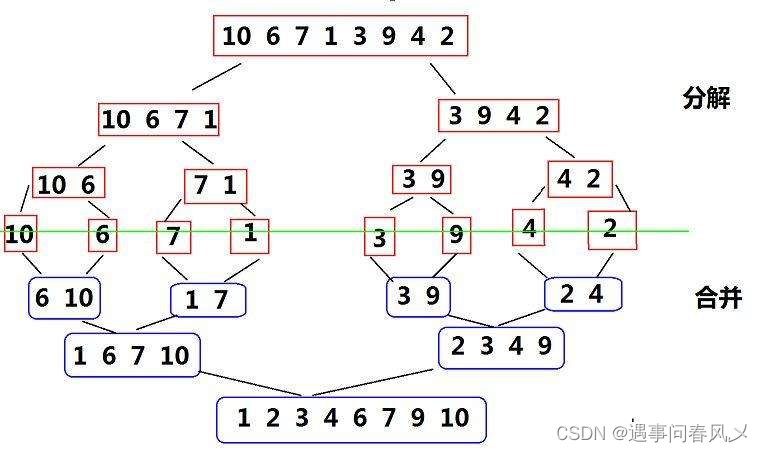
Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。 归并排序核心步骤：
在这里插入图片描述

🏀算法步骤

  1. 申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列；

  2. 设定两个指针，最初位置分别为两个已经排序序列的起始位置；

  3. 比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置；

  4. 重复步骤 3 直到某一指针达到序列尾；

  5. 将另一序列剩下的所有元素直接复制到合并序列尾。

在这里插入图片描述

🛫代码实现：

    public  void mergeSort1(int[] array) {mergeSortFunc(array,0,array.length-1);}private  void mergeSortFunc(int[] array,int left,int right) {if(left >= right) {return;}int mid = (left+right) / 2;mergeSortFunc(array,left,mid);mergeSortFunc(array,mid+1,right);merge(array,left,right,mid);}private  void merge(int[] array,int start,int end,int mid) {int s1 = start;//int e1 = mid;int s2 = mid+1;//int e2 = end;int[] tmp = new int[end-start+1];int k = 0;//tmp数组的下标while (s1 <= mid && s2 <= end) {if(array[s1] <= array[s2]) {tmp[k++] = array[s1++];}else {tmp[k++] = array[s2++];}}while (s1 <= mid) {tmp[k++] = array[s1++];}while (s2 <= end) {tmp[k++] = array[s2++];}for (int i = 0; i < tmp.length; i++) {array[i+start] = tmp[i];}}

😎递归实现归并排序

public static void mergeSort(int[] array) {int gap = 1;while (gap < array.length) {// i += gap * 2 当前gap组的时候，去排序下一组for (int i = 0; i < array.length; i += gap * 2) {int left = i;int mid = left+gap-1;//有可能会越界if(mid >= array.length) {mid = array.length-1;}int right = mid+gap;//有可能会越界if(right>= array.length) {right = array.length-1;}merge(array,left,right,mid);}//当前为2组有序  下次变成4组有序gap *= 2;}}private  void merge(int[] array,int start,int end,int mid) {int s1 = start;//int e1 = mid;int s2 = mid+1;//int e2 = end;int[] tmp = new int[end-start+1];int k = 0;//tmp数组的下标while (s1 <= mid && s2 <= end) {if(array[s1] <= array[s2]) {tmp[k++] = array[s1++];}else {tmp[k++] = array[s2++];}}while (s1 <= mid) {tmp[k++] = array[s1++];}while (s2 <= end) {tmp[k++] = array[s2++];}for (int i = 0; i < tmp.length; i++) {array[i+start] = tmp[i];}}

🛬归并排序特性总结

  1. 归并的缺点在于需要O(N)的空间复杂度，归并排序的思考更多的是解决在磁盘中的外排序问题。

  2. 时间复杂度：O(N*logN)

  3. 空间复杂度：O(N)

  4. 稳定性：稳定

🌴海量数据的排序问题

外部排序：排序过程需要在磁盘等外部存储进行的排序

前提：内存只有 1G，需要排序的数据有 100G

因为内存中因为无法把所有数据全部放下，所以需要外部排序，而归并排序是最常用的外部排序

  1. 先把文件切分成 200 份，每个 512 M

  2. 分别对 512 M 排序，因为内存已经可以放的下，所以任意排序方式都可以

  3. 进行 2路归并，同时对 200 份有序文件做归并过程，最终结果就有序了

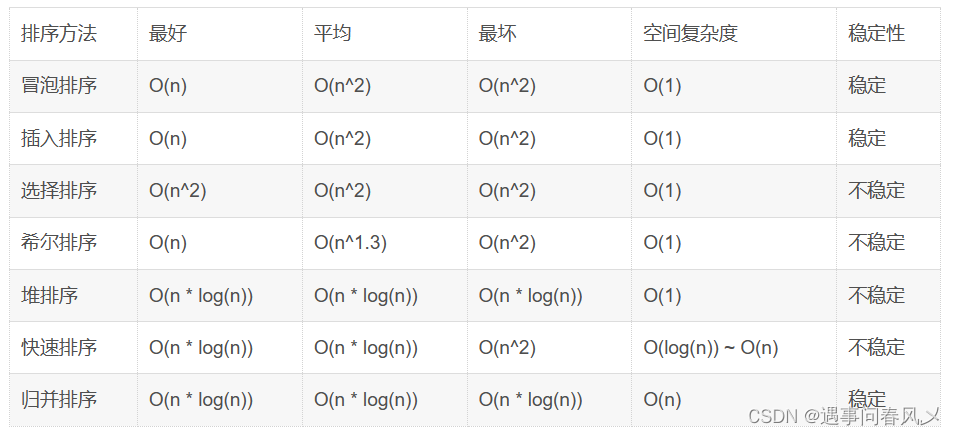
🐱‍🏍排序算法复杂度及稳定性分析

在这里插入图片描述
在这里插入图片描述

⭕总结

关于《【数据结构】 七大排序详解(贰)——冒泡排序、快速排序、归并排序》就讲解到这儿，感谢大家的支持，欢迎各位留言交流以及批评指正，如果文章对您有帮助或者觉得作者写的还不错可以点一下关注，点赞，收藏支持一下！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.hqwc.cn/news/102903.html

如若内容造成侵权/违法违规/事实不符，请联系编程知识网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

【MySQL系列】MySQL的事务管理的学习（一）_ 事务概念 | 事务操作方式 | 事务隔离级别

【MySQL系列】MySQL的事务管理的学习（一）_ 事务概念 | 事务操作方式 | 事务隔离级别

「前言」文章内容大致是MySQL事务管理。 「归属专栏」MySQL 「主页链接」个人主页 「笔者」枫叶先生(fy) 目录 一、事务概念二、事务的版本支持三、事务提交方式四、事务常见的操作方式4.1 事务正常操作4.2 事务异常验证 五、事务隔离级别5.1 查看与设置隔离性5.2 读未提交&…
阅读更多...
c语言实训心得3篇集合

c语言实训心得3篇集合

c语言实训心得体会一&#xff1a; 在这个星期里&#xff0c;我们专业的学生在专业老师的带领下进行了c语言程序实践学习。在这之前&#xff0c;我们已经对c语言这门课程学习了一个学期&#xff0c;对其有了一定的了解&#xff0c;但是也仅仅是停留在了解的范围&#xff0c;对里…
阅读更多...
软件测试/测试开发丨Python 深拷贝与浅拷贝

软件测试/测试开发丨Python 深拷贝与浅拷贝

点此获取更多相关资料 本文为霍格沃兹测试开发学社学员学习笔记分享 原文链接&#xff1a;https://ceshiren.com/t/topic/27327 深拷贝与浅拷贝 浅拷贝&#xff1a;有4中实现方法&#xff1a;对象本身的copy方法&#xff0c;工厂方法&#xff0c;切片以及copy模块的copy方法。…
阅读更多...
记录aardio和Pythonl联动，为python做界面、做单exe文件的几个知识点

记录aardio和Pythonl联动，为python做界面、做单exe文件的几个知识点

关于aardio的几个目录的说明 如果要aardio创建python关联程序，强烈建议新建工程向导中选择“窗口程序”+python来生成，会自动建立好目录，十分方便。 写好的python脚本或工程，直接放到py目录中，aardio中可以直接import导入该目录中的python模块，无需带目录，类似： aar…
阅读更多...
vue3：5、组合式API-reactive和ref函数

vue3：5、组合式API-reactive和ref函数

<script setup> /* reactive接收一个对象类型的数据&#xff0c;返回一个响应式的对象 *//*** ref:接收简单类型或复杂类型&#xff0c;返回一个响应式对象* 本质&#xff1a;是在原有传入数据的基础上&#xff0c;外层报了一层对象&#xff0c;包成了复杂类型* 底层&…
阅读更多...
vue前后端端口不一致解决方案

vue前后端端口不一致解决方案

在config index.js文件中 引入如下代码即可 const path require(path) const devEnv require(./dev.env) module.exports {dev: {// PathsassetsSubDirectory: static,assetsPublicPath: /,proxyTable: devEnv.OPEN_PROXY false ? {} : {/api: {target: http://localhos…
阅读更多...
接口自动化测试总结

接口自动化测试总结

一、什么项目适合做自动化测试&#xff1f; 软件需求变动不频繁 测试脚本的稳定性决定了自动化测试的维护成本。如果软件需求变动过于频繁&#xff0c;测试人员需要根据变动的需求来更新测试用例以及相关的测试脚本&#xff0c;而脚本的维护本身就是一个代码开发的过程&#x…
阅读更多...
【web开发】4.JavaScript与jQuery

【web开发】4.JavaScript与jQuery

提示&#xff1a;文章写完后&#xff0c;目录可以自动生成&#xff0c;如何生成可参考右边的帮助文档 文章目录 一、JavaScript与jQuery二、JavaScript常用的基本功能1.插入位置2.注释3.变量4.数组5.滚动字符 三、jQuery常用的基本功能1.引入jQuery2.寻找标签3.val、text、appe…
阅读更多...
yo！这里是进程控制

yo！这里是进程控制

目录 前言 进程创建 fork()函数 写时拷贝 进程终止 退出场景 退出方法 进程等待 等待原因 等待方法 1.wait函数 2.waitpid函数 等待结果&#xff08;status介绍&#xff09; 进程替换 替换原理 替换函数 进程替换例子 shell简易实现 后记 前言 学习完操作…
阅读更多...
校园二手物品交易系统微信小程序设计

校园二手物品交易系统微信小程序设计

系统简介 本网最大的特点就功能全面&#xff0c;结构简单&#xff0c;角色功能明确。其不同角色实现以下基本功能。 服务端 后台首页&#xff1a;可以直接跳转到后台首页。 用户信息管理&#xff1a;管理所有申请通过的用户。 商品信息管理&#xff1a;管理校园二手物品中…
阅读更多...
2023-9-8 求组合数(三)

2023-9-8 求组合数(三)

题目链接&#xff1a;求组合数 III #include <iostream> #include <algorithm>using namespace std;typedef long long LL;int p;int qmi(int a, int k) {int res 1;while(k){if(k & 1) res (LL) res * a % p;k >> 1;a (LL) a * a % p;}return res; }…
阅读更多...
Android MQTT：实现设备信息上报与远程控制

Android MQTT：实现设备信息上报与远程控制

Android MQTT&#xff1a;实现设备信息上报与远程控制 1. 介绍 1.1 MQTT是什么&#xff1f; MQTT&#xff08;Message Queuing Telemetry Transport&#xff09;是一种轻量级的消息传输协议&#xff0c;最初由IBM开发&#xff0c;用于连接远程设备与服务器之间的通信。它在物…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023