前言
之前遇到过几次,后面稀里糊涂的解决了。今天详细记录一下,可能不全或有些错误,还请各位指正。
你要启动一个类的话首先要有类。
在这里,类有两种,
- 一个是带包名(package)的
- 还有一个是没包名(package)的
但都需要有一个公共的静态 main方法,不然怎么也启动不了。
一、不带包名的
我们以一个路径为E:\demo\Welcome.java的例子导入
// Welcome.java
public class Welcome {public static void main(String[] args) {System.out.println("Welcome to learn Java!");}
}

1、编译运行
在终端中,编译运行成功的正确操作是:
- 进入类所在的文件
E:\demo

- 使用
javac Welcome.java进行编译生成class文件
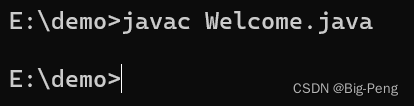

- 使用
java Welcome运行成功
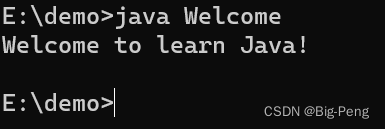
2、注意事项
-
如果手工输人源程序,一定要注意正确地输人大小写。例如,类名为welcome,而不是welcome或WELCOME。
-
编译器需要-一个文件名(Welcome.java), 而运行程序时,只需要指定类名(Welcome), 不要带扩展名.java 或.class。
-
如果看到诸如
Bad command or file name或javac:command not found之类的消息,就要返回去反复检查安装是否有问题,特别是可执行路径的设置。 -
如果javac报告了一个错误,指出无法找到Welcome.java,就应该检查目录中是否存在。
- 在Linux环境下,检查Welcome.java是否以正确的大写字母开头。
- 在Windows环境下,使用命令dir,而不要使用图形浏览器具。有些文本编辑器(特别是Notepad)会在每个文件名后面添加扩展名.txt。如果使用Notepad编辑Welcome.java,实际上会把它保存为Welcome.java.txt。
3、java. lang.NoClassDefFoundError错误的原因
-
如果收到关于welcome (W为小写)的错误消息
应该重新执行命令: java Welcome(W为大写)。记住,Java区分大小写。
-
如果收到有关demo/java的错误信息
说明你错误地键人了java Welcome.java , 应该重新执行命令java Welcome。
-
如果键入java Welcome, 而虚拟机没有找到Welcome类,就应该检查是否有人设置了系统的
CLASSPATH环境变量(将这个变量设置为全局并不是提倡的做法,然而,Windows中有些比较差的软件安装程序确实会这样做)。可以像设置PATH环境变量–样设CLASSPATH,不过这里将删除这个设置。
二、带包的
在demo文件夹中新建一个Mypackage文件夹里面定义一个Welcome2类。E:\demo\MyPackage\Welcome2.java
// Welcome2.java
package MyPackage;public class Welcome2 {public static void main(String[] args) {System.out.println("Welcome to learn Java222!");}
}
1、编译运行
-
命令行进入当前文件夹

-
使用
javac Welcome2.java完成编译,生成class文件
-
使用
java命令运行程序-
这里与不带包的类运行有所不同
-
在当前类文件夹下使用
java Welcome2会报找不到类的错误(我不知道为什么)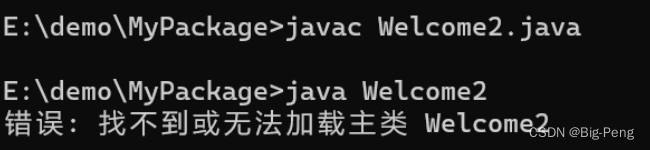
-
此时应该退回package所在的目录,这里是
demo文件夹使用java运行,但是有由一些问题:使用
java MyPackage\Welcome2(tab自动补全的)也会报错(我也不明白-_-!)使用
java MyPackage/Welcome2运行成功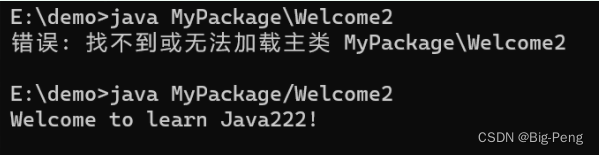
-
-
直接在package所在目录下编译也是可以的

2、错误
其他错误原因同不带package的类。
三、总结
-
不带package的类
直接在类所在目录下编译运行即可,常见的错误为类不存在、类名写错、环境配置……
-
带package的类
在package所在目录下编译运行,注意路径不要用tab键生成的
\符,而是用/,否则也找不到。不清楚是为什么,欢迎大神评论指出。