目录
1、贝叶斯算法
2、朴素贝叶斯算法
3、先验概率和后验概率
4、⭐机器学习中的贝叶斯公式
5、文章分类中的贝叶斯
6、拉普拉斯平滑系数
6.1、介绍
6.2、公式
7、API
8、示例
8.1、分析
8.2、代码
8.3、⭐预测流程分析
🍃作者介绍:准大三本科网络工程专业在读,阿里云专家博主,专注于Java领域学习,擅长web应用开发、数据结构和算法,初步涉猎Python人工智能开发。
🦅主页:@逐梦苍穹
⭐分类算法系列①:初识概念
⭐分类算法系列②:KNN(K-近邻)算法
⭐分类算法系列③:模型选择与调优 (Facebook签到位置预测)
🍁您的三连支持,是我创作的最大动力🌹

首先介绍贝叶斯算法,再介绍朴素贝叶斯,朴素贝叶斯是贝叶斯的特殊情况。
1、贝叶斯算法
贝叶斯算法是基于贝叶斯定理的一类算法,用于从已知的条件概率中推断出未知事件的概率。贝叶斯定理是一个描述联合概率分布的数学公式,其形式如下:
其中:
- P(A∣B) 表示在已知事件 B 发生的情况下事件 A 发生的概率(后验概率)。
- P(B∣A) 表示在已知事件 A 发生的情况下事件 B 发生的概率。
- P(A) 和 P(B) 分别表示事件 A 和事件 B 的先验概率。
贝叶斯算法的应用范围广泛,包括垃圾邮件过滤、文本分类、推荐系统等。通过不断地更新先验概率和计算后验概率,贝叶斯算法可以根据新的证据不断更新对未知事件的概率估计。
2、朴素贝叶斯算法
朴素贝叶斯算法是贝叶斯算法的一种特例,用于分类问题。它假设特征之间相互独立,从而简化了计算过程。尽管这个假设通常并不成立,但朴素贝叶斯算法在很多实际应用中表现出色。
朴素贝叶斯算法的基本思想是基于贝叶斯定理,通过计算后验概率来判断给定输入数据属于不同的类别。在分类问题中,输入数据被表示为特征向量,而类别即为需要预测的目标类别。朴素贝叶斯分类器根据训练数据学习类别的概率分布,然后根据输入特征计算后验概率,选择概率最高的类别作为预测结果。
朴素贝叶斯算法具有简单、高效的特点,适用于文本分类、垃圾邮件过滤、情感分析等任务。
尽管其假设特征之间独立的前提在现实中不一定成立,但在许多情况下,朴素贝叶斯算法依然能够取得很好的分类效果。
3、先验概率和后验概率
先验概率(Prior Probability)和后验概率(Posterior Probability)都是贝叶斯定理中的概念,用于描述在已知或考虑了一些信息或条件的情况下,事件发生的概率。
- 先验概率: 先验概率是在考虑任何新信息之前,根据以往的经验或已有的知识,对事件发生概率的主观估计。它表示在没有额外信息的情况下,事件发生的概率。在贝叶斯定理中,先验概率被表示为 P(A),其中 A 表示某个事件。
- 后验概率: 后验概率是在考虑了新信息或额外条件后,对事件发生概率进行更新的概率。它表示在已知一些条件或信息的情况下,事件发生的概率。在贝叶斯定理中,后验概率被表示为 P(A∣B),其中 A 表示某个事件,B 表示已知的条件或信息。
贝叶斯定理描述了如何根据已知的条件和先验概率计算后验概率,即如何将新信息融入到概率估计中。这个过程可以帮助我们更准确地估计事件的概率,尤其是在有限的数据或信息下。在机器学习和统计中,贝叶斯定理和先验、后验概率的概念经常被用于构建分类器、预测模型和概率推断。
4、⭐机器学习中的贝叶斯公式
原理同普遍条件下的公式肯定是的,但是表现形式可以略有不同。
在机器学习中,特别是在朴素贝叶斯分类器中,贝叶斯公式的形式通常如下:
其中:
是给定输入数据 X,在类别
下发生的后验概率,表示为对于给定数据 X,它属于类别
的概率。
是在类别
下,输入数据 X 发生的条件概率,表示为给定类别
下输入数据 X 的概率。
是类别
的先验概率,表示在没有任何信息的情况下,数据属于类别
的概率。
是输入数据
的边缘概率,表示数据
发生的概率。
在朴素贝叶斯算法中,假设特征之间是独立的(朴素假设),因此可以将 表示为各个特征的条件概率的乘积,即
。
表示第
个特征.
这个公式用于计算在给定输入数据 X 的情况下,属于各个类别 的后验概率。
在分类问题中,我们可以选择具有最高后验概率的类别作为预测的类别。
5、文章分类中的贝叶斯
公式分为三个部分(其中C可以是不同类别):
- P(C):每个文档类别的概率(某文档类别数/总文档数量)
- P(W│C):给定类别下特征(被预测文档中出现的词)的概率
- 计算方法:P(F1│C)=Ni/N(训练文档中去计算)
- Ni为该F1词在C类别所有文档中出现的次数
- N为所属类别C下的文档所有词出现的次数和
- 计算方法:P(F1│C)=Ni/N(训练文档中去计算)
- P(F1,F2,…) 预测文档中每个词的概率
6、拉普拉斯平滑系数
6.1、介绍
拉普拉斯平滑(Laplace Smoothing),也称为加一平滑(Add-One Smoothing)或修正的拉普拉斯法则,是一种用于解决概率估计中的零概率问题的技术。它主要应用于朴素贝叶斯分类器等机器学习和自然语言处理任务中。
在统计学和概率论中,当我们根据已有数据估计事件的概率时,有时候可能会遇到某些事件在训练数据中没有出现,导致估计出的概率为零。这可能会在实际应用中引起问题,例如在贝叶斯分类器中,如果某个特征值在某个类别中未见过,就会导致整个分类概率为零。
拉普拉斯平滑通过为每个可能的特征值添加一个平滑因子,解决了这个问题。平滑因子通常是1,所以也称为加一平滑。它的基本思想是在所有可能的特征值上增加一个计数,使得每个特征值至少出现一次,从而避免零概率的问题。
在朴素贝叶斯分类器中,拉普拉斯平滑应用于计算条件概率。对于每个特征,都会将计数值加1,同时对可能的特征值总数进行加法平滑。这样,在计算后验概率时,就可以避免分子为零的情况。
拉普拉斯平滑的使用使得概率估计更稳定,尤其是在数据量有限的情况下。然而,这种平滑也可能引入一定的偏差,因为它会均匀地将概率分布平移,但在实际应用中,这种偏差通常是可以接受的。
6.2、公式
平滑后的条件概率:
参数解释:
表示在类别
下特征值
出现的次数。
表示在类别
下的样本总数。
表示特征
可能的取值数量(例如为训练文档中出现的特征词个数)
这个公式表示了在计算平滑后的条件概率时,为每个特征值 都加上了一个平滑因子,以确保每个特征值至少出现一次,避免零概率的情况。
7、API
sklearn.naive_bayes.MultinomialNB(alpha = 1.0)
朴素贝叶斯分类
alpha:拉普拉斯平滑系数
8、示例

8.1、分析
代码实现的步骤如下:
- 分割数据集
- tfidf进行的特征抽取
- 朴素贝叶斯预测
8.2、代码
# -*- coding: utf-8 -*-
# @Author:︶ㄣ释然
# @Time: 2023/9/1 11:00
from sklearn.datasets import fetch_20newsgroups # 20类新闻分类
from sklearn.feature_extraction.text import TfidfVectorizer # TF-IDF特征提取
from sklearn.model_selection import train_test_split # 训练集划分
from sklearn.naive_bayes import MultinomialNB # 多项式朴素贝叶斯分类器'''
sklearn.naive_bayes.MultinomialNB(alpha = 1.0)朴素贝叶斯分类alpha:拉普拉斯平滑系数
'''
def naiveBayes():"""朴素贝叶斯对新闻数据集进行预测"""# 获取新闻的数据,20个类别news = fetch_20newsgroups(subset='all')# 进行数据集分割x_train, x_test, y_train, y_test = train_test_split(news.data, news.target, test_size=0.3)# 对于文本数据,进行特征抽取tf = TfidfVectorizer()x_train = tf.fit_transform(x_train)# 这里打印出来的列表是:训练集当中的所有不同词的组成的一个列表print(tf.get_feature_names())# print(x_train.toarray())# 不能调用fit_transform# TF-IDF 特征抽取过程中,模型已经通过 x_train 学习了词汇表和特征权重,# 因此在处理测试集时只需要进行转换操作,而不再需要重新拟合模型x_test = tf.transform(x_test)# estimator估计器流程mlb = MultinomialNB(alpha=1.0)mlb.fit(x_train, y_train)# 进行预测y_predict = mlb.predict(x_test)print("预测每篇文章的类别:", y_predict[:100])print("真实类别为:", y_test[:100])print("预测准确率为:", mlb.score(x_test, y_test))if __name__ == '__main__':naiveBayes()实现结果:
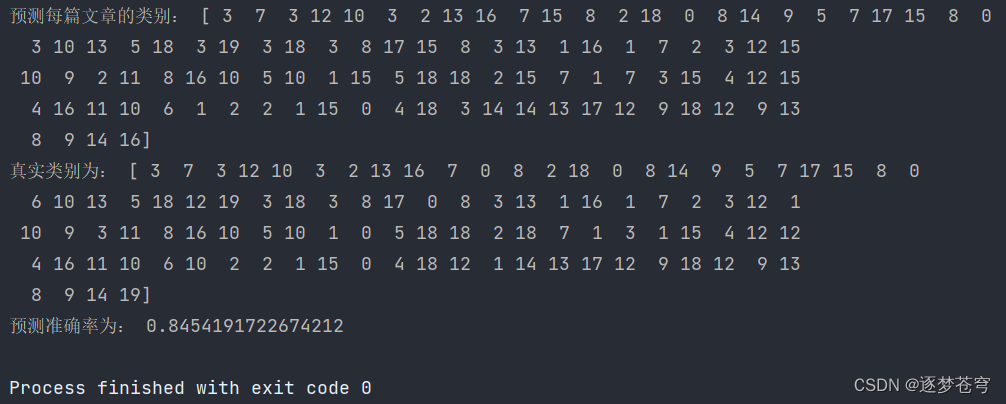
在代码中,有一段是:
![]()
这部分不能调用fit_transform():
TF-IDF 特征抽取过程中,模型已经通过 x_train 学习了词汇表和特征权重,
因此在处理测试集时只需要进行转换操作,而不再需要重新拟合模型
8.3、⭐预测流程分析
贝叶斯算法(包括朴素贝叶斯算法)在文本分类中的预测过程涉及计算后验概率,以确定最可能的类别。下面是详细的预测过程说明:
- 特征提取:首先,文本数据需要经过特征提取的过程,将文本转换为数字化的特征向量。在文本分类中,常用的特征表示方法是 TF-IDF(Term Frequency-Inverse Document Frequency)。
- 计算先验概率:对于每个类别
,需要计算它在训练数据中出现的概率,即先验概率
。这可以通过统计训练数据中属于类别
的样本数量除以总样本数量来得到。
- 计算条件概率:对于每个特征
,需要计算在给定类别
的情况下特征值
出现的概率,即条件概率
。这可以通过先前提到的拉普拉斯平滑后的条件概率公式来计算。
- 计算后验概率:对于给定的文本
,需要计算它在每个类别下的后验概率
,表示在已知文本特征的情况下属于类别
的概率。根据贝叶斯定理,后验概率可以表示为:
- 其中,
是在类别
下文本特征
出现的概率,可以根据特征独立性假设进行计算:
- -
是先验概率,
- -
是文本特征
出现的概率。
- 其中,
- 决策规则:选择具有最高后验概率的类别作为预测结果。即对于给定的文本
,选择满足
的类别
。