算法通关村第十九关：青铜-动态规划是怎么回事

青铜挑战-动态规划是怎么回事

动态规划（简称DP，Dynamic Programming）：最热门、最重要的算法之一。面试中大量出现，整体偏难。

1. 热身：重复计算和记忆化搜索（如何说一万次"我爱你"）

举例：看谁说更多的我爱你

class FibonacciTest:def __init__(self):self.count = 0def main(self, n):self.fibonacci(n)print(f"n: {n}, count: {self.count}")def fibonacci(self, n):print("我爱你")self.count += 1if n == 0:return 1elif n == 1 or n == 2:return nelse:return self.fibonacci(n - 1) + self.fibonacci(n - 2)if __name__ == '__main__':for i in range(32):FibonacciTest().main(i)

斐波那契数列，重复打印 “我爱你”
n=20时，count=13529；n=30时，count=1664079

n=30时，count高达160多万，因为里面存在大量的重复计算，数越大，重复越多。

n=8时，结构如下
在这里插入图片描述

计算 f(8) 时，f(6)、f(5)等需要重复计算，这就是重叠子问题

优化：
主要问题是很多数据到会频繁重复计算
将计算的结果保存到一个一维数组中，arr[n] = f(n)
执行的时候如果某个位置已经被计算出来就更新对应位置的数组值，下次计算的时候可直接读取

记录化搜索
在执行递归之前先查数组看是否被计算过，如果重复计算了，就直接读取，这就叫记忆化搜索

class FibonacciTest:def __init__(self):self.count = 0self.arr = []def main(self, n):self.arr = [-1] * (n + 1)self.fibonacci(n)print(f"n: {n}, count: {self.count}")def find_in_arr(self, n):return self.arr[n] if 0 <= n < len(self.arr) else -1def fibonacci(self, n):# print("我爱你")self.count += 1if n == 1 or n == 2:self.arr[n] = nreturn nelif self.arr[n] != -1:return self.arr[n]else:self.arr[n] = self.fibonacci(n - 1) + self.fibonacci(n - 2)return self.arr[n]if __name__ == '__main__':FibonacciTest().main(20)

n=20时，count=37；n=30时，count=57。
递归计算大为减少

2. 路径连环炮

本部分通过多个路径相关的问题来解释和分析DP

2.1 第一炮：基本问题-统计路径总数

LeetCode62
https://leetcode.cn/problems/unique-paths/

思路分析

本题是经典的递归问题

  • 从起点开始的每一个位置，要么向右，要么向下
  • 向右和向下都将导致剩下的区间减少一列或者一行
  • 每个区间都可以继续以当前点为起点继续上述操作，所以这是一个递归的过程

在这里插入图片描述

分析3x2矩阵
在这里插入图片描述

分析3x3矩阵
在这里插入图片描述

分析可以看出，对于一个m x n的矩阵，求路径总数的方法 search(m, n) = search(m-1, n) + search(m, n-1)

对于上述过程，也可以用二叉树表示出来，以3x3矩阵为例
在这里插入图片描述

总的路径就是叶子结点数，图中有6个，这与二叉树的递归遍历本质上是一样的

代码实现

class Solution:def uniquePaths(self, m: int, n: int) -> int:if m == 1 or n == 1:return 1return self.uniquePaths(m - 1, n) + self.uniquePaths(m, n - 1)if __name__ == '__main__':print(Solution().uniquePaths(3, 2))

注：功能没有问题，LeetCode上提交，判断超时了

2.2 第二炮：使用二维数组优化递归

在第一炮中，存在重复计算的问题，可以结合二维数组实现记忆化搜索

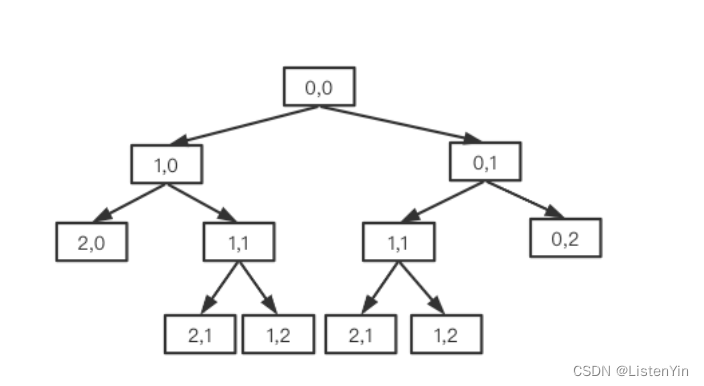
在这里插入图片描述

从数可以看到，在递归的过程中，存在重复计算的情况
例如 {1,1} 出现了两次，如果m=n，{1,0} 和 {0,1}的后续计算也是一样的
从二维数组的角度，例如在位置(1,1)处，不管是从(0,1)还是(1,0)到来，接下来都会产生2种走法，因此不必每次都重新遍历

在这里插入图片描述

可以采取一个二维数组来进行记忆化搜索

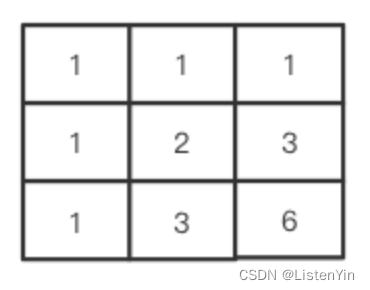
在这里插入图片描述

每个格子的数字：表示从起点开始到达当前位置有几种方式

  • 第1行和第1列都是1
  • 其他格子的值是其左侧和上侧格子数字之和 f[i][j] = f[i-1][j] + f[i][j-1]

在这里插入图片描述

在这里插入图片描述

代码实现

class Solution:def uniquePaths(self, m: int, n: int) -> int:arr = [[-1] * n for _ in range(m)]for i in range(m):for j in range(n):if i == 0 or j == 0:arr[i][j] = 1else:arr[i][j] = arr[i - 1][j] + arr[i][j - 1]return arr[m - 1][n - 1]

2.3 第三炮：滚动数组-用一维数组代替二维数组

上面的缓存空间使用的二维数组，占空间太大；可以使用滚动数组来优化此问题

滚动数组

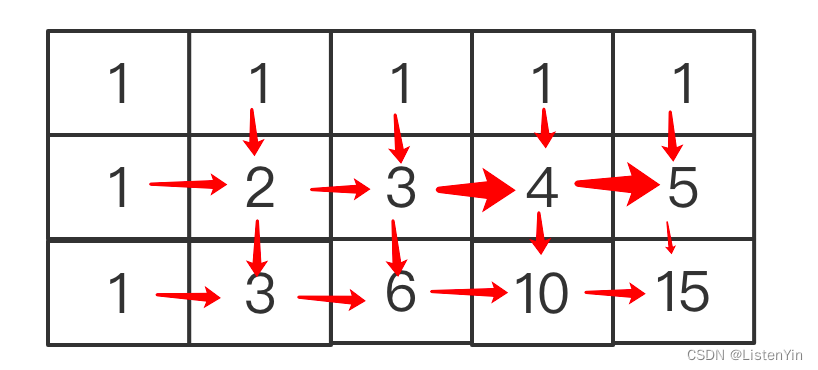
在这里插入图片描述

  • 第1行和第1列都是1
  • 每个位置都是其左侧和上方的格子之和

以上可以简化为一个大小为n的一维数组来解决

  1. 遍历数组，将数组所有元素赋值为1，[1,1,1,1,1]
  2. 再次遍历数组，除了第1个，后面每个位置值=原始值+前一个位置值，[1,2,3,4,5]
  3. 再次遍历数组，除了第1个，后面每个位置值=原始值+前一个位置值，[1,3,6,10,15]
  4. 继续循环，循环m次
    此处3*5，m=3，循环3次，输出最后的15为结果

上面这几个一维数组拼接起来就是原先的二维数组

这种反复更新数组的策略就是滚动数组，计算公式 dp[j] = dp[j] + dp[j-1]

代码实现

class Solution:def uniquePaths(self, m: int, n: int) -> int:arr = [1] * nfor i in range(1, m):for j in range(1, n):arr[j] = arr[j] + arr[j - 1]return arr[-1]

总结

本题涵盖了DP里的多个方面，比如重复子问题、记忆化搜索、滚动数组等等
这就是最简单的动态规划了，只不过我们这里的规划是 dp[j] = dp[j] + dp[j-1]，不用进行复杂的比较和计算

这个题目非常重要，对后面理解递归、动态规划等算法有非常大的作用

2.4 第四炮：题目拓展-最小路径和

上面的题目（LeetCode62）还有个重要的问题体现的不明显：最优子结构

LeetCode64
https://leetcode.cn/problems/minimum-path-sum/

思路分析

这道题目就是在上面题目的基础上，增加了路径成本的概念。

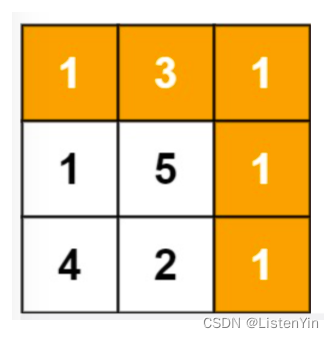
在这里插入图片描述

由于题目限定只能 往下 或者 往右，可以按照当前位置可由哪些位置移动过来进行分析

  • 通过 往下 移动过来，f[i][j] = f[i-1][j] + grid[i][j]
  • 通过 往右 移动过来，f[i][j] = f[i][j-1] + grid[i][j]
  • 通过 往下 或者 往右 移动过来，f[i][j] = min(f[i-1][j], f[i][j-1]) + grid[i][j]

二维数组的更新过程如下
在这里插入图片描述

引入新概念

状态与状态转移方程
状态：就是下面表格更新到最后的二维数组（？不太理解，简单的就是状态转移方程计算出来的值）

状态转移方程：通过前面格子状态计算后面格子状态的公式就叫状态转移方程

数组表达：
f[i][j] 从(0,0)开始到达位置(i,j)的最小路径成本总和，f[m-1][n-1]就是我们最终的答案

起始状态 f[0][0] = grid[0][0]

状态转移方程
f[i][j] = min(f[i-1][j], f[i][j-1]) + grid[i][j]

在这里插入图片描述

注：确定状态转移方程就是要找递推关系，通常我们会从分析首尾两端的变化规律入手

代码实现

class Solution:def minPathSum(self, grid: List[List[int]]) -> int:m, n = len(grid), len(grid[0])arr = [[0] * n for _ in range(m)]for i in range(m):for j in range(n):if i == 0 and j == 0:arr[i][j] = grid[i][j]elif i == 0:arr[i][j] = arr[i][j - 1] + grid[i][j]elif j == 0:arr[i][j] = arr[i - 1][j] + grid[i][j]else:arr[i][j] = min(arr[i][j - 1], arr[i - 1][j]) + grid[i][j]return arr[m - 1][n - 1]

class Solution:def minPathSum(self, grid: List[List[int]]) -> int:m, n = len(grid), len(grid[0])for i in range(m):for j in range(n):if i == 0 and j == 0:continueelif i == 0:grid[i][j] = grid[i][j - 1] + grid[i][j]elif j == 0:grid[i][j] = grid[i - 1][j] + grid[i][j]else:grid[i][j] = min(grid[i][j - 1], grid[i - 1][j]) + grid[i][j]return grid[-1][-1]

class Solution:def minPathSum(self, grid: List[List[int]]) -> int:m, n = len(grid), len(grid[0])arr = [[0] * n for _ in range(m)]for i in range(m):for j in range(n):if i == 0 and j == 0:arr[i][j] = grid[i][j]else:top = arr[i - 1][j] + grid[i][j] if i - 1 >= 0 else float('inf')left = arr[i][j - 1] + grid[i][j] if j - 1 >= 0 else float('inf')arr[i][j] = min(top, left)return arr[-1][-1]

2.5 第五炮：题目拓展-三角形最小路径和

LeetCode120
https://leetcode.cn/problems/triangle/description/

本题就是LeetCode64最小路径和的简单变换

思路分析

处理过程如下:
为了方便处理，我们可以先处理第1列和对角线

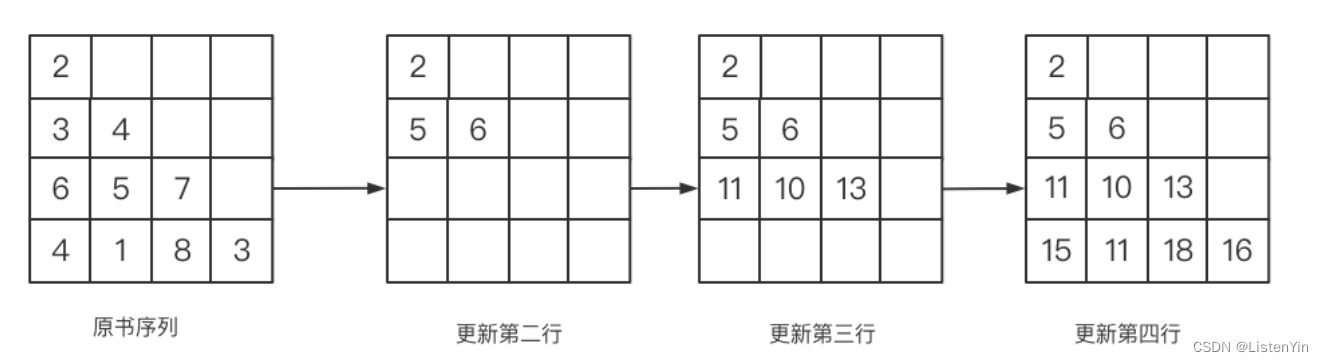
在这里插入图片描述

引入新概念 无后效性

无后效性：
我们转移某个状态需要用到某个值，但是并不关心该值是如何而来的
或者说，当前某个状态确定后，之后的状态转移与之前的决策无关

确定一道题目是否可以用 DP 解决，要从有无后效性进行分析。有后效性，不能用DP；无后效性，可以用DP。

本题中

  • 路径从上到小，最后一个点必然落在最后一行
  • 最后一行某个位置的值，只能从上一行的某一个位置或者某两个位置之一转移而来
  • 我们只关注前一位的累加值是多少，而不关心这个累加值结果是由什么路径而来，满足无后效性

找递推关系，确定状态

f[i][j] 代表到达某个点的最小路径和，min(f[n-1][i]) 就是答案，最后一行的每列的路径和的最小值

  • 第i行有i+1个数组（i从0开始）
  • 第一列位置上的数(j=0)，只能从 上方 转移而来
  • 最后一列位置上的数(j=i)，只能从 左上方 转移而来
  • 其他位置上的数(0<j<i)，可以从 上方 或者 左上方转移而来

代码实现

class Solution:def minimumTotal(self, triangle: List[List[int]]) -> int:m = len(triangle)n = len(triangle[-1])arr = [[0] * n for _ in range(m)]for i in range(m):for j in range(n):if j > i:continueelif j == 0:arr[i][j] = arr[i - 1][j] + triangle[i][j]elif j == i:arr[i][j] = arr[i - 1][j - 1] + triangle[i][j]else:arr[i][j] = min(arr[i - 1][j], arr[i - 1][j - 1]) + triangle[i][j]return min(arr[-1])if __name__ == '__main__':print(Solution().minimumTotal([[2], [3, 4], [6, 5, 7], [4, 1, 8, 3]]))  # 11

代码优化

class Solution:def minimumTotal(self, triangle: List[List[int]]) -> int:m = len(triangle)arr = [[0] * m for _ in range(m)]arr[0][0] = triangle[0][0]for i in range(1, m):arr[i][0] = arr[i - 1][0] + triangle[i][0]for j in range(1, i):arr[i][j] = min(arr[i - 1][j], arr[i - 1][j - 1]) + triangle[i][j]arr[i][i] = arr[i - 1][i - 1] + triangle[i][i]return min(arr[m - 1])

题目拓展

类似题目还有 LeetCode931 下降路径最小和 和 LeetCode1289 下降路径最小和II

3，. 理解动态规划

3.1 动态规划(DP)能解决哪类问题

  • 直观上，DP一般让找最值。例如最长公共子序列等。
  • 关键：DP问题的子问题不是相互独立的，如果递归直接分解会导致重复计算指数级增长。
  • DP最大的价值：消除冗余，加速计算

DP要满足 无后效性

  • 对于某个状态，可以只关注状态的值，而不需要关注状态是如何转移过来，可以考虑用 DP 解决

例如：
上面路径问题，从左上角走到右下角，两个问题：

  1. 求有多少种走法
  2. 输出所有的走法

分析：

  • 动态规划是无后效性的，只记录数量，不管怎么来的。A是DP问题，B不能用DP
  • 回溯可以记录所有的路径，B是个回溯的问题

回溯与DP的比较

回溯：能解决，但是解决效率不高
DP：计算效率高，但是不能找到满足要求的路径

如何区分：
DP只关心当前结果是什么，怎么来的就不管了，所以动态规划无法获得完整的路径
回溯能够获得一条甚至所有满足要求的完整路径

DP的基本思想：

  • 将待求解问题分解成若干个子问题，先求子问题，在从这些子问题中得到原问题的解。

注：既然要找“最”值，必然要做的就是穷举来找所有的可能，然后选择“最”的那个，这就是为什么在DP代码中大量判断逻辑都会被套上min()或者max()

既然穷举，那为啥还要有 DP 的概念？

  • 因为穷举过程中存在大量重复计算，效率低下，我们要使用记忆化搜索等方式来消除不必要的计算
  • 所谓记忆化搜索就是将已经计算好的结果先存在数组里，后面直接读就不再重复计算了

既然记忆化能解决问题，为啥DP这么难？

  • 因为DP问题一定具备“最优子结构”，这样才能让记忆时得到准确的结果
  • 什么是 最优子结构，还是要等后面具体问题再看

状态转移方程

  • 有了最优子结构之后，还要写出正确的状态转移方程，也就是递归关系，才能正确的穷举
  • 在DP里，大部分递推都可以通过数组实现，因此看起来代码结构一般是如下所示的for循环，这就是DP代码的基本模板

DP代码的基本模板

// 初始化base case，也就是初始化刚开始的几种场景，有几种枚举几种
dp[0][0][...] = base case// 进行状态转移
for 状态1 in 状态1的所有值for 状态2 in 状态2的所有值for ...dp[状态1][状态2][...] = 求最值max(选择1, 选择2, ...)

我们一般写状态规划只有一两层，不会太深，代码看起来特别简洁

动态规划的常见类型

常见类型比较多，从形式上看，有坐标型、序列型、划分型、区间型、背包型、博弈型等等
解题基本思路是一致的

一般来说，DP题目有以下三种基本的类型

  1. 计数相关
    有多少方式走到右下角，有多少种方式选出K个数使得***等
    不关心具体路径是什么

  2. 求最大最小值，最多最少等
    例如最大数字和、最长上升子序列长度、最长公共子序列、最长回文序列等

  3. 求存在性
    例如取石子游戏，先手是否必胜，能不能选出K个数使得***等

但是不管哪一种，解决问题的模板是类似的，都是：

  1. 第一步：确定状态和子问题，也就是枚举出某个位置所有的可能性
    对于DP，大部分题目分析最后一步更容易一些得到递推关系，同时将问题转换为子问题
  2. 第二步：确定状态转移方程，也就是数组要存储什么内容
    很多时候状态确定之后，状态转移方程也就确定了，我们可以将第一二部作为一个步骤
  3. 第三步：确定初始条件和边界情况
    注意细心，尽力考虑周全
  4. 第四步：按照从大到小的顺序计算：f[0] f[1] f[2]
    虽然我们计算是从f[0]开始，但是对于大部分DP问题，先分析最后一个往往更有利于寻找状态表达式
    因此我们后面的问题基本都是从右向左找递归，从左向右来计算

以上是我们分析DP问题的核心模板

总结

  • 我们要自始至终，都要在大脑里装一个数组 （可能是一维，或者二维）
  • 要看这个数组每个元素表示的含义是什么（状态）
  • 要看每个数组位置是根据谁来算（状态转移方程）
  • 然后就是从小到大挨着将数组填满（从小到大计算，实现记忆化搜索）
  • 最后看哪个位置是我们想要的结果（目的）

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.hqwc.cn/news/106978.html

如若内容造成侵权/违法违规/事实不符，请联系编程知识网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

人离自动断电设备的功能要求

人离自动断电设备的功能要求

人离开自动断电石家庄光大远通电气有限公司用电器待机能耗往往是一种不易被发现的“隐藏的浪费”&#xff0c; 如果将一户家庭的空调、洗衣机、电视、微波炉、电饭煲五类电器进行计算&#xff0c;待机功率在12W到15W&#xff0c;待机能耗0.2度到0.33度电。每年能耗73度到124.45…
阅读更多...
“交叉轮”轮融资后，哪吒汽车能否脚踏“风火轮”续写逆袭故事？

“交叉轮”轮融资后，哪吒汽车能否脚踏“风火轮”续写逆袭故事？

2023年的新能源汽车江湖&#xff0c;烟波浩渺的水面下暗潮汹涌。 从特斯拉年初打响降价第一枪&#xff0c;降价潮至今未见尾声。9月刚至&#xff0c;小鹏汽车、零跑汽车又推出了调价政策。 这一背景下&#xff0c;车企内卷加剧是必然。年初&#xff0c;哪吒汽车联合创始人、C…
阅读更多...
11.（Python数模）（预测模型三）多元线性回归预测

11.（Python数模）（预测模型三）多元线性回归预测

多元线性回归 简介 多元线性回归使用在自变量和因变量有逻辑相关性的情况中。在实际应用中&#xff0c;多元线性回归经常用于探索和解释变量之间的复杂关系&#xff0c;例如经济学、社会科学和自然科学等领域。它提供了一种统计工具来分析多个自变量对因变量的影响&#xff0…
阅读更多...
【运维 Pro】时序场景实践与原理 - 1. 分布与分区

【运维 Pro】时序场景实践与原理 - 1. 分布与分区

【运维 Pro】: 是由 YMatrix 售前和售后团队负责的栏目。除了介绍日常的数据库运维和使用知识&#xff0c;我们更希望能够通过介绍这些知识背后的原理&#xff0c;让大家和我们一起感知数据库的美妙。 摘要 有别于其它场景&#xff0c;时序场景中的数据、查询都有着更为明显的…
阅读更多...
python DVWA文件上传POC练习

python DVWA文件上传POC练习

首先&#xff0c;构造POC我们首先要明白漏洞利用的流程&#xff0c;然后要知道请求包的格式&#xff0c;然后才能针对性的POC 这里先选择低难度的文件上传&#xff0c;低难度的是没有任何过滤可以直接上传的&#xff0c;先上传一个php一句话木马&#xff0c;使用burpsuite抓包 …
阅读更多...
C语言——qsort()函数_学习笔记

C语言——qsort()函数_学习笔记

本文目录 一、qsort()介绍二、参数详解三、qsort()函数应用举例3.1 排序数组类型的数据3.2 排序结构体类型的数据 四、模拟实现qsort()函数4.1 冒泡排序简单介绍4.2 实现bubble_sort()函数 一、qsort()介绍 qsort()函数是一个库函数&#xff0c;包含在头文件 <stdliib.h>…
阅读更多...
实验课一 -- 粒子群算法PSO

实验课一 -- 粒子群算法PSO

文章目录 算法说明&#xff1a;算法流程&#xff1a;代码实现&#xff1a;结果展示&#xff1a;结束 算法说明&#xff1a; 我看了下别人写的&#xff0c;这个粒子群算法的思想来源与鸟类捕食 我按我的理解解释一下&#xff1a; 很多只鸟在草原找食物&#xff0c;所有鸟刚开始…
阅读更多...
如何使用bat脚本启动指定目录下的jar包

如何使用bat脚本启动指定目录下的jar包

士别三日&#xff0c;当刮目相待。——《三国志》 为了将一个java程序封装成一个简单易用的小工具&#xff0c;使用bat脚本启动jar包。 在txt文档中&#xff0c;键入&#xff1a; echo off java -jar %~dp0core\demo.jar 注意&#xff1a; 1、其中“core”是文件夹的名称&am…
阅读更多...
[学习笔记]DeepWalk图神经网络论文精读

[学习笔记]DeepWalk图神经网络论文精读

参考资料&#xff1a;DeepWalk【图神经网络论文精读】 word2vec 相关论文&#xff1a; Efficient Estimation of Word Representations in Vector Space Distributed Representations of Words and Phrases and their Compositionality 随机游走Ramdom Walk简述 通过随机游…
阅读更多...
软件设计模式(二)：工厂、门面、调停者和装饰器模式

软件设计模式(二)：工厂、门面、调停者和装饰器模式

前言 在这篇文章中&#xff0c;荔枝将会梳理软件设计模式中的四种&#xff1a;工厂模式、Facade模式、Mediator模式和装饰器Decorator模式。其中比较重要的就是工厂模式和装饰器模式&#xff0c;工厂模式在开发中使用的频数比较高。希望荔枝的这篇文章能讲清楚哈哈哈哈&#xf…
阅读更多...
【网络通信 -- WebRTC】FlexFec 基本知识点总结概述

【网络通信 -- WebRTC】FlexFec 基本知识点总结概述

【网络通信 -- WebRTC】FlexFec 基本知识点总结概述 【1】FlexFec 的保护方案 假设存在一组源数据包(D L)&#xff0c;其序列号从 1 开始运行到 D L 一维非交错行 FEC(1-D Non-interleaved Row FEC) : 一种连续的源数据包进行保护的方案&#xff0c;可用于恢复按行分组的源…
阅读更多...
配置远程访问：让外部网络用户能够使用公司内部的OA办公系统

配置远程访问：让外部网络用户能够使用公司内部的OA办公系统

文章目录 前言1. 确认在内网下能够使用IP端口号登录OA办公系统2. 安装cpolar内网穿透3. 创建隧道映射内网OA系统服务端口4. 实现外网访问公司内网OA系统总结 前言 现在大部分公司都会在公司内网搭建使用自己的办公管理系统&#xff0c;如OA、ERP、金蝶等&#xff0c;员工只需要…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023