个人学习记录，代码难免不尽人意。

今天又斥资买了今年春季的真题一试，呃，感觉尽力了，89分，在当年排名23，感觉还不错，没有出现读不懂的题目和没有思路的情况，扣的11分分别是第二题两个测试点超时（其实考试时已经有解决思路了，只是时间到了没有提交上，其中一个测试点超时我在考完试后五分钟解决了），还有最后一个大题有一个测试点错误。（这个我现在也想明白了，忘记判断必须是“心型”了，光是对称的不够，必须满足叶子节点的高度是先增再减再增再减的！当时忘了唉，不过题目给的数据到是挺集中，这个条件只有一个过不去）

A-1 The Winner over Squares and Primes
This is about a game of fighting all the squrare numbers and prime numbers.

At the very beginning, N people are sitting in N seats, and the seats are numbered from 1 to N, from left to right. Then for all the seats with their numbers being squares (such as 1, 4, 9, 16, …), those people sitting in must leave, and everyone else must shift toward left so that there is no empty seat between any of them. If there are more than one people left, the game continues, but instead of square numbers, this round will let everyone sitting in the prime seats leave, and then the rest of them will shift to fill the empty seats again.

The game continues with checking the square seats and prime seats alternatively, until there is only one winner left. You are supposed to tell the initial seat number for this winner.

Input Specification:
Each input file contains one test case, in which a positive integer N (≤10
5
) is given.

Output Specification:
For each test case, print in a line the initial seat number for this winner.

Sample Input:
10
Sample Output:
6
Hint:
Round 1: People sitting in square seats 1, 4, and 9 will leave. The initial seat numbers for the rest of them sitting from 1 to 7 are 2, 3, 5, 6, 7, 8, 10.

Round 2: People sitting in prime seats 2, 3, 5, and 7 will leave. The initial seat numbers for the rest of them sitting from 1 to 3 are 2, 6, 8.

Round 3: People sitting in square seat 1 will leave. The initial seat numbers for the rest of them sitting from 1 to 2 are 6, 8.

Round 4: People sitting in prime seat 2 will leave. The initial seat numbers for the final winner is 6.

#include<iostream>
#include<cstdio>
#include<vector>
#include<algorithm>
#include<cmath>
using namespace std;
vector<int> res,temp;
const int maxn=100100;//写成10010最后三个测试点过不去。
int hashtable[maxn]={0};
void getsquare(){int i=1;while(i*i<=maxn){hashtable[i*i]=1;i++;}
}
bool isprime(int n){if(n<=1) return false;int mid=(int)sqrt(1.0*n);for(int i=2;i<=mid;i++){if(n%i==0) return false;}return true;
}
int main(){int n;scanf("%d",&n);for(int i=1;i<=n;i++){res.push_back(i);}getsquare();while(res.size()>1){for(int i=0;i<res.size();i++){if(hashtable[i+1]!=1){temp.push_back(res[i]);}}res.clear();for(int i=0;i<temp.size();i++){if(!isprime(i+1)){res.push_back(temp[i]);}}temp.clear();}printf("%d\n",res[0]);} 

很简单的一道题，先求出平方数表然后判断即可。

A-2 LRU-K
Least Recently Used (LRU) cache scheme is to remove the least recently used frame (the one hasn’t been used for the longest amount of time) when the cache is full and a new page is referenced which is not there in cache.

LRU-K is a variant of the LRU algorithm, where K represents the number of recent uses. LRU can be considered as LRU-1. Unlike LRU, the LRU-K requires the maintenance of two different queues (for historical access and cache). The data in the historical access queue is not moved to the cache queue until the data is hit K times.

For example, assuming that the length of both queues is 5, and the memory is initialized to be empty. LRU-2 is used to process the data sequence in order: 9，5，6，7，8，3，8，9，5，9，8，3，4，7，5，6. The changes of the historical access queue and the cache queue are shown in the following table:

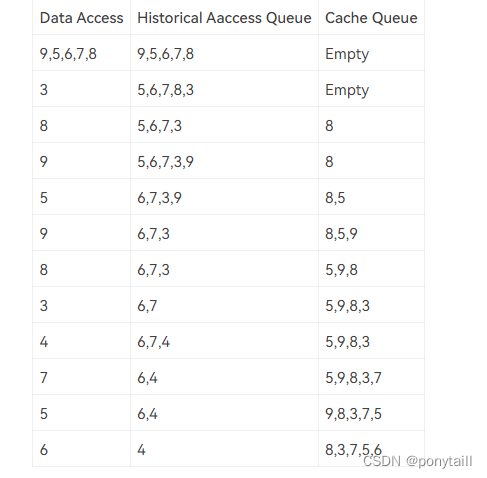
Your job is to implement this LRU-K cache scheme.

Input Specification:
Each input file contains one test case. For each case, the first line gives 3 positive integers: K (≤5), N (≤10 4 ) and M (≤10 5 ) which are the number of hits for cache, the size of the queues (assuming both queues have the same size) and the number of referenced page ID’s. Then M referenced page ID’s are given in the next line. A page ID is a number in the range [1,2×10 4 ]. All the numbers in a line are separated by a space.

Output Specification:
For each test case, output in the first line the page ID’s in the historical access queue, and in the second line, those in the cache queue. The ID’s are ordered from front to rear of each queue. All the numbers in a line must be separated by 1 space, and there must be no extra space at the beginning or the end of the line. In case that a queue is empty, output - in a line instead.

Sample Input 1:
2 5 17
9 5 6 7 8 3 8 9 5 9 8 3 4 7 5 6 9
Sample Output 1:
4 9
8 3 7 5 6
Sample Input 2:
3 5 10
9 5 6 7 8 3 8 9 5 9
Sample Output 2:
7 3 8 5 9

20分代码（应该是）

#include<iostream>
#include<cstdio>
#include<vector>
#include<algorithm>
#include<cmath>
#include<unordered_set>
#include<set>
using namespace std;
unordered_set<int> v1,v2;
const int maxn=100100;
int list[maxn];
int hashtable[maxn]={0};int main(){int k,n,m;scanf("%d %d %d",&k,&n,&m);for(int i=0;i<m;i++)
{scanf("%d",&list[i]);
}for(int i=0;i<m;i++){unordered_set<int>::iterator it2=v2.find(list[i]);if(it2!=v2.end()){v2.erase(it2);v2.insert(list[i]);}else{unordered_set<int>::iterator it1=v1.find(list[i]);if(it1==v1.end()){if(v1.size()<n){v1.insert(list[i]);}else{int cnt=v1.size();unordered_set<int>::iterator temp=v1.begin();for(int i=0;i<cnt-1;i++){temp++;}v1.erase(temp);v1.insert(list[i]);}}else{//hithashtable[list[i]]++;if(hashtable[list[i]]>=k-1){v1.erase(it1);if(v2.size()<n){v2.insert(list[i]);}else{int cnt=v2.size();unordered_set<int>::iterator temp=v2.begin();for(int i=0;i<cnt-1;i++){temp++;}v2.erase(temp);v2.insert(list[i]);}}else{v1.erase(it1); v1.insert(list[i]);}	}}//if(v1.empty()) printf("-\n");
//   else{
//   	int cnt=v1.size();
//   	for(unordered_set<int>::iterator it=v1.begin();it!=v1.end();it++){
//   	printf("%d",*it);
//   	cnt--;
//   	if(cnt>0) printf(" ");
//   	else printf("\n");
//   }
//   }
//   if(v2.empty()) printf("-");
//   else{
//   	int cnt=v2.size();
//   	for(unordered_set<int>::iterator it=v2.begin();it!=v2.end();it++){
//   	printf("%d",*it);
//   	cnt--;
//   	if(cnt>0) printf(" ");
//
//   }
//   }
//   printf("-----------------------------------------\n"); }vector<int> vec1,vec2; for(unordered_set<int>::reverse_iterator it=v1.rbegin();it!=v1.rend();it++){vec1.push_back(*it);}for(unordered_set<int>::iterator it=v2.begin();it!=v2.end();it++){
vec2.push_back(*it);}
if(v1.empty()) printf("-\n");
else{for(int i=vec1.size()-1;i>=0;i--){printf("%d",vec1[i]);if(i!=0)printf(" ");else printf("\n");}
}if(v2.empty()) printf("-");else{for(int i=vec2.size()-1;i>=0;i--){printf("%d",vec2[i]);if(i!=0)printf(" ");}}} 

这道题不是很难想，但是有两个测试点用vector来做一定会超时（涉及太多的删除和移动），因此我们遇到频繁删除和移动的题尽量用set或者map来做，在我改了之后代码应该可以过除了最后一个测试点以外的点。

A-3 K Vertex
Given a directed graph, a K-vertex is a vertex of which the out degree is larger than the indegree. For example, the vertices a and b in the figure are K-vertices.

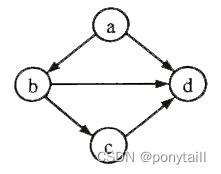
Your job is to list all the K-vertices in a given graph.

Input Specification:
Each input file contains one test case. For each case, the first line contains 2 positive integers: N (≤200) and M, which are the number of vertices and the number of edges, respectively. Then M lines follow, each gives a directed edge <v1, v2> in the format:

v1 v2
Here we assume that all the vertices are numbered from 0 to N−1. It is guaranteed that v1 is never the same as v2.

Finally a line of N strings is given, where the i-th string corresponds to the key of the i-th vertex (i=0,⋯,N−1). Each string consists of no more than 2 lower-cased English letters.

Output Specification:
Output the keys of all the K-vertices, each occupies a line, in alphabetical order. It is guaranteed that there is at least one output.

Sample Input:
4 5
0 1
2 1
3 1
2 0
3 2
c d b a
Sample Output:
a
b

#include<iostream>
#include<cstdio>
#include<vector>
#include<algorithm>
#include<cmath>using namespace std;
const int maxn=210;
const int INF=1000000000;
int G[maxn][maxn];
int indegree[maxn]={0};
int outdegree[maxn]={0};
vector<string> v;
int main(){for(int i=0;i<maxn;i++){for(int j=0;j<maxn;j++){G[i][j]=INF;}}int n,m;scanf("%d %d",&n,&m);for(int i=0;i<m;i++){int a,b;scanf("%d %d",&a,&b);G[a][b]=1;indegree[b]++;outdegree[a]++;}for(int i=0;i<n;i++){string str;cin >> str;if(outdegree[i]>indegree[i]){v.push_back(str);}}sort(v.begin(),v.end());for(int i=0;i<v.size();i++){cout << v[i];if(i!=v.size()-1) cout << endl;}
}       

有些简单了…

A-4 Tree of Love

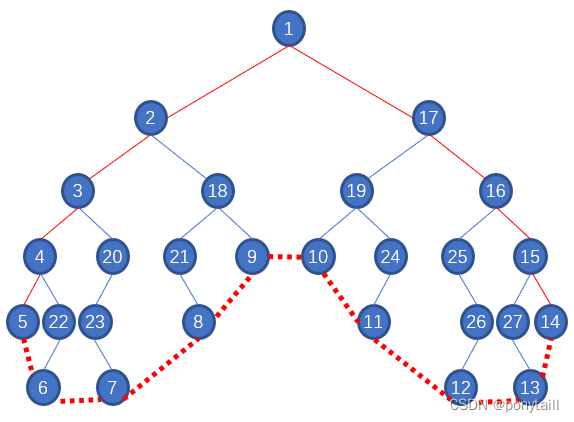
If a binary tree has its left and right subtrees perfectly symmetric. And more, if from left to right, the depths of leaves are first in increasing (or non-decreasing) then decreasing (or non-increasing), then again increasing (or non-decreasing), and finally decreasing (or non-increasing) order, then the shape of this tree looks like a heart (as shown by the above figure), and hence is called “Tree of Love”.

Given the inorder and postorder traversal sequences of a binary tree, your job is to construct this tree and test if it is a tree of love, and output its outer contour（外轮廓）. “Outer contour” consists of nodes visited from the root, along the left most path to a leaf, then all the leaves from left to right, and finally back to the root along the right most path.

Input Specification:
Each input file contains one test case. For each case, the first line gives a positive integer N (<100), which is the number of nodes in the tree. Then the next two lines each contains N positive keys as the inorder and postorder traversal sequences, respectively. All the keys are distinct integers no more than 10
3
. The numbers in a line are separated by spaces. It is guaranteed that a unique binary tree can be constructed from the input.

Output Specification:
For each test case, if the tree is a tree of love, output Yes in the first line, or No if not. Then output the outer contour in the second line.

All the numbers in a line must be separated by 1 space, and there must be no extra space at the beginning or the end of the line.

Sample Input 1:
27
5 4 6 22 3 23 7 20 2 21 8 18 9 1 10 19 11 24 17 25 12 26 16 27 13 15 14
5 6 22 4 7 23 20 3 8 21 9 18 2 10 11 24 19 12 26 25 13 27 14 15 16 17 1
Sample Output 1:
Yes
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
Sample Input 2:
11
4 8 10 2 5 1 6 3 9 11 7
10 8 4 5 2 6 11 9 7 3 1
Sample Output 2:
No
1 2 4 10 5 6 11 7 3
Hint for Sample 2:
The answer is No because the tree is not symmetric. It would be Yes if we swap 9 and 11 in the inorder sequence.

28分代码

#include<iostream>
#include<cstdio>
#include<vector>
#include<algorithm>
#include<cmath>
#include<queue>
using namespace std;
const int maxn=210;
int in[maxn];
int post[maxn];
vector<int> v;
struct node{int data;node* lchild;node* rchild;
};
node* newnode(int data){node* root=new node;root->data=data;root->lchild=NULL;root->rchild=NULL;return root; 
}
node* create(int postl,int postr,int inl,int inr){if(postl>postr) return NULL;int mid=post[postr];int index;for(int i=inl;i<=inr;i++){if(in[i]==mid){index=i;break;}}int leftnum=index-inl;node* root=newnode(mid);root->lchild=create(postl,postl+leftnum-1,inl,index-1);root->rchild=create(postl+leftnum,postr-1,index+1,inr);return root;
}
bool bfs(node* left,node* right){queue<node*> q1,q2;q1.push(left);q2.push(right);while(!q1.empty()&&!q2.empty()){node* lefttemp=q1.front();q1.pop();node* righttemp=q2.front();q2.pop();int tag1=0,tag2=0,tag3=0,tag4=0;if(lefttemp->lchild!=NULL){q1.push(lefttemp->lchild);tag1=1; }if(lefttemp->rchild!=NULL){q1.push(lefttemp->rchild);tag2=1; }//右子树应该先入右子树节点 if(righttemp->rchild!=NULL){q2.push(righttemp->rchild);tag3=1; }if(righttemp->lchild!=NULL){q2.push(righttemp->lchild);tag4=1; }if(tag1!=tag3||tag2!=tag4){
//			cout <<lefttemp->data<<endl;
//			cout << righttemp->data<<endl;
//			cout << tag1<<tag3<<tag2<<tag4<<endl; return false;}}if(!q1.empty()||!q2.empty()){return false;} else return true; 
}
void dfs(node* root){if(root==NULL) return;dfs(root->lchild);if(root->lchild==NULL&&root->rchild==NULL){v.push_back(root->data);}dfs(root->rchild);
}
void getleft(node* root){if(root==NULL) return;if(!(root->lchild==NULL&&root->rchild==NULL))v.push_back(root->data);getleft(root->lchild);
}
void getright(node* root){if(root==NULL) return;getright(root->rchild);if(!(root->lchild==NULL&&root->rchild==NULL))v.push_back(root->data);
}
int main(){int n;scanf("%d",&n);for(int i=0;i<n;i++){scanf("%d",&in[i]);}for(int i=0;i<n;i++){scanf("%d",&post[i]);}node* root=create(0,n-1,0,n-1);bool flag;if(root->lchild==NULL&&root->rchild==NULL){//测试点2需要特判数量为1 printf("Yes\n");printf("%d",root->data);return 0;}if(root->lchild==NULL&&root->rchild!=NULL||(root->rchild==NULL&&root->lchild!=NULL)){flag=false;}else flag=bfs(root->lchild,root->rchild);if(!flag){printf("No\n");}else printf("Yes\n");getleft(root);dfs(root);getright(root);v.pop_back();//右边多加了一个根节点 for(int i=0;i<v.size();i++){printf("%d",v[i]);if(i!=v.size()-1) printf(" ");}}   

这道题我忘记判断叶子节点的高度必须从左到右满足先增后减再增再减了，如果想要补上的话应该用bfs更新每个节点的高度，同时将所有叶子节点的高度存储在数组中，查看是不是先增后减再增再减（这个也好判断，设置信标即可），如果是再输出yes。