目录
题目:
示例:
分析:
代码:
题目:

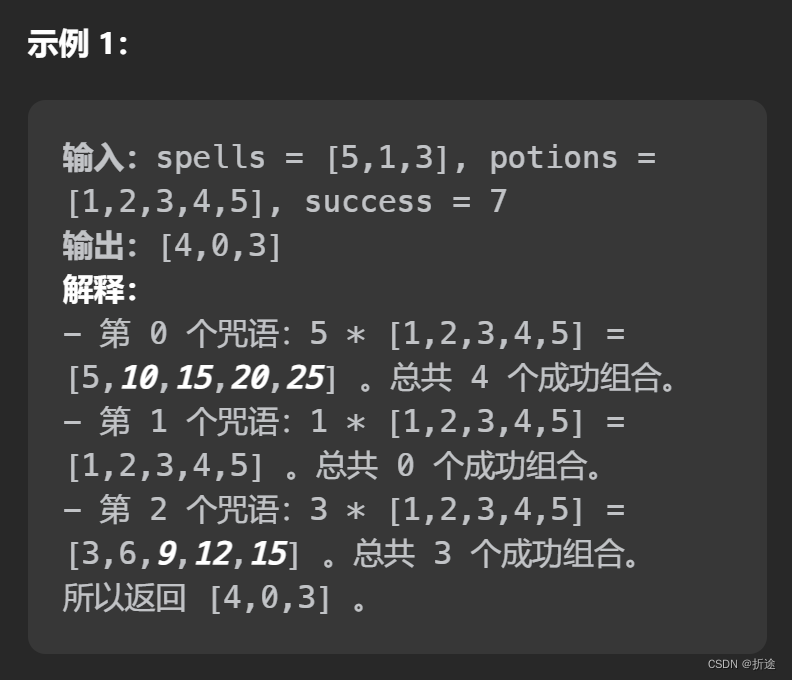
示例:
分析:
题目给我们两个数组,要我们找出第一个数组中每个元素能和另一个数组的元素匹配的数量。匹配的条件是乘积大于特定的值。
那么要乘积大于某个值,就需要乘数越大越好,我们可以把表示药水的数组升序排序,接着我们遍历咒语数组,再套一层for循环遍历药水数组,一旦我们发现乘积大于特定值了,那么结束遍历,因为后面的药水都比当前的药水的值要更大,乘积也就只会更大,也就是会大于特定值,所以该咒语能匹配的药水数量就是药水数组的长度减去当前遍历到的药水下标值。
这么做会超时,那么我们需要进一步优化代码,既然是乘积,那么是有两个乘数,我们只对其中一个乘数进行了排序,那么我们把另一个乘数,也就是咒语数组也进行排序,那么就可以再次减少不必要的重复遍历。
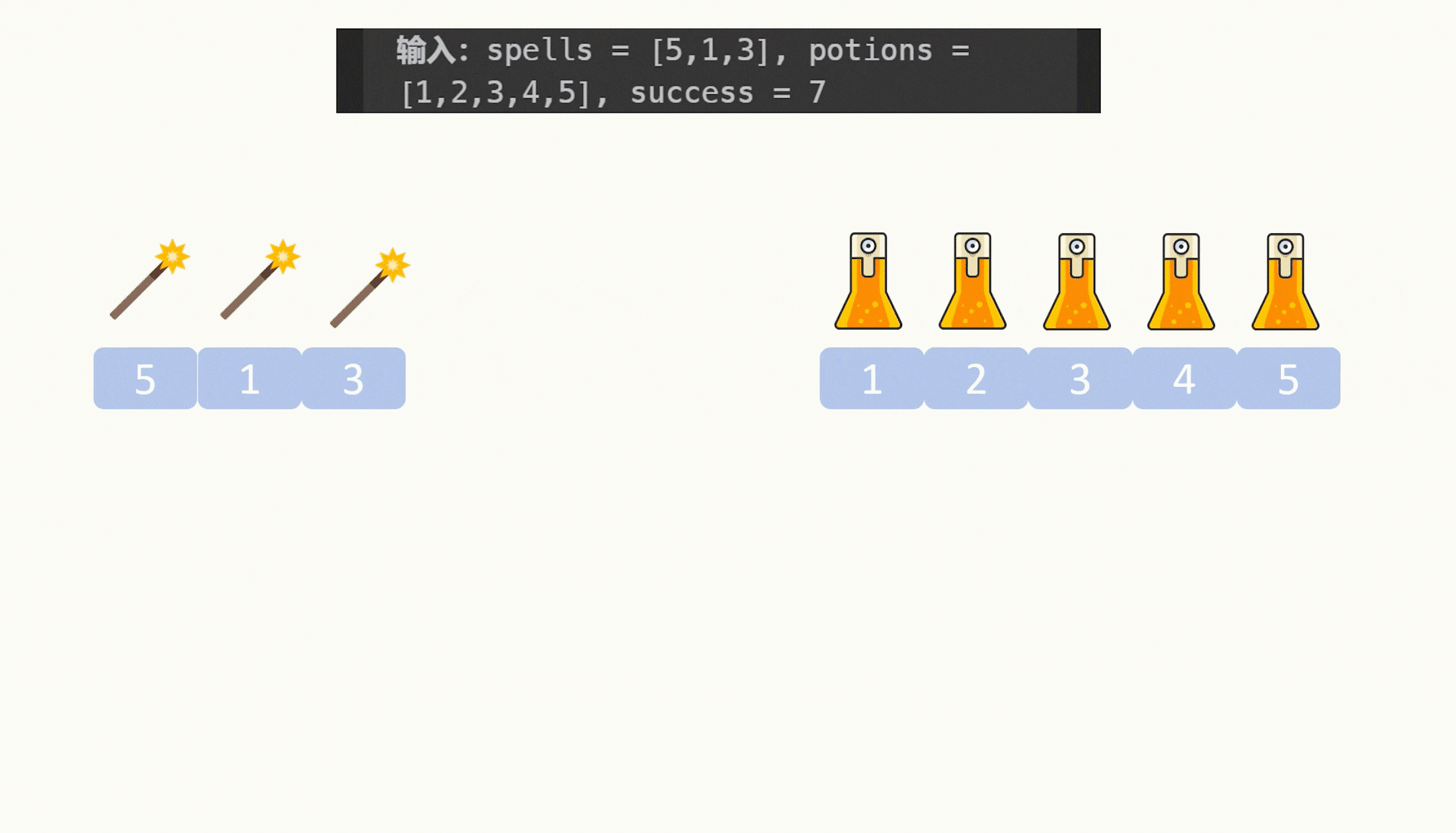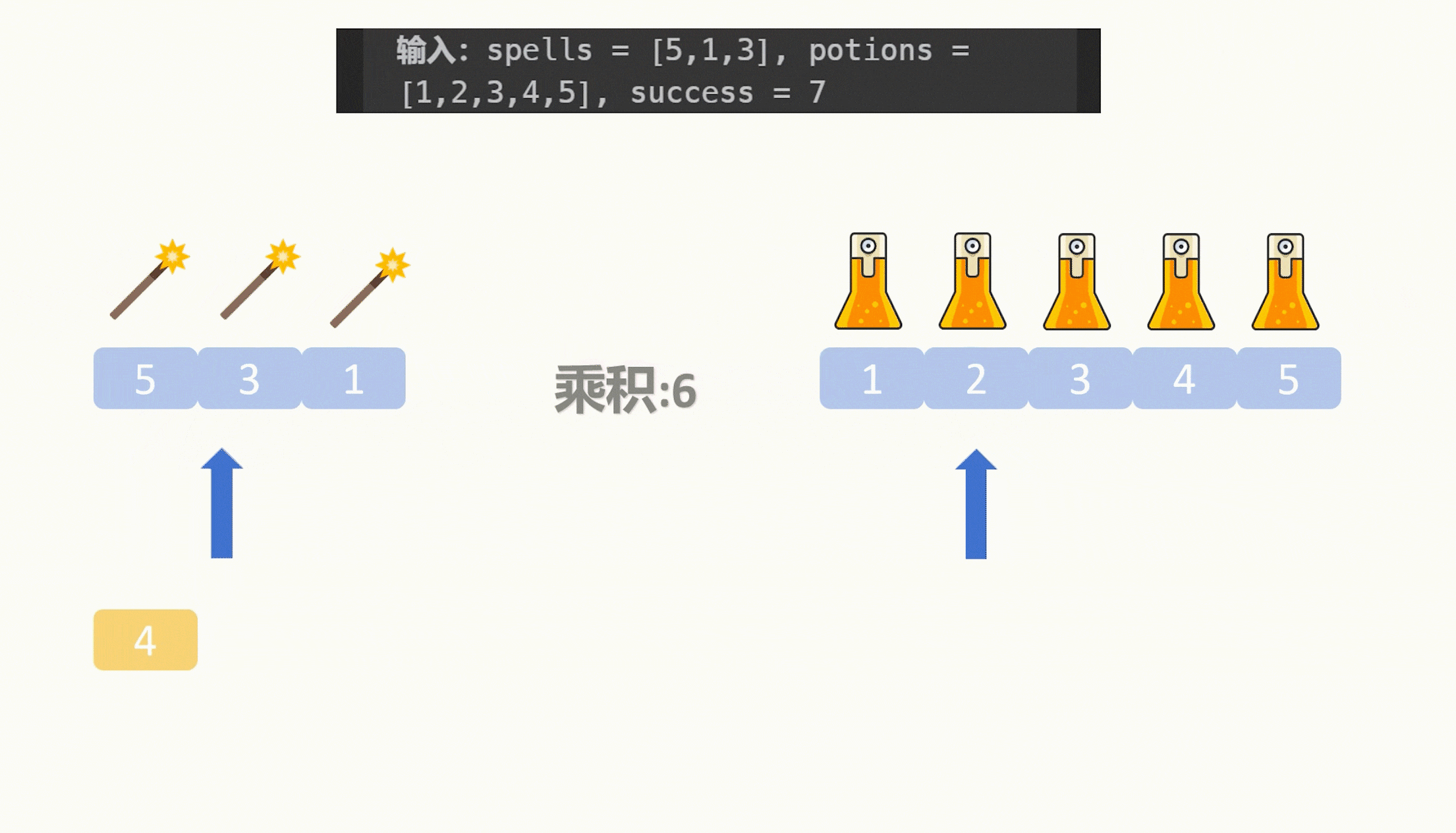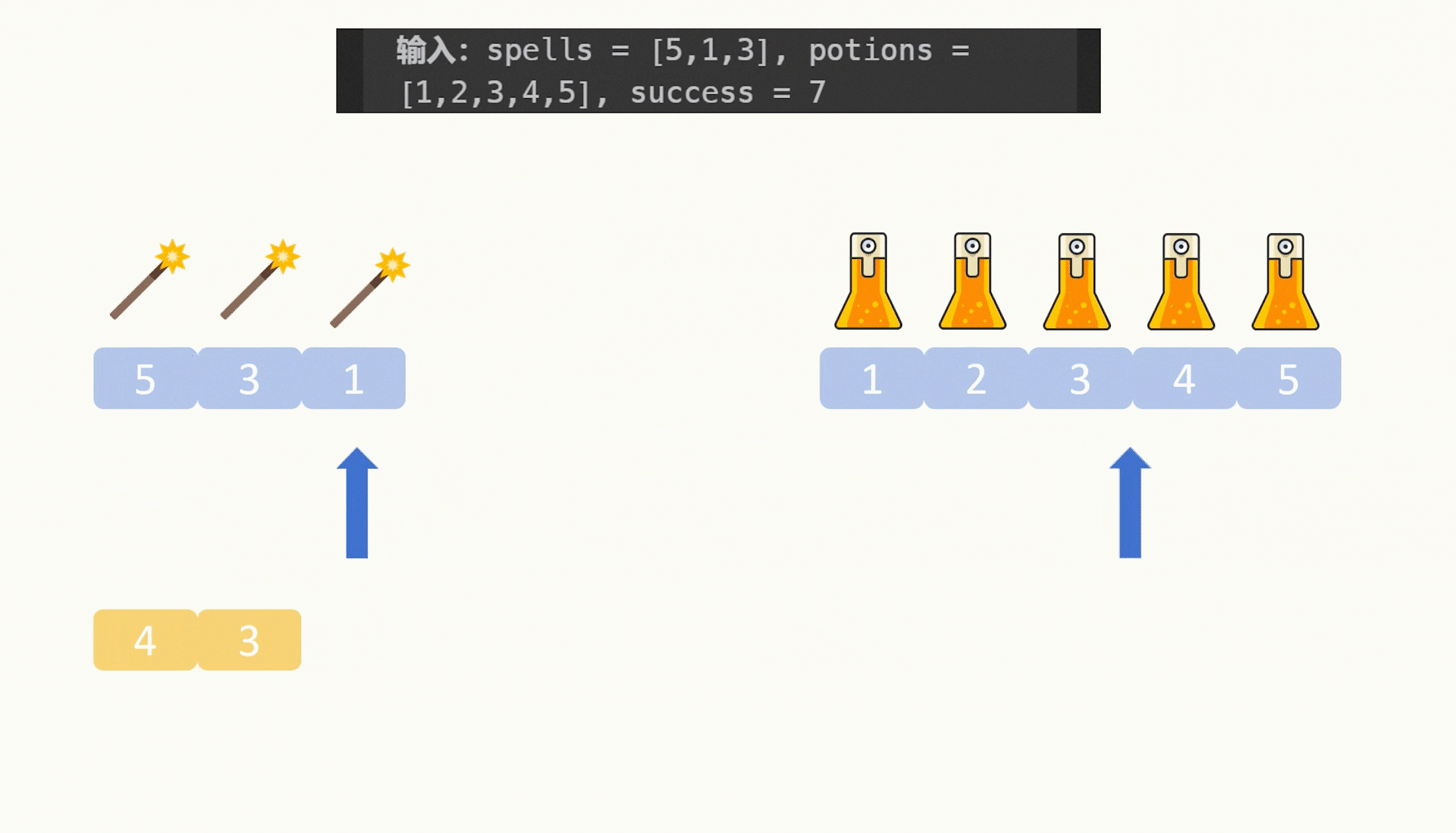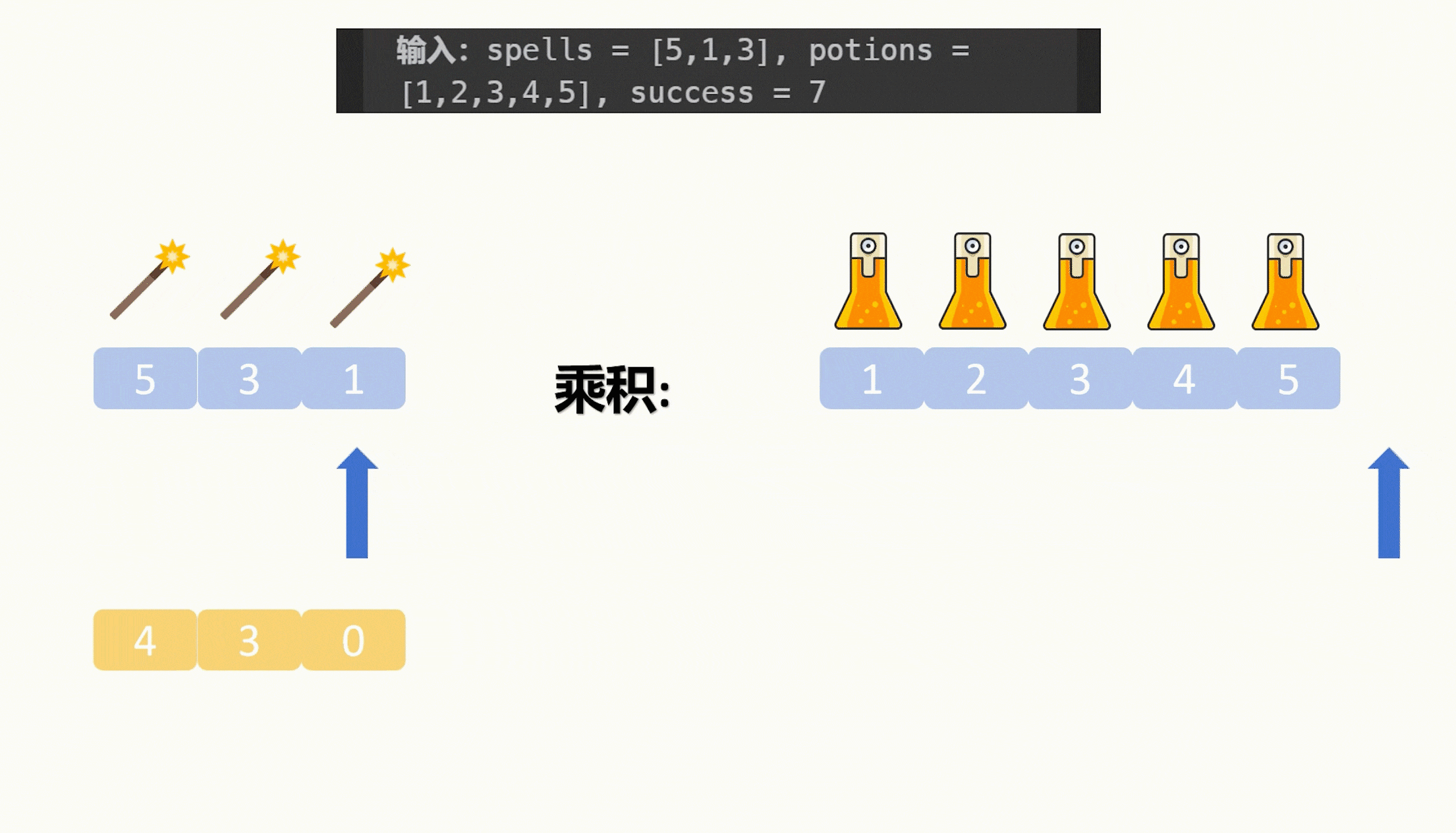
我们把咒语降序排序,然后再遍历咒语,在遍历咒语的时候拿一个指针来遍历升序的药水数组,如果当前咒语和药水的乘积大于特定值了,那么该咒语能匹配的药水数量就是药水数组的长度减去当前遍历到的药水下标值,这个和刚才的没有什么区别,区别在于我们用一个指针保存了药水的遍历情况,轮到下一个咒语时,我们接着刚才的药水位置接着遍历直到乘积再次大于特定值即可。
由于咒语按照从大到小的顺序排序,咒语是越来越小的,要保持乘积大于特定值,那么接着从上一个较大的咒语能第一个匹配到的药水下标开始接着寻找更大的能匹配本次咒语的药水下标即可,而不需要像第一次那样从头开始寻找。
由于答案是和初始咒语数组的下标匹配的,所以我们不能直接对咒语数组进行排序,我们可以拿一个数组来存放下标,对这个存放下标的数组按照咒语数组的值来进行排序,这样存放下标的数组排完序后,元素映射到咒语数组就是排序好的咒语数组了,接着我们用遍历这个下标数组来代替咒语数组即可。
代码:
class Solution {
public:vector<int> successfulPairs(vector<int>& spells, vector<int>& potions, long long success) {int n=spells.size();vector<int>temp(n); //存放spells的索引for(int i=0;i<n;i++) temp[i]=i;sort(temp.begin(),temp.end(),[&](int a,int b){ //将spells的索引按照从小到大排序return spells[a]<spells[b];});sort(potions.begin(),potions.end(),[](int a,int b){return a>b;});//将potions按照从大到小的顺序排序.vector<int>res(n);int index=0; //存放强度大于success的数目(potions的索引)for(int i=0;i<n;i++){if(index==n) res[temp[i]]=index-1;while(index<potions.size() && success<=static_cast<long long>(spells[temp[i]])*static_cast<long long>(potions[index])){ //由于spells按照从小到大的顺序,而potions按照从大到小的顺序排序,如果较小的spell乘potion能大于success,那么更大的spell也可以,因此不用从0开始遍历,直接存放在index中.index++;}res[temp[i]]=index;}return res;}
};