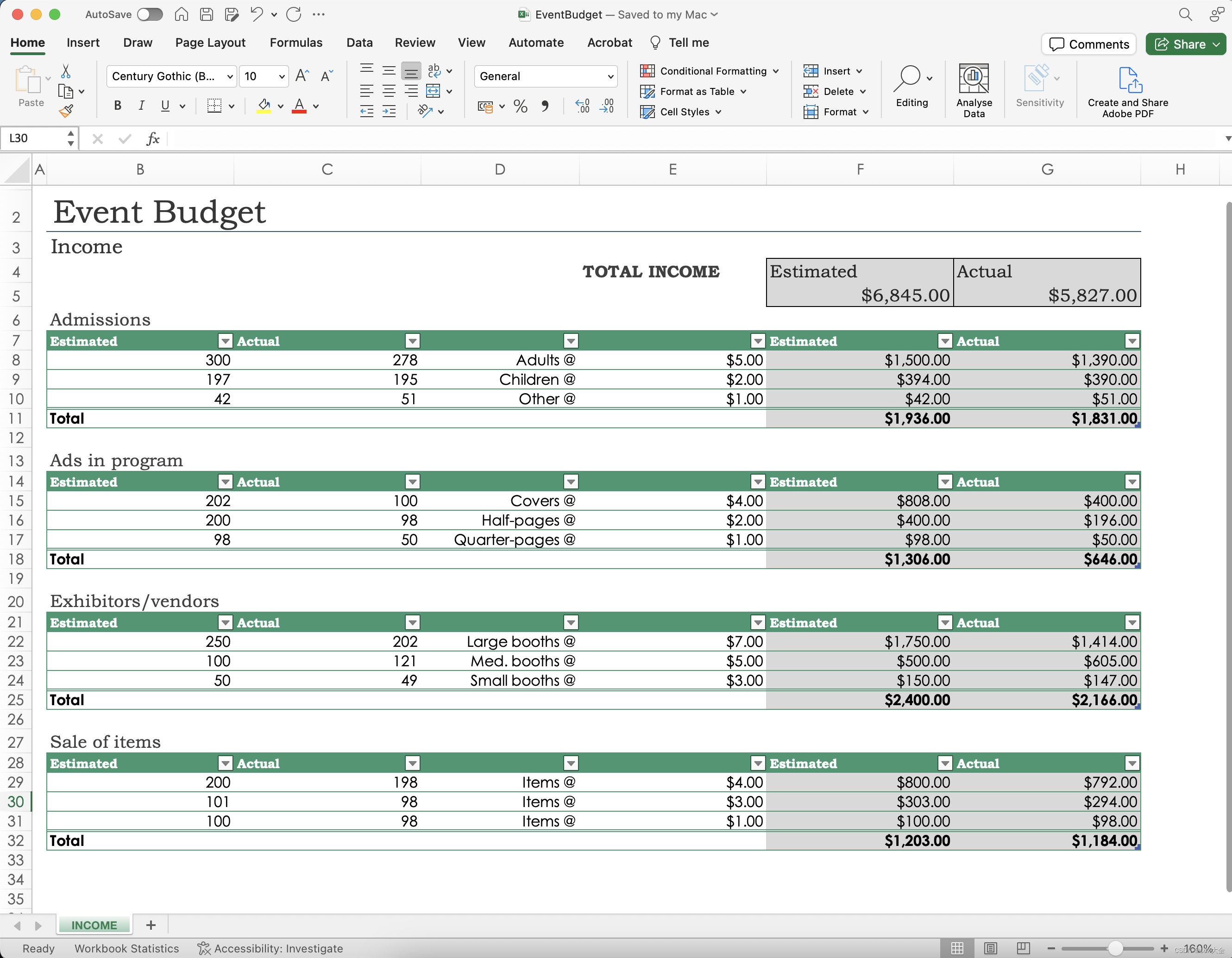
WebGL透视投影_山楂树の的博客-CSDN博客中的PerspectiveView代码一个问题是,我们用了一大段枯燥的代码来定义所有顶点和颜色的数据。示例中只有6个三角形,我们还可以手动管理这些数据,但是如果三角形的数量进一步增加的话,那可真就是一团糟了。幸运的是,对这个问题,确实还有更高效的方法。
仔细观察下图,你会发现左右两组三角形的大小、位置、颜色都是对应的。如果在虚线标识处也有这样3个三角形,那么将它们向X轴正方向平移0.75单位就可以得到右侧的三角形,向X轴负方向平移0.75单位就可以得到左侧的三角形。
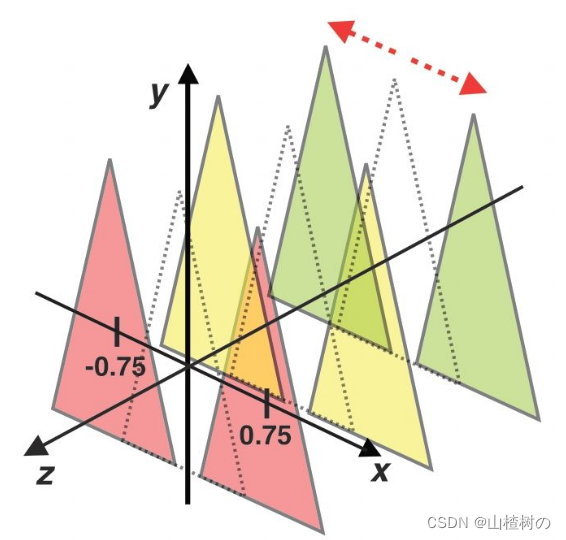
利用这一点,我们只需按照下面的步骤,就能获得WebGL透视投影_山楂树の的博客-CSDN博客的效果了:
1.在虚线处,即沿着Z轴准备3个三角形的顶点数据。
2.将其沿X轴正方向(以原始位置为基准)平移0.75单位,绘制这些三角形。
3.将其沿X轴负方向(以原始位置为基准)平移0.75单位,绘制这些三角形。
示例程序PerspectiveView_mvp就尝试这样做。
PerspectiveView程序使用投影矩阵定义可视空间,使用视图矩阵定义观察者,而PerspectiveView_mvp程序又加入了模型矩阵,用来对三角形进行变换。
矩阵推导
我们有必要复习一下矩阵变换。请看之前编写的WebGL 视图矩阵、模型视图矩阵_山楂树の的博客-CSDN博客程序LookAtRotatedTriangles,该程序允许观察者从自定义的位置观察旋转后的三角形。等式1描述了三角形顶点的变换过程。
<视图矩阵>×<模型矩阵>×<顶点坐标>
后来的LookAtTriangles_ViewVolume程序(该程序修复了三角形的一个角被切掉的错误)使用等式2来计算最终的顶点坐标,其中投影矩阵有可能是正射投影矩阵或透视投影矩阵。
<投影矩阵>×<视图矩阵>×<顶点坐标>
可以从上述两式推断出等式3:
<投影矩阵>×<视图矩阵>×<模型矩阵>×<顶点坐标>
等式3表示,在WebGL中,你可以使用投影矩阵、视图矩阵、模型矩阵这3种矩阵计算出最终的顶点坐标(即顶点在规范立方体中的坐标)。
如果投影矩阵为单位阵,那么等式3与等式1就完全相同了;同样,如果模型矩阵为单位阵,那么等式3与等式2就完全相同了。单位阵就像乘法中的1一样,它乘以任意一个矩阵,或者任意一个矩阵乘以它,得到的结果还是这个矩阵(程序中不设置投影矩阵所需的任一参数,默认参数所计算得到的矩阵可理解为1)。
模型视图投影矩阵示例代码(PerspectiveView_mvp)
var VSHADER_SOURCE ='attribute vec4 a_Position;\n' +'attribute vec4 a_Color;\n' +'uniform mat4 u_ModelMatrix;\n' +'uniform mat4 u_ViewMatrix;\n' +'uniform mat4 u_ProjMatrix;\n' +'varying vec4 v_Color;\n' +'void main() {\n' +' gl_Position = u_ProjMatrix * u_ViewMatrix * u_ModelMatrix * a_Position;\n' +' v_Color = a_Color;\n' +'}\n';var FSHADER_SOURCE ='#ifdef GL_ES\n' +'precision mediump float;\n' +'#endif\n' +'varying vec4 v_Color;\n' +'void main() {\n' +' gl_FragColor = v_Color;\n' +'}\n';function main() {var canvas = document.getElementById('webgl');var gl = getWebGLContext(canvas);if (!initShaders(gl, VSHADER_SOURCE, FSHADER_SOURCE)) return// 设置顶点坐标和颜色(蓝色三角形在前面)var n = initVertexBuffers(gl);gl.clearColor(0, 0, 0, 1);// 获取u_ModelMatrix、u_ViewMatrix和u_ProjectMatrix的存储位置var u_ModelMatrix = gl.getUniformLocation(gl.program, 'u_ModelMatrix');var u_ViewMatrix = gl.getUniformLocation(gl.program, 'u_ViewMatrix');var u_ProjMatrix = gl.getUniformLocation(gl.program, 'u_ProjMatrix');var modelMatrix = new Matrix4(); // 模型矩阵var viewMatrix = new Matrix4(); // 视图矩阵var projMatrix = new Matrix4(); // 投影矩阵// 计算视图矩阵和投影矩阵modelMatrix.setTranslate(0.75, 0, 0); // 沿正x轴平移0.75个单位viewMatrix.setLookAt(0, 0, 5, 0, 0, -100, 0, 1, 0); // 视点、观察点、正方向projMatrix.setPerspective(30, canvas.width/canvas.height, 1, 100); // 视角、近截面宽高比、near、far// 将模型、视图和投影矩阵分别传递给统一变量gl.uniformMatrix4fv(u_ModelMatrix, false, modelMatrix.elements);gl.uniformMatrix4fv(u_ViewMatrix, false, viewMatrix.elements);gl.uniformMatrix4fv(u_ProjMatrix, false, projMatrix.elements);gl.clear(gl.COLOR_BUFFER_BIT); gl.drawArrays(gl.TRIANGLES, 0, n); // 绘制右侧三角形// 为另一对三角形准备模型矩阵modelMatrix.setTranslate(-0.75, 0, 0); // 沿负x轴平移0.75个单位// 仅修改模型矩阵gl.uniformMatrix4fv(u_ModelMatrix, false, modelMatrix.elements);gl.drawArrays(gl.TRIANGLES, 0, n); // 绘制左侧三角形
}function initVertexBuffers(gl) {var verticesColors = new Float32Array([// 顶点坐标和颜色0.0, 1.0, -4.0, 0.4, 1.0, 0.4, // 后面的绿色-0.5, -1.0, -4.0, 0.4, 1.0, 0.4,0.5, -1.0, -4.0, 1.0, 0.4, 0.4, 0.0, 1.0, -2.0, 1.0, 1.0, 0.4, // 中间的黄色-0.5, -1.0, -2.0, 1.0, 1.0, 0.4,0.5, -1.0, -2.0, 1.0, 0.4, 0.4, 0.0, 1.0, 0.0, 0.4, 0.4, 1.0, // 前面的蓝色-0.5, -1.0, 0.0, 0.4, 0.4, 1.0,0.5, -1.0, 0.0, 1.0, 0.4, 0.4, ]);var n = 9;var vertexColorbuffer = gl.createBuffer(); gl.bindBuffer(gl.ARRAY_BUFFER, vertexColorbuffer);gl.bufferData(gl.ARRAY_BUFFER, verticesColors, gl.STATIC_DRAW);var FSIZE = verticesColors.BYTES_PER_ELEMENT;var a_Position = gl.getAttribLocation(gl.program, 'a_Position');gl.vertexAttribPointer(a_Position, 3, gl.FLOAT, false, FSIZE * 6, 0);gl.enableVertexAttribArray(a_Position);var a_Color = gl.getAttribLocation(gl.program, 'a_Color');gl.vertexAttribPointer(a_Color, 3, gl.FLOAT, false, FSIZE * 6, FSIZE * 3);gl.enableVertexAttribArray(a_Color);return n;
}
代码详解
顶点着色器第9行实现了等式3
![]()
main()函数调用initVertexBuffers()函数(第27行),定义将要传给缓冲区对象的三角形顶点数据(第58行)。我们只定义了3个三角形,其中心都在Z轴上。而在PerspectiveView.js中,我们在Z轴两侧共定义了6个三角形。前面说过,这是因为这3个三角形将与平移变换结合使用。
接着,我们获取了顶点着色器中u_ModelMatrix变量的存储地址(第30行),然后新建了模型矩阵modelMatrix对象(第34行),并根据参数将其计算出来(第39行)。此时,该模型矩阵会将三角形向X轴正方向平移0.75单位。
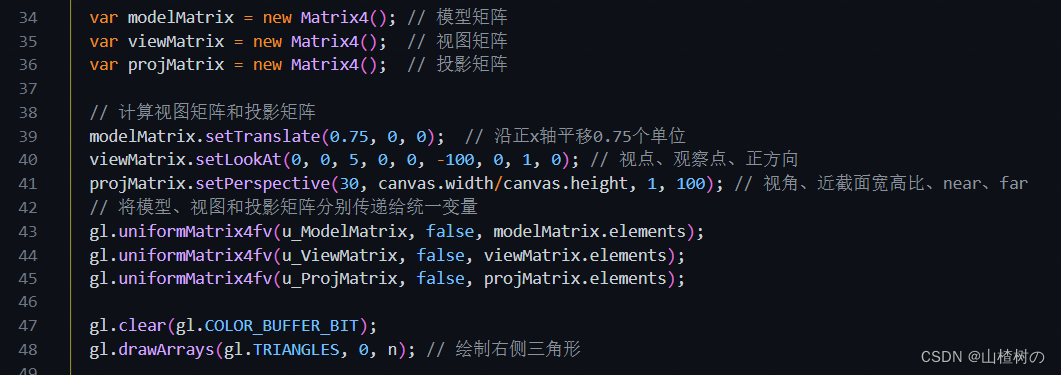
除了计算模型矩阵(第39行),计算视图矩阵和投影矩阵的过程与PerspectiveView.js中一样。模型矩阵被传给u_ModelMatrix(第43行)并进行绘制,绘制了Z轴右侧的3个三角形(第48行)。
下面以相似的方式来绘制左侧的三角形:首先重新计算模型矩阵(第51行),使之将初始的三角形沿X轴负方向平移0.75单位。算出新的模型矩阵后,传给着色器,再调用gl.drawArrays()进行绘制,就画出了左侧的三角形。视图矩阵和投影矩阵不需要变化,不需要管它们。

如你所见,程序只使用了一套数据(3个三角形的顶点和颜色信息)就画出了两套图形(6个三角形)。这样做虽然减少了顶点的个数,但是增加了调用gl.drawArrays()的次数。哪一种方法更高效,或者如何在这两者之间平衡,依赖于程序本身和WebGL的实现。