文章目录
- 前言
- 一、散列表的基本概念
- 二、散列函数的构造方法
- 三、处理冲突的方法
- 1. 开放定址法:
- 2. 拉链法
- 四、散列查找及性能分析
- 总结
前言
- 散列表的基本概念
- 散列函数的构造方法
- 处理冲突的方法
- 散列查找及性能分析
提示:以下是本篇文章正文内容,下面案例可供参考
一、散列表的基本概念
- 概念:之前的算法建立在“比较”基础上,效率取决于比较次数
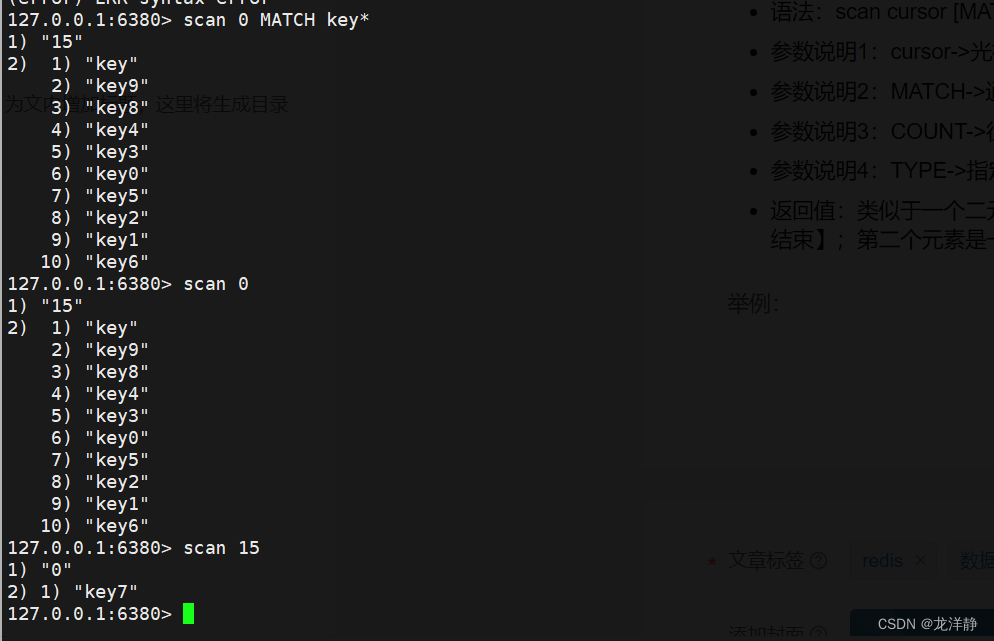
散列函数:将关键字映射成该关键字对应地址的函数,记为Hash(key)=Addr,散列函数会把两个不同的关键字映射到同一地址,称为“冲突”,发生碰撞的不同关键字称为同义词;应尽量减少冲突,设计好的处理冲突的方法 - 哈希表:一个有限的连续的地址空间,用以容纳按哈希地址存储的记录。
- 哈希函数:记录的存储位置与它的关键字之间存在的一种对应关系。 Loc(ri)=H(keyi)。
- 同义词:在同一地址出现冲突的各关键字。
- 哈希(散列)地址:根据设定的哈希函数H(key)和处理冲突的方法确定的记录的存储位置。
- 装填因子:表中填入的记录数n和哈希表表长 m之比。
- α=n/m
二、散列函数的构造方法
- 函数定义域必须包括全部需要存储的关键字
- 散列函数计算出的地址能够等概率、均匀分布在整个地址空间,减少冲突
- 散列函数尽量简单,较短时间内能计算出任意关键字的地址
- 直接定址法:散列函数为 ;不会产生冲突,适合关键字分布基本连续的情况,若分布不连续,则空位较多,造成空间浪费
- 除留余数法:假定表长为m,取一个不大于m但最接近或等于m的质数p,散列函数为H(key)=key%p(需要选取好p)
- 开放定址法 (空缺编址法)
Hi = ( H(key)+ di ) MOD m
i=1,2, …, k (km-1)
m:哈希表的表长; di:增量序列
1)线性探测再散列 di= 1,2, …, m-1
缺陷:有聚集(堆积)现象—非同义词地址冲突。
2)二次探测再散列
di= 12, -12, 22, -22, 32,…,k2 k m/2
缺陷:不易探查到整个散列空间。
3)伪随机探测再散列 di = 伪随机数序列
链地址法
为每个哈希地址建立一个单链表,存储所有具有同义词的记录。
冲突处理简单,无堆积现象,平均查找长度较短;
较适合于事先无法确定表长的情况;
可取α≥1,当结点信息规模较大时,节省空间
删除结点的操作易于实现
[设计哈希表的过程]
1)明确哈希表的地址空间范围。即确定哈希函数的值域。
2)选择合理的哈希函数。该函数要保证所有可能的记录的哈希地址均在指定的值域内,并使冲突的可能性尽量小。
3)设定处理冲突的方法。
三、处理冲突的方法
为产生冲突的关键字寻找下一个“空”的Hash地址,用Hi表示冲突后第i次探索的散列地址
1. 开放定址法:
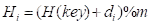
,m表示表长,di表示增量
(1)线性探索法:di=1开始,每次递增1,向后查找空位,直到找到一个空位或查遍全表;缺点:可能使第i个散列地址同义词存在第i+1个,造成大量相邻的散列地址聚集,大大降低了查找效率
(2)平方探测法: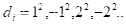
,k<=m/2 ,m=4k+3,又称二次探测法;可以避免堆积问题,缺点是不能探测到表的全部单元,但至少可以探测到一半
(3)再散列法:使用两个散列函数进行散列
注意:不能随便删除表中元素,因为若删除元素将会截断其他具有相同散列地址的元素的查找地址,所以要想删除一个元素,给它做一个标记,进行逻辑删除,但副作用是表面上看起来散列表很满,实际上有许多位置没有利用
2. 拉链法
(1)为避免非同义词发生冲突,可以把所有同义词存储在一个线性链表中,这个线性链表由散列地址唯一标识,拉链法适用于经常进行插入和删除的情况
四、散列查找及性能分析
1.散列查找
(1)初始化:根据散列函数计算出散列地址,addr=Hash(key)
(2)检测表中addr位置上是否有记录,没有记录则失败;若有记录比较它与key值,若相等返回成功标志,不然执行下面(3)
(3)用给定的处理冲突的方法计算“下一散列地址”,并把addr置为此地址,转入(2)

2.散列查找效率:取决于散列函数、处理冲突方法和装填因子
3.装填因子: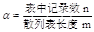
平均查找长度依赖于装填因子; 越大,装填记录越满,冲突可能性越大,散列表查找成功与 有关,与表长无关
例题:
例1:已知一组关键字为(26,36,41,38,44,15,68,12,06,51,25),用线性探查法解决冲突构造这组关键字的哈希表。表长取15,哈希函数H(key)=key MOD 13。并求出等概率情况下查找成功的平均查找长度ASL.

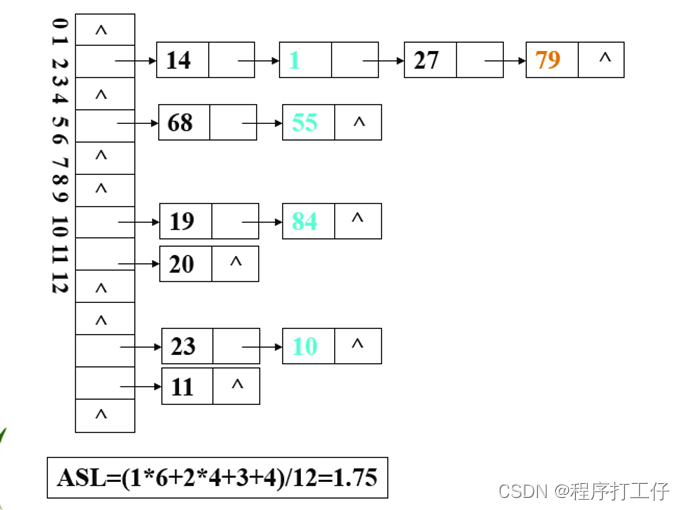
例2:已知一组关键字(19,14,23,1,68,20,84,27,55,11,10,79),哈希函数为:H(key)=key MOD 13, 哈希表长为m=16,设每个记录的查找概率相等
总结
- 散列表的基本概念
- 散列函数的构造方法
- 处理冲突的方法
- 散列查找及性能分析