supervised learning

• 贝叶斯估计

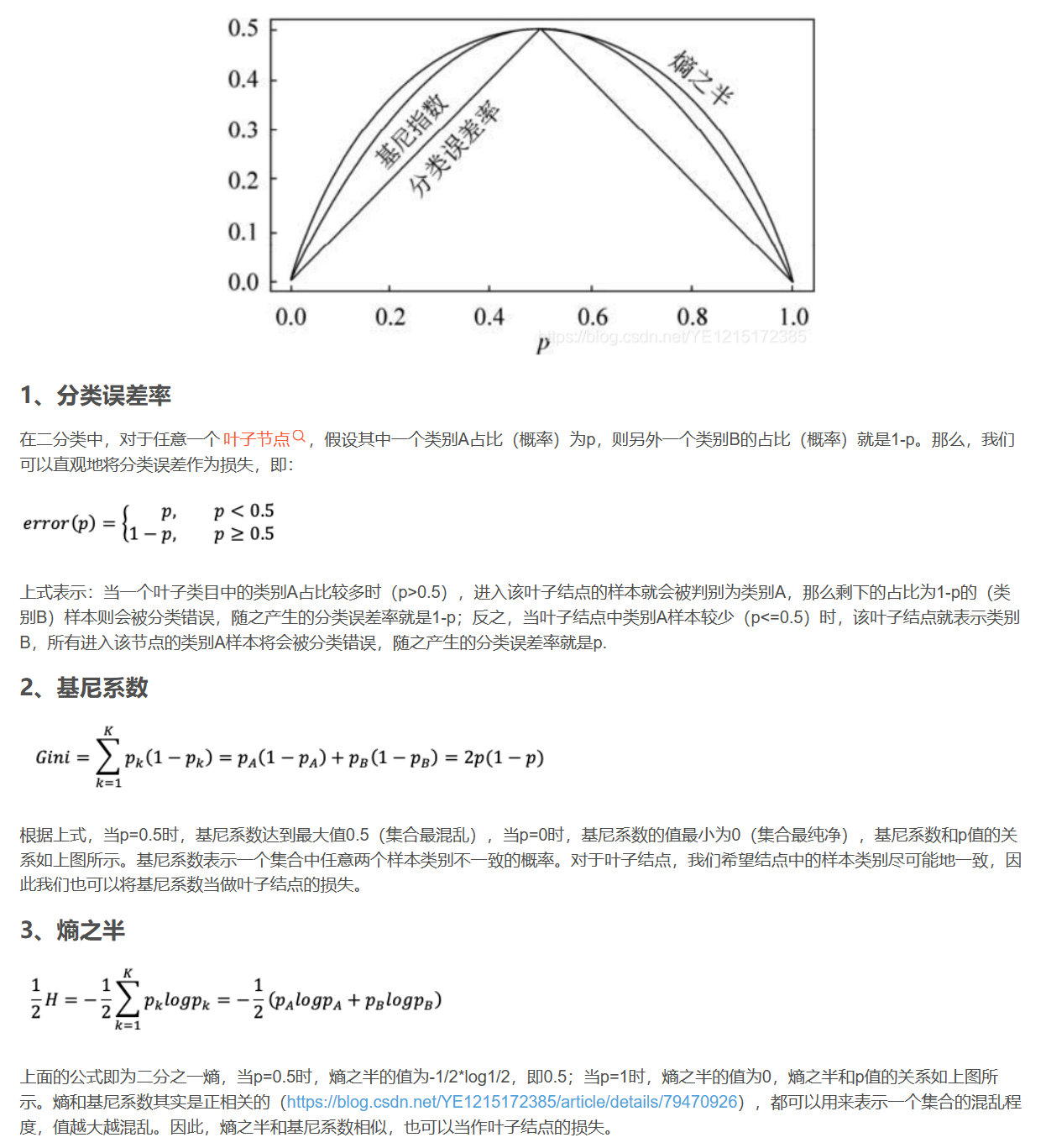
• 决策树与信息熵

  • 信息熵$H(D)=-{\sum }_{i=1}^{n}p(X=x_i)log(P(X=x_i))=-\sum p_{i}log(p_i)$，信息熵越大，(种类的)不确定度越大，H(D)=0，样本完全确定
  • 对分类问题，按照信息熵$\to$信息增益比=$\frac{1}{H_A(D)}g(D,A)=\frac{1}{H_A(D)}(H(D)-H(D,A))$最大化的原则选择特征，逐级下降形成决策树,
  • 据信息熵的有ID3，C4.5 alg
  • ifC(Tson)>C(Tpat)，cut Tson，有CART算法，对regression question，select j,s to minimize ${\sum }_{x\in R_1(j,s)}(y_i-c_1{)}^2+{\sum }_{x\in R_2(j,s)}(y_2-c_2{)}^2$
  • to sorting problem,based on $Gin{i}_A(D)$(similar to information entropy)，select A to minimize Gini(D)，剪枝，select best tree
  • 

• logistic

  • logistic采用极大似然估计，和最大熵模型$-\sum \tilde{P}(x)P(y|x)logP(y|x)$(其中P(y|x)满足$E_P(f_i)=E_{\tilde{P}}(f_i)$),求$\underset{P\in C}{\min }\underset{w}{\max }L(P,w)$
  • 对偶问题，$\underset{w}{\max }\underset{P\in C}{\min }L(P,w)$
  • 对$\underset{P\in C}{\min }L(P,w)$ ，对P(y|x)求导，转化为求$\underset{w}{\max }\psi (w)$，
  • 这一步用improved iterative scaling求$L(w)=\sum _{x,y}\tilde{P}(x,y){\sum }_{i=1}^n{w}_i{f}_i(x,y)-\sum _x\tilde{P}(x)log{Z}_w(x)$关于w的极大值，或用拟牛顿法

• SVM

  • 硬间隔支持向量机、软间隔支持向量机、非线性支持向量机（核方法）

• Boost方法——组合权重不同的同一种分类器，得到强分类器

1. Boost与前向分布算法的联系

2. 二分类学习，boost 错误分类的sample weight和误差率低的分类器权重，可用加法模型、损失函数为指数函数、的前向学习算法解释

3. 回归学习提升树，
   利用前向分布算法$f_m(x)=f_{m-1}(x)+T(x;\Theta (m)),\Theta (m)=arg\underset{\Theta (m)}{\min }(L(y,f_{m-1}(x_i)+\Theta (x_i,\Theta (m))$
   if loss function=均方误差损失，${\Theta }_m=(R_1,s_1),...,(R_j,s_j)=y-f_{m-1}(x);$commonly ，由lagrange中值公式，残差用$\partial L/\partial f_{m-1}(x)approach$

4. • EM——极大似然法的迭代求解(要选好初值点)，正确性与收敛性的证明，求导干极值点，高斯混合模型的期望表示+极大化，期望极大值对应F函数的极大-极大，迭代可以用其他方式，可用于无监督学习?

• recessive markov——根据隐变量表示出output的最大似然估计$P(i,o|\theta )$，计算其在$P(i,o|\overline{\theta })$下期望，\
  拉格朗日乘子法求极大值得\overline\theta，来估计o对应的i，

• 维比特算法用动态规划求得state 1,2,…,T（近似alg不能保证整体most probably）

• conditional random field——T为高维向量$(X,Y_w)$的随机过程(x,t)

  根据状态特征$s_l(y_i,x,w)$和transfer feature $t_k(y_{i-1},y_i,x,w)$定义条件随机场P(y|x)，可以用前向/back学习算法计算，$P(y_i|x)andP(y_i,y_{i+1}|x)$，针对$P_w(y|x)$的极大似然估计，梯度下降迭代得w，维比特算法得$y^{\ast }=argma{x}_y{P}_w(y|x)$

non-supervised learning

Preface

1. 无监督学习有聚类，降维，用于数据分析/监督学习的前处理

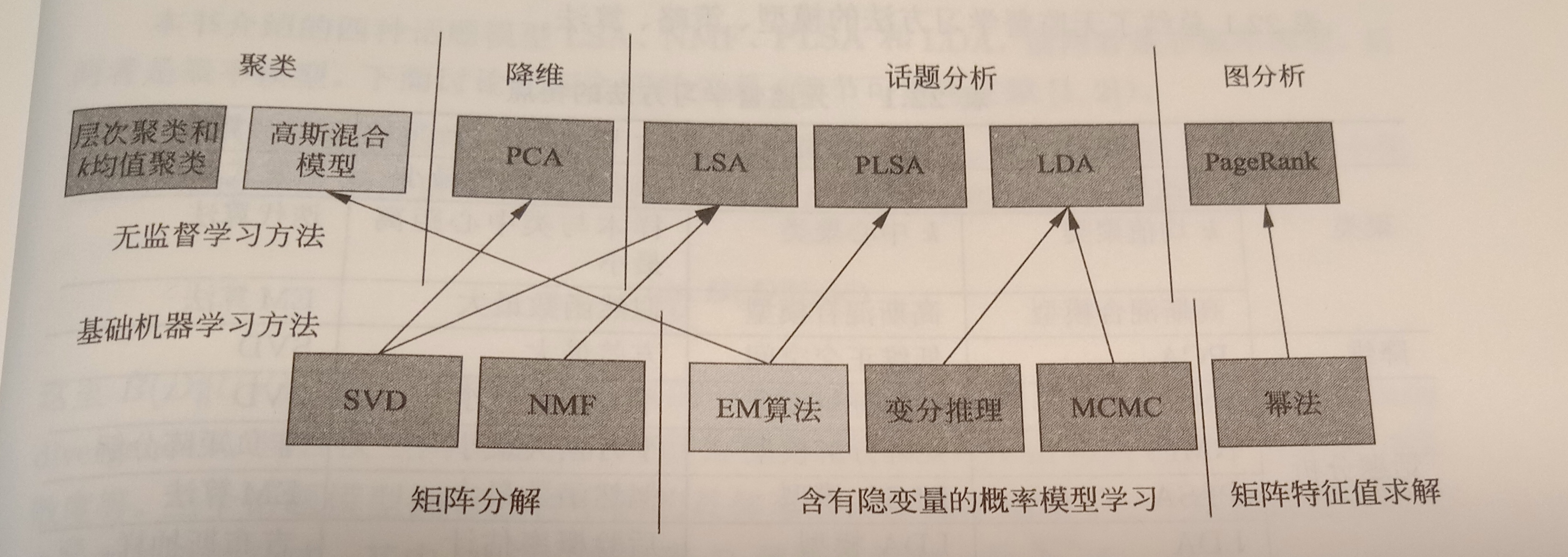
2. 监督学习的方法→层次聚类+k均值聚类
3. SVD用于LSA,SVD用于PCA

LSA

…

4. LSA👉PLSA，EM用于PLSA👉隐Markov model

• 以p(z|x)、p(y|x)为参量，单词-文本的出现次数为因变量，对数似然估计，数值解

5. 图的随机游走就是条件随机场吗？什么是PageRank

• 普通的markov模型，(p1,…,pk)ⁿ⁺¹=(p1,…,pk)ⁿ·A → 特征值分解后，类似裂项相消
• 平稳分布的充要性？非周期，不可约

Stochastic P review

• 问题与Improve——随机图上马尔科夫链未必具有平稳分布

​ ==？==添加一个等概率因子就可以避免

• 什么是迭代计算→名字，什么是代数计算👉R=dMR+$\frac{1-d}{n}\vec{1}$
• R模型已定，如果让我门估计，未知数为参量，用对数似然或平方为损失函数，梯度下降极值得估计

SVD的性质

6. 我们的终极Boss👉LDA