李超线段树-编程知识

李超线段树

概念

李超线段树是巨佬李超发明的一种可以求函数定点最值的线段树，又名李超树。代码简短，思想简明，用途广泛。

问题

李超线段树是用来解决类似于这种问题题目传送门

要求在平面直角坐标系下维护两个操作：

在平面上加入一条线段。记第 $i$ 条被插入的线段的标号为 $i$ 。
给定一个数 $k$ ，询问与直线 $x = k$ 相交的线段中，交点纵坐标最大的线段的编号。

思路

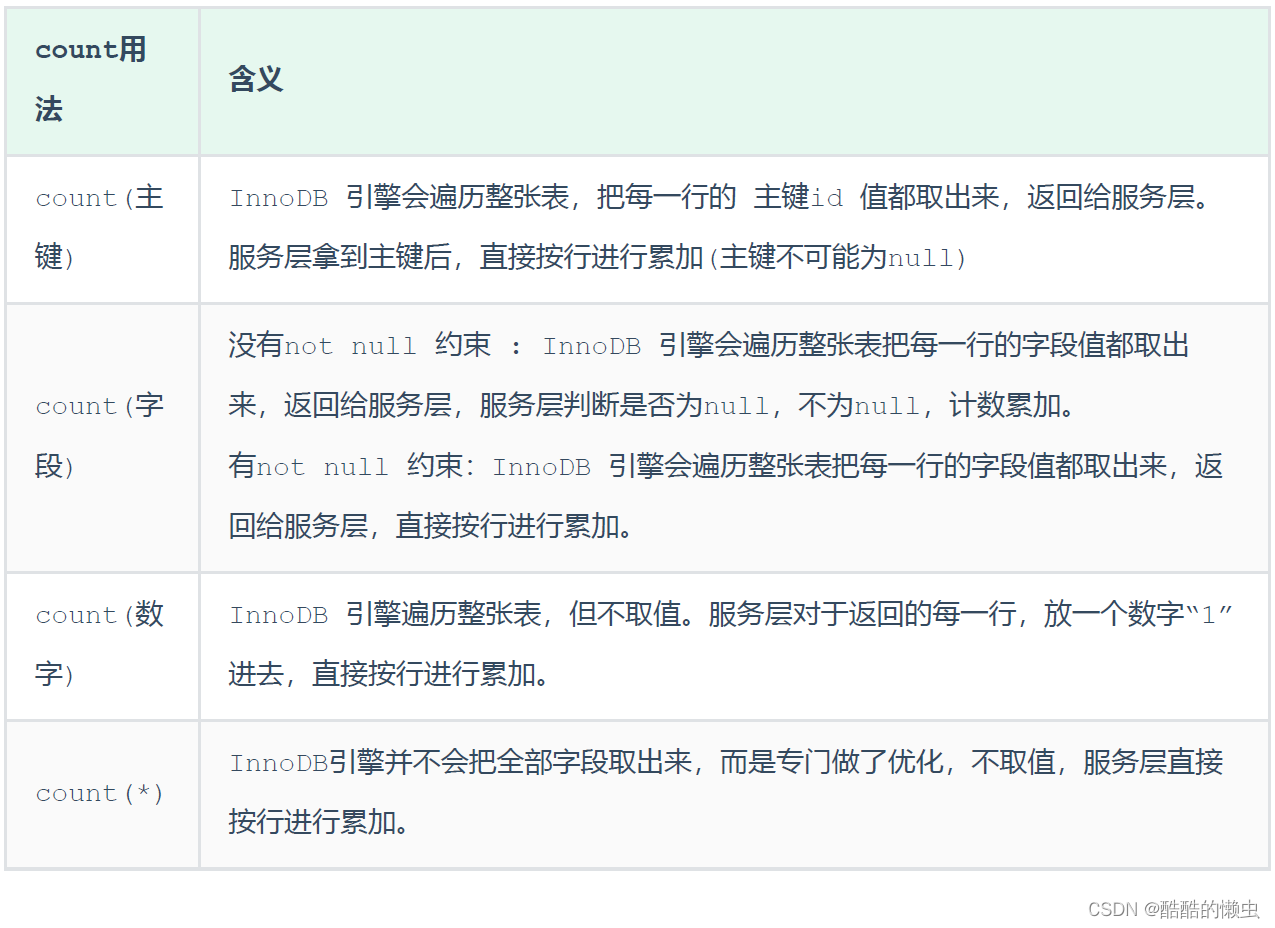
李超线段树的结构和普通线段树一样的，只是它每个节点存的是该区间优势最大的线段

区间 $[L, R]$ 中，蓝色折线为最高折线，绿色线段为该区间的优势最大线段。

插入操作

对于一个区间，它被线段覆盖的情况可以分为六种：

1、线段覆盖的区间和该区间不相交，直接返回

2、线段覆盖部分该区间，递归到左右子区间继续处理；

3、线段完全覆盖该区间：线段在两个端点处值均比之前保存的优势线段更大，则替换优势线段，返回；

4、线段在两个端点处的值均比之前的保存的优势线段小，则返回 5、线段在两个端点处与之前保存的优势线段比较，如果在中点处更优，则更新优势线段(交换两线段)；

6、然后再判断左右端点处的值，如果该侧优势线段不占优势，则递归该侧。

查询

它维护的是区间中点处的最大(最小）值的线段，采用 标记永久化。所谓标记永久化是指标记不下传，查询时，需要由该节点及其所有祖先的标记综合起来才能得出答案。

因为李超树每个区间保存的只是当前区间的中点的最大值，所以它的标记是不能下传的，下传了反而不准确。

每个区间保存的只是区间处占优势的线段的编号。(另有一个线段的数组，记录了每条线段的斜率和截距)。优势线段仅仅只是中点更优，并不是处处占优，也不是端点占优。

适合单点查询，查询时必须要将叶节点的所有祖先的优势线段在该处进行比较。

例题

[P4097 【模板】李超线段树 / HEOI2013] Segment - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

版题。 ~~可以感性理解一下~~

#include <bits/stdc++.h>
#define fu(x , y , z) for(int x = y ; x <= z ; x ++)
#define lp p<<1
#define rp p<<1|1
using namespace std;
const int N = 1e5 + 5 , mod = 39989 , my = 1000000000;
const double eps = 1e-8;
int l[N << 3] , r[N << 3] , tr[N << 3] , tot;
double k[N] , b[N];
inline int dcmp(double x) {return fabs(x) <= eps ? 0 : x < 0 ? -1 : 1;// fabs (x) <= eps 
}
double f (int x , int p) { return 1.0 * k[x] * p + b[x]; }
bool pd (int x , int y , int p) {double fx = f(x , p) , fy = f (y , p);// return fabs (fy - fx) >= eps ? fx < fy : x > y; // return dcmp(fx-fy) ? fx < fy : x > y;return fx <= fy;
}
void build (int p , int ll , int rr) {l[p] = ll , r[p] = rr;if (ll == rr) return;int mid = (ll + rr) >> 1;build (lp , ll , mid);build (rp , mid + 1 , rr);
}
void change (int p , int ll , int rr , int x) {if (r[p] < ll || rr < l[p]) return;if (ll <= l[p] && r[p] <= rr) {if (pd (x , tr[p] , l[p]) && pd (x , tr[p] , r[p])) return;if (pd (tr[p] , x , l[p]) && pd (tr[p] , x , r[p])) {tr[p] = x;return;}int mid = (l[p] + r[p]) >> 1;if (pd (tr[p] , x , mid)) swap (tr[p] , x);if (pd (tr[p] , x , l[p])) change (lp , l[p] , r[p] , x);else change (rp , l[p] , r[p] , x);return;}change (lp , ll , rr , x) , change (rp , ll , rr , x);
}
int query (int p , int x) {if (x < l[p] || r[p] < x) return 0;if (l[p] == r[p] && l[p] == x) return tr[p];int mid = (l[p] + r[p]) >> 1 , res = 0;if (x <= mid) res = query (lp , x);else res = query (rp , x);// res = x <= mid ? query(lp,x) : query(rp,x);if (pd (res , tr[p] , x)) res = tr[p];return res;
}
int main () {int T;scanf ("%d" , &T);int op , x , lst = -1 , y , xx , yy;build (1 , 1 , 40000);while (T --) {scanf ("%d" , &op);if (!op) {scanf ("%d" , &x);x = (x + lst + mod) % mod + 1;// cout << x << "\n";lst = query (1 , x);printf ("%d\n" , lst);lst --;// if (lst) lst --;}else {scanf ("%d%d%d%d" , &x , &y , &xx , &yy);x = (x + lst + mod) % mod + 1 , xx = (xx + lst + mod) % mod + 1;y = (1ll * y + lst + my) % my + 1 , yy = (1ll * yy + lst + my) % my + 1;if (xx < x) swap (xx , x) , swap (yy , y);tot++;if (x == xx) k[tot] = 0 , b[tot] = max (y , yy);else k[tot] = (double)(yy - y) / (xx - x) , b[tot] = yy - k[tot] * xx;change (1 , x , xx , tot);  }}return 0;
}