堆优化迪氏最短单源路径原理及C++实现-编程知识

堆优化迪氏最短单源路径原理及C++实现

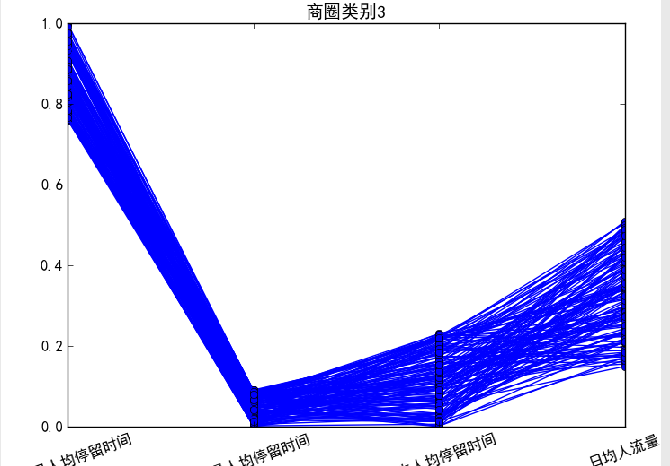
时间复杂度

O(ElogE)，E是边数。适用与稀疏图。

使用前提

边的权为正。可以非连通，非连通的距离为-1。

原理

优选队列（小根堆）记录两个数据：当前点到源点距离，当前点。先处理距离小的点；如果距离相等，先处理谁都可以。可以用pair记录，不用重写小于。优先队列只记录如下情况的距离：
一，{0，源点}。
二，任意点的最短距离和可以直达的边。
如果是有向图，则入队数量等于边数，计算出起点最短路径的那一轮。无向图，则翻倍。显然出队数量等于入队数量。优先队列入队和出队时间复杂度都是O(logn)，故总时间复杂度为O(nlogn)。

样例

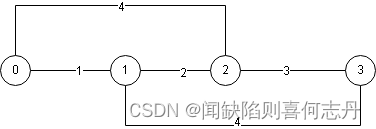
下表分析源点为0的处理过程。


初始	入队{0,0}
出队{0,0}	入队{1,1}	0到源点的最短距离为0
	入队{4,2}
出队{1,1}	入队{2,0}
	入队{3,2}	1到源点的最短距离为1
	入队{5,3}
出队{2,0}	0已经处理
出队{3,2}	入队{7,0}	2到源点最短距离为3
	入队{5,1}
	入队{6,3}
出队{4,2}	2已经处理
出队{5,1}	1已经处理
出队{5,3}	… 3到源点的最短距离是5。
…

核心代码

非常的简洁。
typedef pair<long long, int> PAIRLLI;
class CHeapDis
{
public:
   CHeapDis(int n)
   {
       m_vDis.assign(n, -1);
   }
   void Cal( int start, const vector<vector<pair<int, int>>>& vNeiB)
   {
       std::priority_queue<PAIRLLI, vector<PAIRLLI>, greater<PAIRLLI>> minHeap;
       minHeap.emplace(0, start);
       while (minHeap.size())
       {
           const long long llDist = minHeap.top().first;
           const int iCur = minHeap.top().second;
           minHeap.pop();
           if (-1 != m_vDis[iCur])
           {
               continue;
           }
           m_vDis[iCur] = llDist;
           for (const auto& it : vNeiB[iCur])
           {
               minHeap.emplace(llDist + it.second, it.first);
           }
       }
   }
   vector<long long> m_vDis;
};

测试用例

#include <iostream>
#include <vector>
#include <queue>
#include <assert.h>
using namespace std;

class CDebugDis : public CHeapDis
{
public:
   using CHeapDis::CHeapDis;
   void Assert(const vector<int>& vDis)
   {
       for (int i = 0; i < vDis.size(); i++)
       {
           assert(vDis[i] == m_vDis[i]);
       }
   }
};

struct CDebugParam
{
   int n;
   vector<vector<std::pair<int, int>>> edges;
   int s;
   vector<int> dis;//答案
};

int main()
{
   vector<CDebugParam> params = { {1,{{}},0,{0}},
       {2,{{}},0,{0,-1}},{2,{{{1,2}},{{0,2}}},0,{0,2} }
       ,{3,{{{1,4},{2,5}},{{0,4}},{{0,5}}},0,{0,4,5} }
       ,{3,{{{1,4},{2,8}},{{0,4},{2,3}},{{0,8},{1,3}}},0,{0,4,7} }
       ,{3,{{{1,4},{2,8}},{{0,4},{2,5}},{{0,8},{1,5}}},0,{0,4,8} }
       ,{4,{{{1,1},{2,4}},{{0,1},{2,2},{3,4}},{{0,4},{1,2},{3,3}},{{1,4},{2,3}}},0,{0,1,3,5}}
   };
   for (const auto& par : params)
   {
       CDebugDis n2Dis(par.n);
       n2Dis.Cal(par.s, par.edges);
       n2Dis.Assert(par.dis);
   }
}