数据结构--队列与循环队列的实现-编程知识

数据结构–队列的实现

1.队列的定义

比如有一个人叫做张三,这天他要去医院看病,看病时就需要先挂号,由于他来的比较晚,所以他的号码就比较大,来的比较早的号码就比较小,需要到就诊窗口从小号到大依次排队,前面的小号就诊结束之后,才会轮到大号来,小号每就诊完毕就销毁,每新来一个病人就会顺着向后增加一个较大的号码,这些号码就构成了队列.

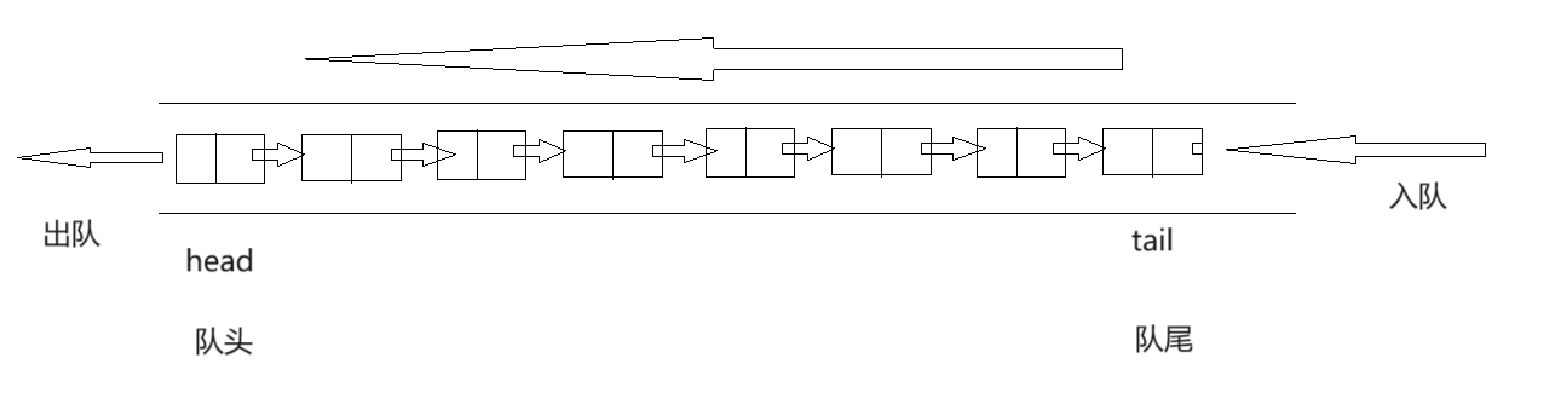
所谓队列就是一种先进先出的数据结构,例如在例子中,先来挂号的病人先就诊,后来的病人后就诊,队列是只允许在一端进行插入操作,而在另一端进行删除操作的线性表,队列是一种先进先出的线性表,允许插入数据的一端称之为队尾,允许删除数据的一端称之为队头.**假设队列中的元素是{a,b,c,d,e,f,g}那么a就是队头元素,g就是队尾元素,这样删除时就可以总是从a处开始,插入数据时从g开始,也比较符合我们的日常生活习惯.

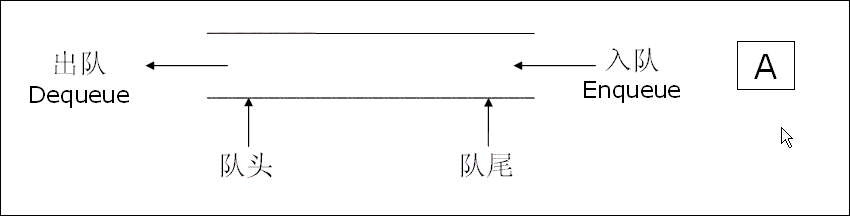
在这里插入图片描述

队列在生活中的使用非常频繁.

2.队列的实现

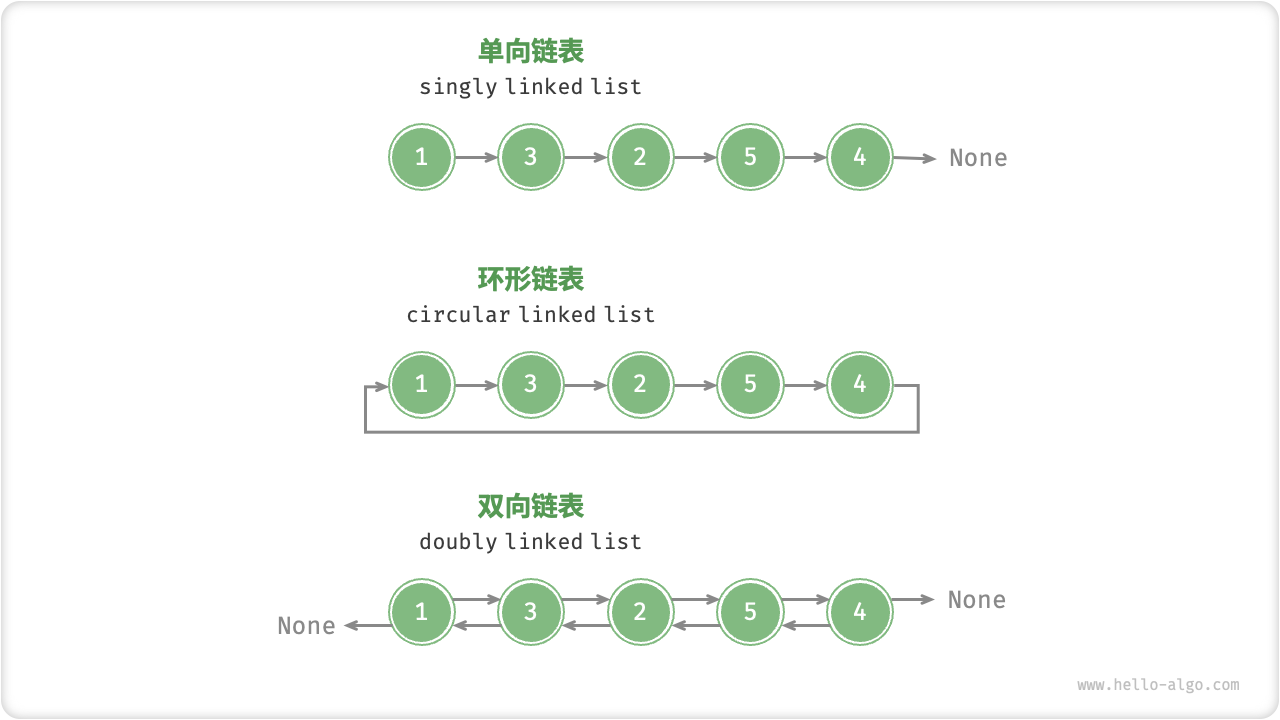
队列实际上也是线性表,但是队列的操作与栈是不同的,队列的对于数据的插入操作是在队尾进行的,对数据的删除操作是在队头进行,那么由此可以想到,对于有这种特点的队列,使用链表的结构更加方便,因为链表的头删和尾插的效率非常高,不需要像数组那样挪动数据.

2.1节点的定义

每个节点需要存储数据和下一个节点的地址.

typedef struct QueueNode//此处定义的是每个节点的结构
{struct QueueNode* next;QDataType data;
}QueueNode;

由于我们是对每个节点之间的链接关系进行处理,所以就需要定义结构体的指针对节点中的next指针进行操作,所以我们可以定义head和tail两个结构体指针,head指针指向链表的第一个节点,tail指针指向链表的最后一个节点.那么就可以将这两个节点也包装成一个结构体:

typedef struct Queue//将两个指针包装成一个结构体
{QueueNode* head;QueueNode* tail;
}Queue;

在这里插入图片描述

2.2队列的初始化

void QueueInit(Queue* pq)//初始化队列
{assert(pq != NULL);pq->head = NULL;pq->tail = NULL;
}

2.3判断队列是否为空

bool QueueEmpty(Queue* pq)
{assert(pq);return pq->head == NULL;
}

2.4队列的销毁

void QueueDestroy(Queue* pq)
{assert(pq);QueueNode* cur = pq->head;//while (cur != NULL){QueueNode* next = cur->next;free(cur);cur = next;}pq->head = pq->tail = NULL;
}

2.5插入数据

void QueuePush(Queue* pq, QDataType x)//插入数据
{assert(pq);QueueNode* newnode = (QueueNode*)malloc(sizeof(QueueNode));if (newnode == NULL){printf("malloc fail!");exit(0);}newnode->data = x;newnode->next = NULL;if (pq->head == NULL){pq->head = pq->tail = newnode;}else{pq->tail->next = newnode;//连接两个节点pq->tail = newnode;//新的尾节点}
}

2.6删除队头数据

删除队头数据之前要判断队列是否为空队列,如果队列是空队列就无法进行删除操作.

void QueuePop(Queue* pq)//删除数据
{assert(!QueueEmpty(pq));//队列不能为空QueueNode* next = pq->head->next;free(pq->head);pq->head = next;//假如链表已经被删完了，此刻要将tail也置为空指针if (pq->head == NULL){pq->tail = NULL;}
}

2.7取出队尾数据

QDataType QueueBack(Queue* pq)//取出队尾的数据
{assert(pq);assert(!QueueEmpty(pq));return pq->tail->data;
}

2.8取出队头数据

QDataType QueueFront(Queue* pq)//获取头的数据
{assert(pq);assert(!QueueEmpty(pq));return pq->head->data;
}

2.9获取队列的节点的个数

int QueueSize(Queue* pq)
{assert(pq);int n = 0;QueueNode* cur = pq->head;while (cur != NULL){n++;cur = cur->next;}return n;
}

3.循环队列

3.1循环队列的设计

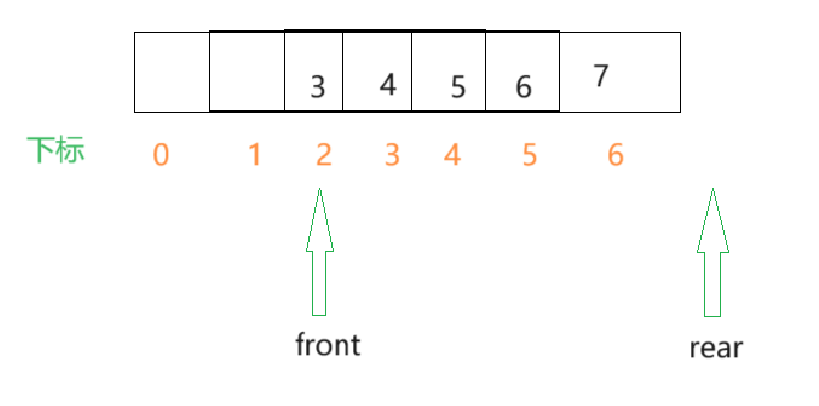
假定我们是使用的数组实现队列.那么假设一个队列含有n个元素,我们就需要创建一个元素个数大于n的数组.并将队列中的数据存储在数组的前n个单元,数组下标为0的一端就是队头,另一端就是队尾.
为了方便,我们设置两个变量,一个front用于存储队头数据的下标,也就是0,另一个rear变量用于存储队尾的元素的下一个位置.当需要取出队头元素时,就需要除了队头之外的所有数据都需要向前移动一格.

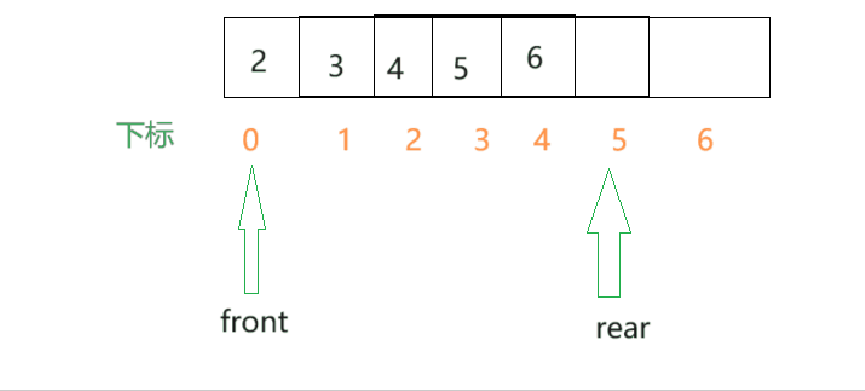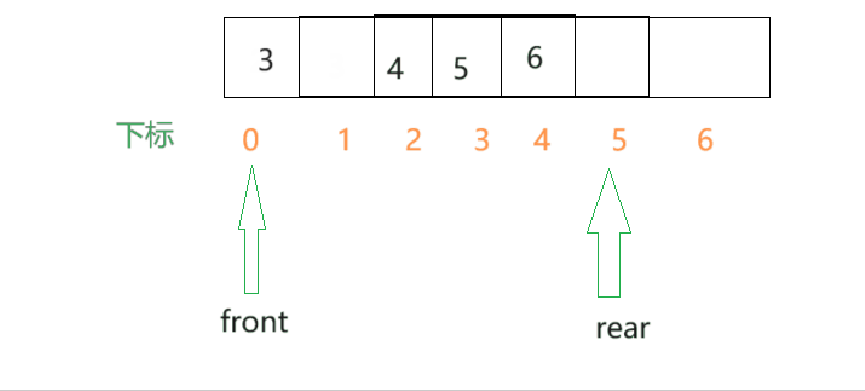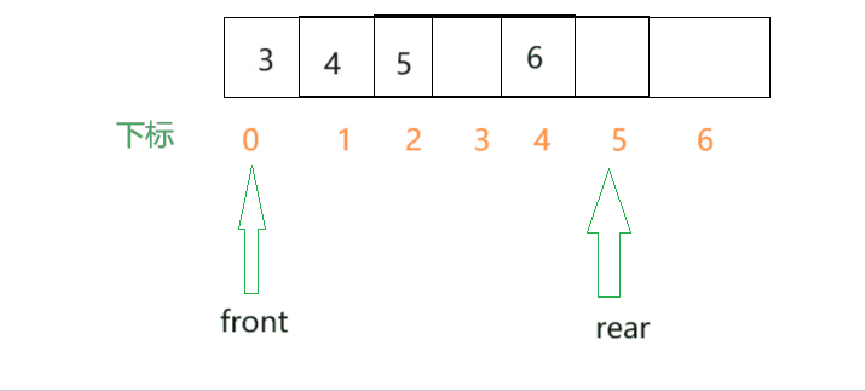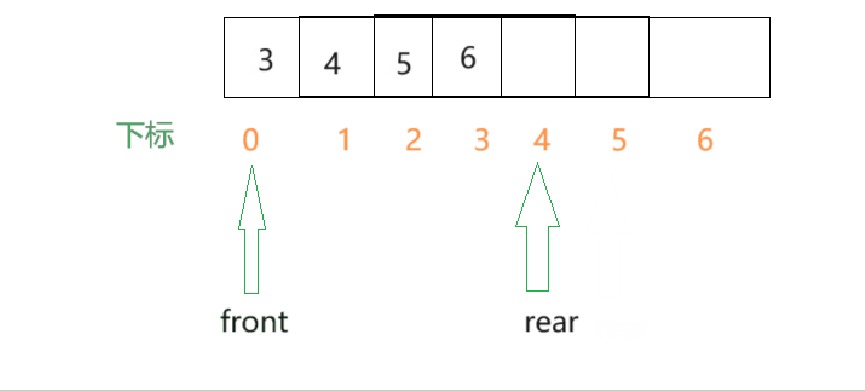
在这里插入图片描述

由此看来,效率是不高的,所以这里可以改进,让front指针移动起来,队头每出一个元素,front就向后移动一个单位.

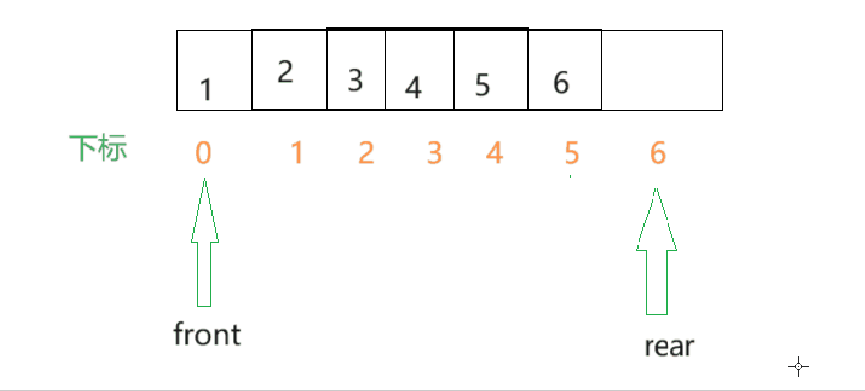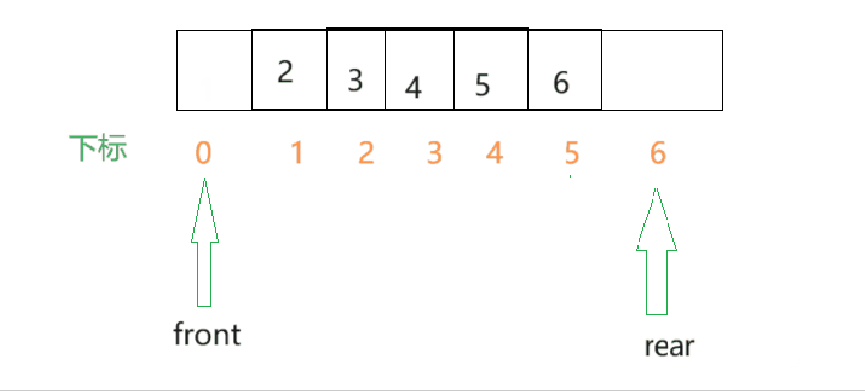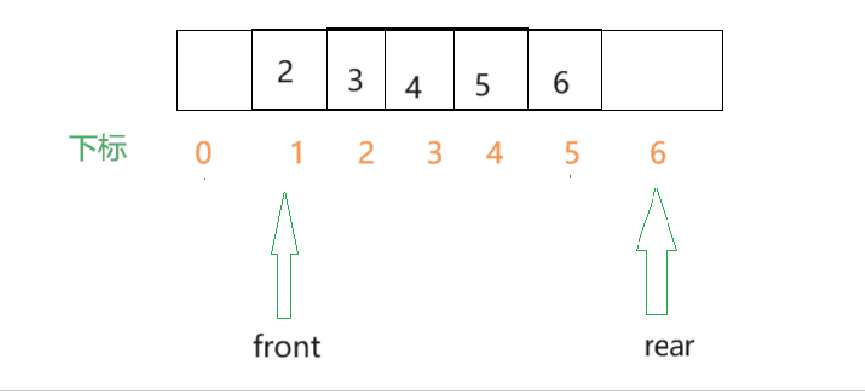
在这里插入图片描述

假设数组一开始是空的,那么front和rear一开始的值就都是0,每插入一个元素,rear就向后移动.

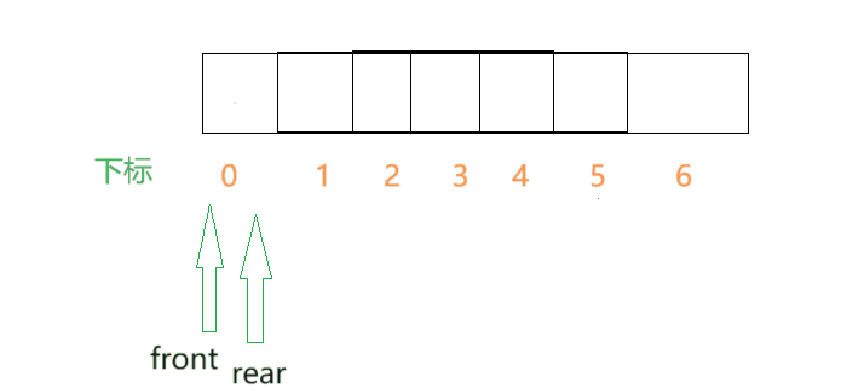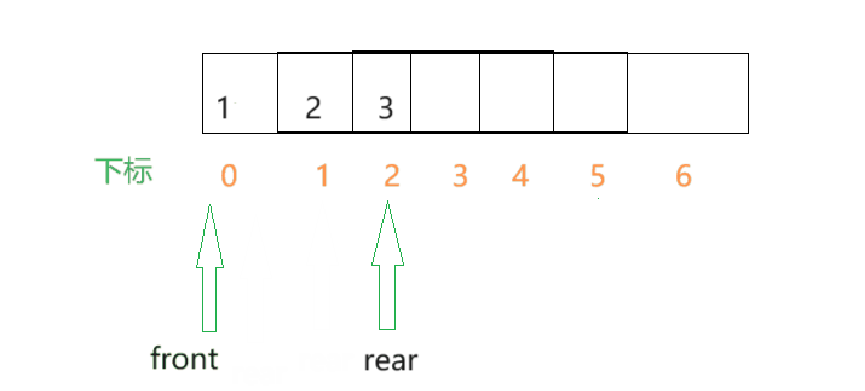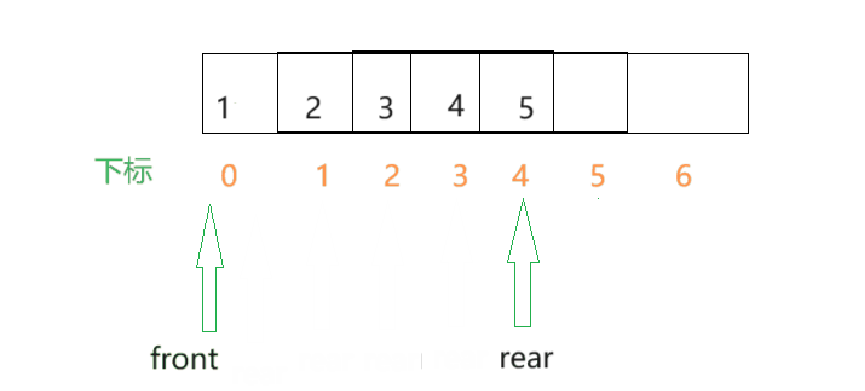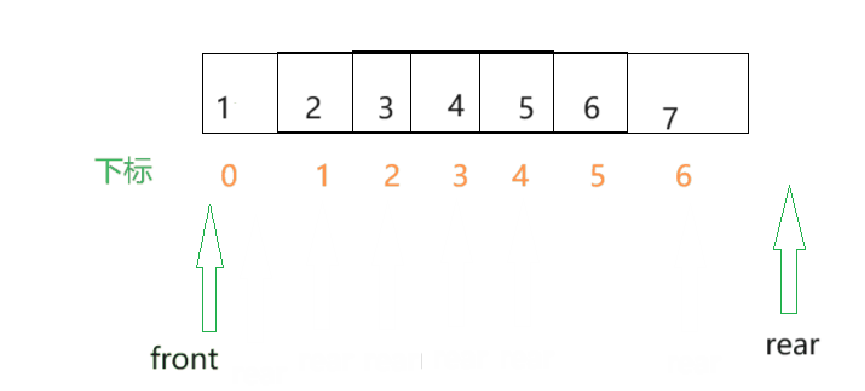
在这里插入图片描述

但是此时的rear就移动到了数组之外的空间了,假如此刻数组中的数据都已经满了,然而继续向其中插入数据,就出现了越界问题.

假如是以下这种情况呢??
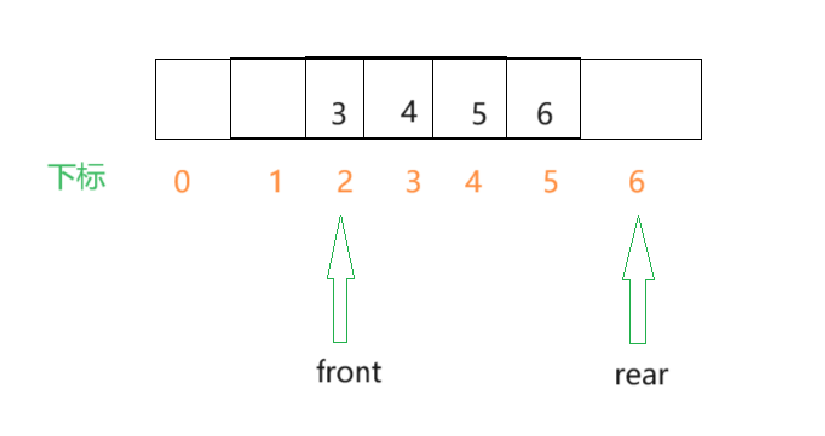
在这里插入图片描述

此刻向rear位置插入数据之后,此时的数组的0和1位置处是空的,那此时rear若再向后加,就显得有点蠢了,因为数组中的前面是空着的却不用.

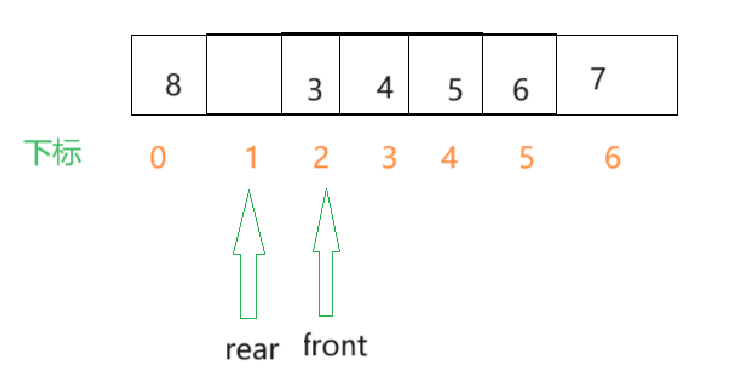
解决办法:当rear快越界时,接着让rear从数组的第一个元素开始,构成循环,这就是循环队列.例如在下面这种情况,将rear改为0时比较好的.

那此刻我们接着向队列中插入元素.
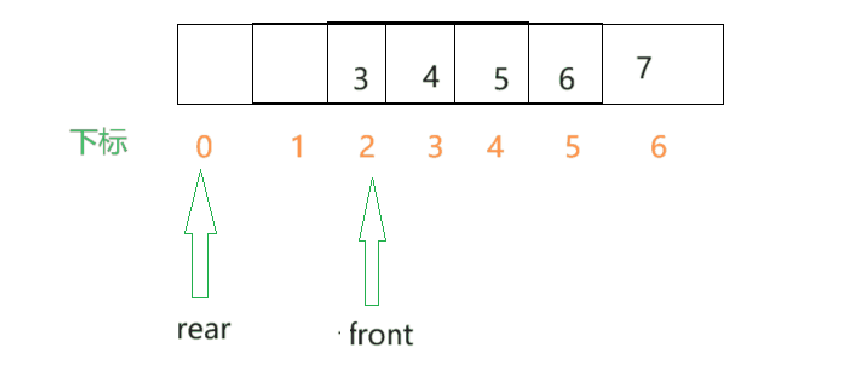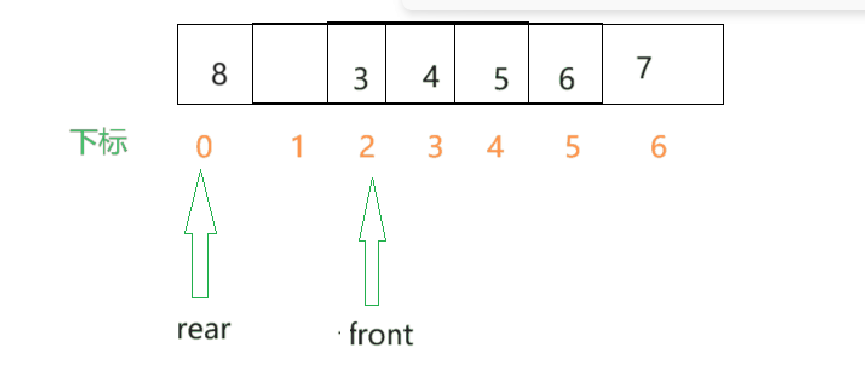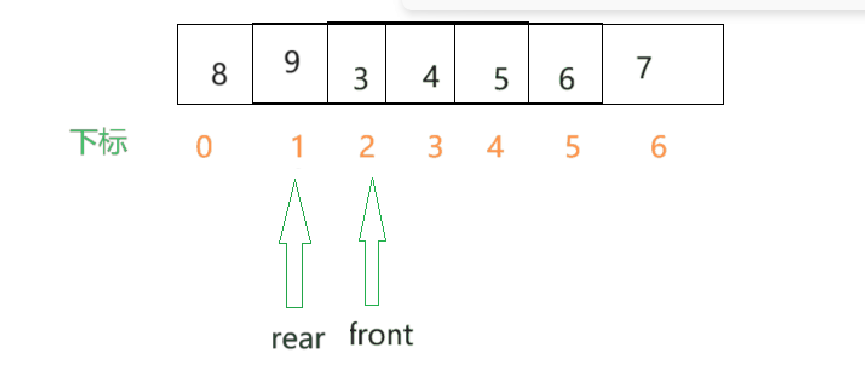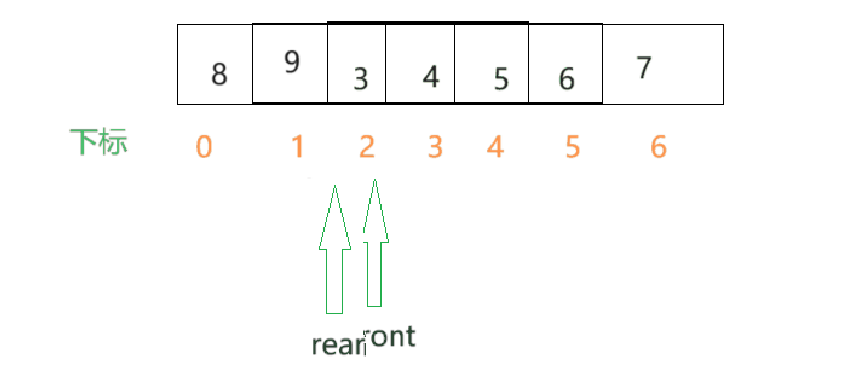
在这里插入图片描述

不难发现,当队列满了之后,rear和front是指向同一个下标的(即rear == front).在队列为空时,rear和front指向的是同一个下标(rear == front),那么什么情况队列是满什么情况队列是空就无法确切的判断了.

解决方案:当队列为空时,条件是rear == front,当队列为满时,保留一个元素的空间,在数组中留一个空闲单元,如下图所示,此刻的队列就已经满了.假设数组的最大容量是N个单位,那么队列为满的条件就是 (rear+1)%N == front.

由此可推断出:在容量为N的数组中,存储的元素个数为:(rear-front+N)%N

3.2循环队列的元素的创建

这里定义一个MAX常量用于记录队列中的元素个数,实际上的数组需要MAX个单位的空间.

typedef int QDataType;
typedef struct Queue {QDataType a[MAX+1];int front;int rear;
}Queue;

3.3循环队列的初始化

//队列的初始化
void InitQueue(Queue* q)//含有MAX个元素的队列,开辟MAX+1个单位空间
{q->front = q->rear = 0;
}

3.4取出队头元素

//出队列
QDataType DeQueue(Queue* q)
{assert(!QueueEmpty(q));QDataType ret = q->a[q->front];q->front = (q->front + 1) % (MAX + 1);return ret;
}

3.5向队尾插入元素

//入队列
void EnQueue(Queue* q, QDataType* x)
{assert(!QueueFull(q));q->a[q->rear] = x;q->rear = (q->rear + 1) % (MAX + 1);
}

3.6队列中存储的元素个数

//队列的元素个数
int QueueSize(Queue* q)
{return (q->rear - q->front + MAX + 1) % (MAX + 1);
}

3.7判断队列是否为空

//判断队列是否为空
bool QueueEmpty(Queue* q)
{return q->front == q->rear;
}

3.8判断队列是否为满

bool QueueFull(Queue* q)
{return (q->rear + 1) % (MAX + 1) == q->front;
}

4.链式队列和循环队列的比较

循环队列是事先申请好空间,使用期间无法释放,而链式队列则不存在这个问题.虽然链式队列在空间上会有更多的开销,但是也在可接受范围之内.所以在空间上,链式队列更加灵活.