目录
- 1143.最长公共子序列
- 思路
- 代码
- 1035.不相交的线
- 思路
- 代码
- 53. 最大子序和(dp)
- 思路
- 代码
1143.最长公共子序列
Leetcode

思路
本题和718. 最长重复子数组 区别在于这里不要求是连续的了,但要有相对顺序,即:“ace” 是 “abcde” 的子序列,但 “aec” 不是 “abcde” 的子序列。
不是连续的话,具体写代码的区别体现在递推公式上,
if text1[i - 1] != text2[j - 1]: dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])
从下图可以看出来可以有三个方向推导出dp[i][j]
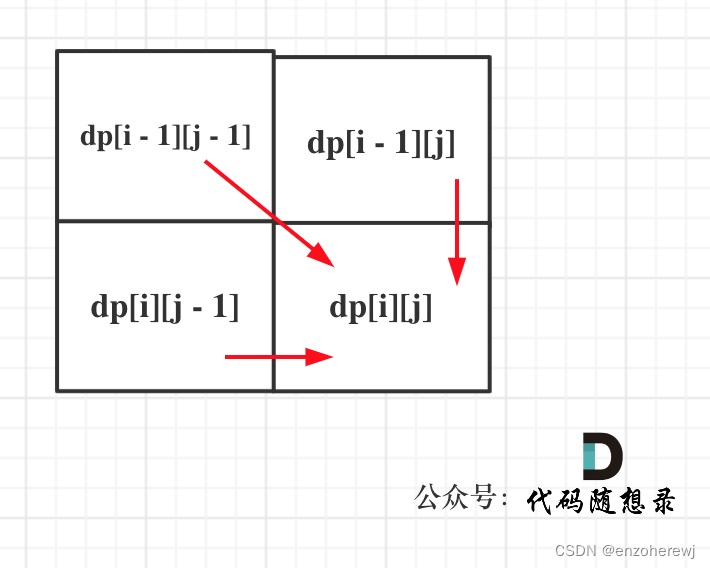
举例推导dp数组
以输入:text1 = “abcde”, text2 = “ace” 为例,dp状态如图:
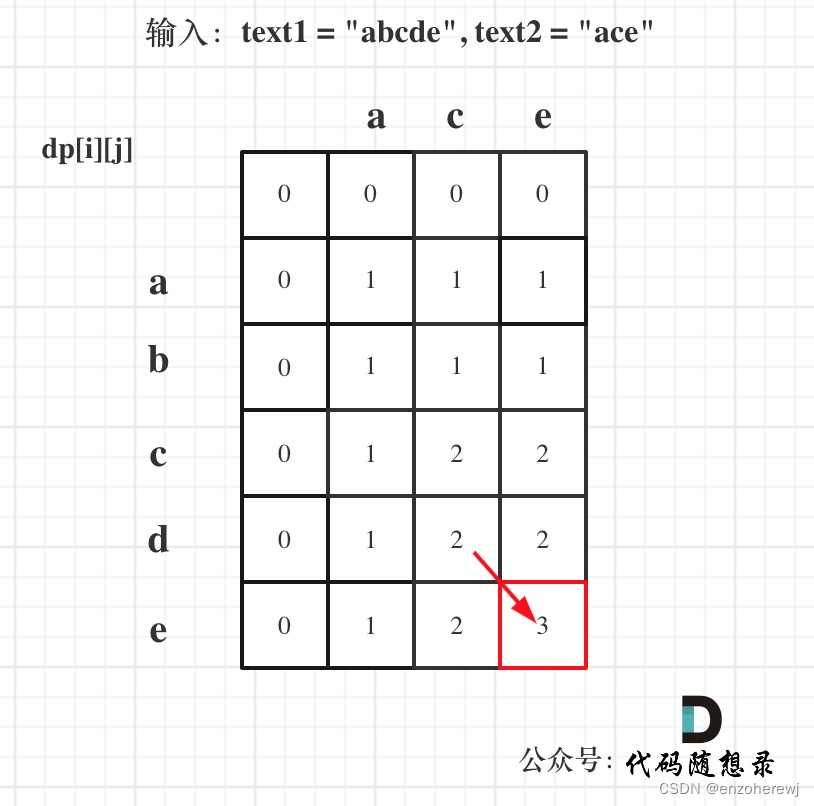
代码
class Solution:def longestCommonSubsequence(self, text1: str, text2: str) -> int:dp = [[0] * (len(text1) + 1) for _ in range(len(text2) + 1)]for i in range(1, len(text2) + 1):for j in range(1, len(text1) + 1):if text2[i - 1] == text1[j - 1]:dp[i][j] = dp[i - 1][j - 1] + 1else:dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])return dp[-1][-1]
- 时间复杂度:
O(n * m),其中 n 和 m 分别为 text1 和 text2 的长度 - 空间复杂度:
O(n * m)
1035.不相交的线
Leetcode

思路
此题和上题一模一样。
代码
class Solution:def maxUncrossedLines(self, nums1: List[int], nums2: List[int]) -> int:dp = [[0] * (len(nums1) + 1) for _ in range(len(nums2) + 1)]for i in range(1, len(nums2) + 1):for j in range(1, len(nums1) + 1):if nums2[i - 1] == nums1[j - 1]:dp[i][j] = dp[i - 1][j - 1] + 1else:dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])return dp[-1][-1]
53. 最大子序和(dp)
Leetcode

思路
- dp[i]:包括下标i(以nums[i]为结尾)的最大连续子序列和为dp[i]。
- 递推公式:
dp[i]只有两个方向可以推出来:dp[i - 1] + nums[i],即:nums[i]加入当前连续子序列和nums[i],即:从头开始计算当前连续子序列和
我一开始写成了dp[i] = max(dp[i], dp[i - 1] + nums[i]),那这就不对了,因为这样就会受到dp[i]初始化的影响。
- 初始化:dp[0] = nums[0],剩下的随意
- 遍历顺序从前往后
- 举例
以示例一为例,输入:nums = [-2,1,-3,4,-1,2,1,-5,4],对应的dp状态如下:
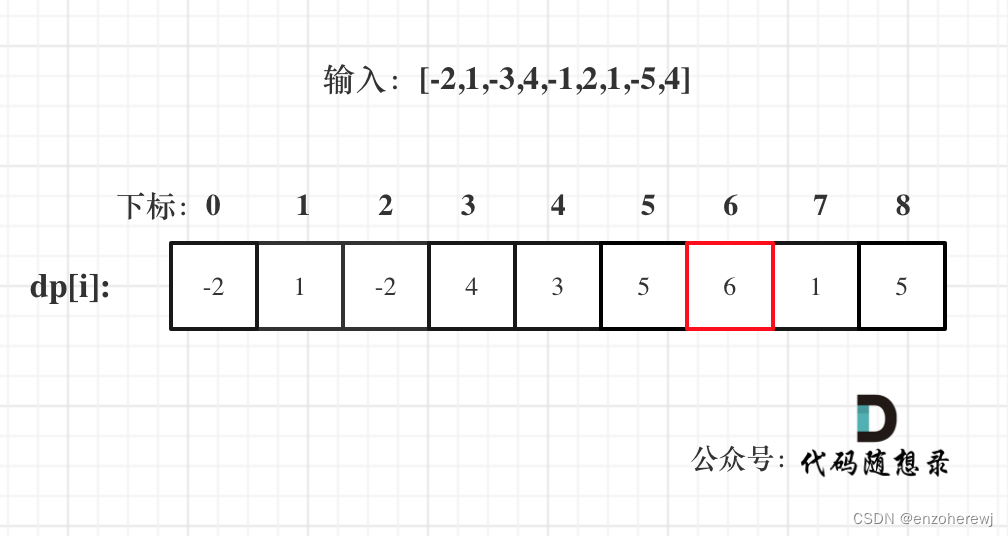
代码
class Solution:def maxSubArray(self, nums: List[int]) -> int:dp = [nums[0]] * len(nums)res = nums[0]for i in range(1, len(nums)):dp[i] = max(nums[i], dp[i - 1] + nums[i])res = max(res, dp[i])return res
- 时间复杂度:
O(n) - 空间复杂度:
O(n)