《Dataset Condensation with Differentiable Siamese Augmentation》

在本文中，我们专注于将大型训练集压缩成显著较小的合成集，这些合成集可以用于从头开始训练深度神经网络，性能下降最小。受最近的训练集合成方法的启发，我们提出了可微暹罗增强方法，它可以有效地利用数据增强来合成更具信息的合成图像，从而在使用增强方法训练网络时获得更好的性能。在多个图像分类基准上的实验表明，该方法在CIFAR10和CIFAR100数据集上取得了较先进水平的显著提高，提高了7%。结果表明，该方法在MNIST、FashionMNIST、SVHN、CIFAR10上的相对性能分别为99.6%、94.9%、88.5%、71.5%，数据量不到1%。

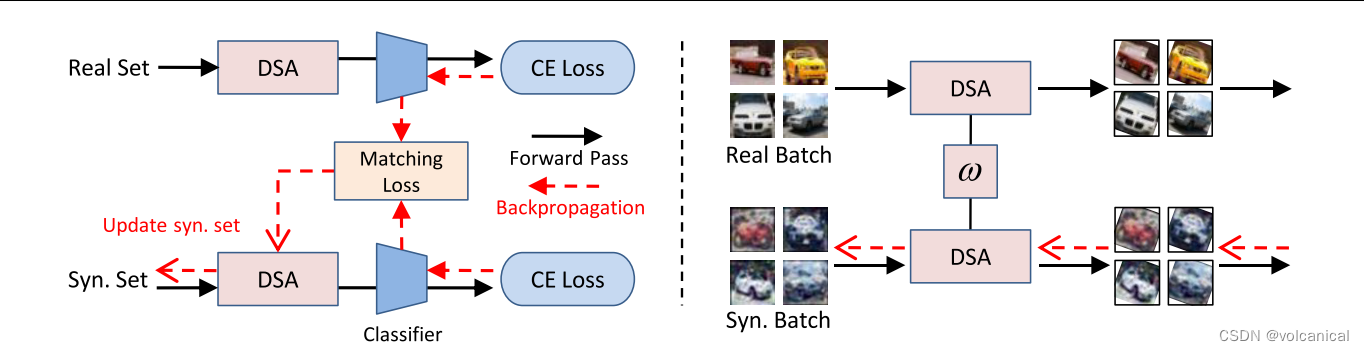
方法：

1. 简单介绍DC（Data Condensation）

假设我们有一个巨大的训练集 $\mathcal{T}=$ $\left\{\left({\mathbf{x}}_1,y_1\right),\dots ,\left({\mathbf{x}}_{|\mathcal{T}|},y_{|\mathcal{T}|}\right)\right\}$ 其中有 $|\mathcal{T}|$ 个图片和标签对. DC (Zhao et al., 2021)目标是学习一个更小的数据集 $|\mathcal{S}|$ 生成图片和标签对。 $\mathcal{S}=$ $\left\{\left({\mathbf{s}}_1,y_1\right),\dots ,\left({\mathbf{s}}_{|\mathcal{S}|},y_{|\mathcal{S}|}\right)\right\}$ 来自于（通过学习） $\mathcal{T}$ 并且在数据集 $\mathcal{S}$ 上训练的神经网络效果和在 $\mathcal{T}$ 上训练得到的神经网络效果接近。 用 ${\varphi }_{{\mathbf{\theta }}^{\mathcal{T}}}$ 和 ${\varphi }_{{\mathbf{\theta }}^{\mathcal{S}}}$ 表示深度神经网络，其参数分别为 ${\mathbf{\theta }}^{\mathcal{T}}$ 和 ${\mathbf{\theta }}^{\mathcal{S}}$，分别在训练集 $\mathcal{T}$ 和 $\mathcal{S}$ 上训练得到。DC的目标是如下方程:
$$\begin{array}{c}{\mathbb{E}}_{\mathbf{x}\sim P_{\mathcal{D}}}\left[\ell \left({\varphi }_{{\mathbf{\theta }}^{\tau }}(\mathbf{x}),y\right)\right]\simeq {\mathbb{E}}_{\mathbf{x}\sim P_{\mathcal{D}}}\left[\ell \left({\varphi }_{{\mathbf{\theta }}^{\mathcal{S}}}(\mathbf{x}),y\right)\right]\end{array}$$
在真实数据分布 $P_{\mathcal{D}}$ 上的损失 $\ell$ (i.e. cross-entropy loss)。

在浓缩数据集 $\mathcal{S}$ 上训练得到的模型参数要尽可能接近原始数据集的结果, i.e. ${\mathbf{\theta }}^{\mathcal{S}}\approx {\mathbf{\theta }}^{\mathcal{T}}$。

然后作者就开始举例DC有哪些不好的地方。

例如：

1. 在每一轮都假设${\mathbf{\theta }}_t^{\mathcal{T}}$ 和 ${\mathbf{\theta }}_t^{\mathcal{S}}$相等，继续训练。
2. 只对一个模型进行提取。

2. DSA

方法就是在DC前面套了一层数据增强，可微的数据增强

进入正题，那么本文提出的DSA，可微暹罗增强（我也不知道为什么是暹罗）

2.1 暹罗增强

首先是暹罗增强，在图片数据中基本就是裁剪，旋转，颜色变换等
$$\underset{\mathcal{S}}{\min }D\left({\nabla }_{\mathbf{\theta }}\mathcal{L}\left(\mathcal{A}\left(\mathcal{S},{\omega }^{\mathcal{S}}\right),{\mathbf{\theta }}_t\right),{\nabla }_{\mathbf{\theta }}\mathcal{L}\left(\mathcal{A}\left(\mathcal{T},{\omega }^{\mathcal{T}}\right),{\mathbf{\theta }}_t\right)\right)$$
此处${\omega }^{\mathcal{T}}$和${\omega }^{\mathcal{S}}$分别代表了在两个数据集上进行的数据增强参数。然后作者指出，如果使用随机分布的${\omega }^{\mathcal{T}}$和${\omega }^{\mathcal{S}}$会导致训练无法收敛，因此在文中使用的${\omega }^{\mathcal{T}}={\omega }^{\mathcal{S}}$。

那么因为，浓缩数据集$\mathcal{S}$和原始数据集$\mathcal{T}$肯定是不一样的，那就没有一个一对一的关系，来进行同样的数据增强，那么文中的方法就是，一个batch的数据使用一样的数据增强。一个batch里$\mathcal{S}$和$\mathcal{T}$相互对应。

2.2 可微增强

要让这个过程可以BP训练，那么这个数据增强必须是可以微分的，即：
$$\frac{\partial D(\cdot )}{\partial \mathcal{S}}=\frac{\partial D(\cdot )}{\partial {\nabla }_{\mathbf{\theta }}\mathcal{L}(\cdot )}\frac{\partial {\nabla }_{\mathbf{\theta }}\mathcal{L}(\cdot )}{\partial \mathcal{A}(\cdot )}\frac{\partial \mathcal{A}(\cdot )}{\partial \mathcal{S}}$$

Traditionally transformations used for data augmentation are not implemented in a differentiable way, as optimizing input images is not their focus. Note that all the standard data augmentation methods for images are differentiable and can be implemented as differentiable layers.

这里是不是有点自相矛盾，传统数据增强变换实现不是可微的，但是图像上的标准数据增强方法是可微的？

2.3 训练过程

和DC基本一致，最外层训练K负责训练不同的模型初始化以增强浓缩数据集适用性，内层不断更新模型，训练T-1步，最内层是对每一个标签进行训练更新数据集。

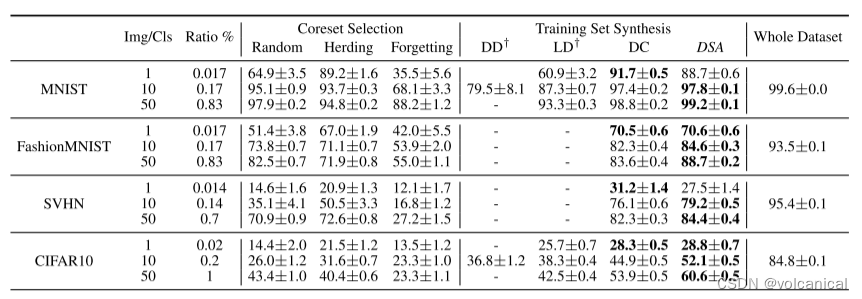
3. 实验结果