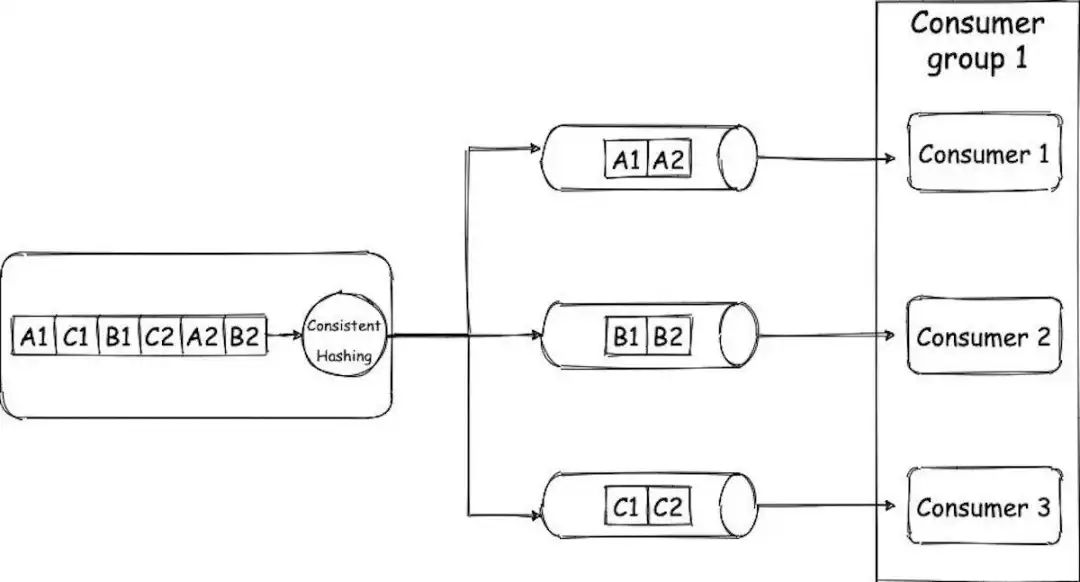
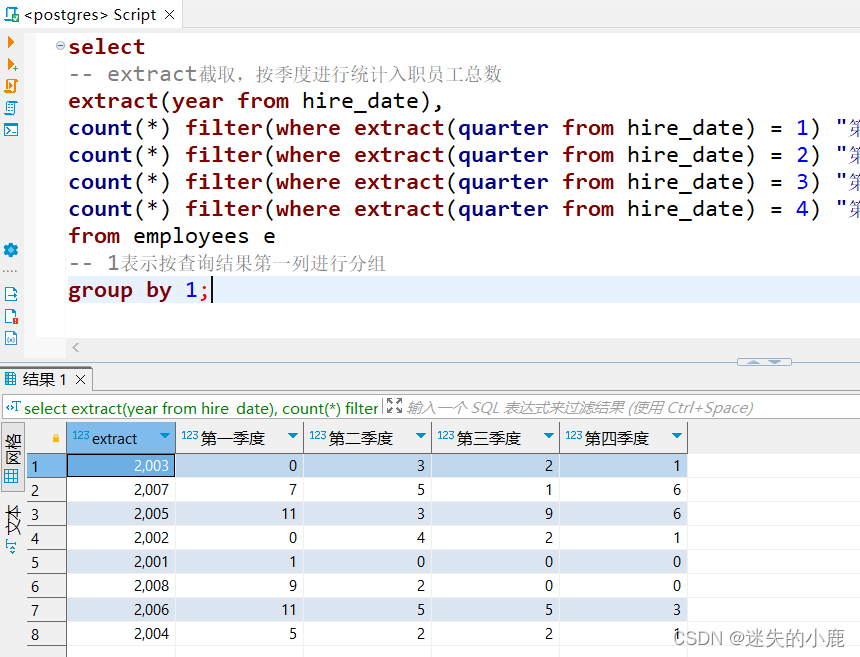
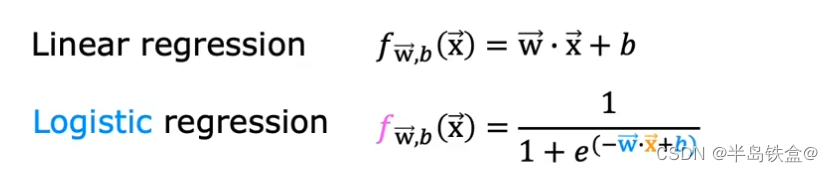0.什么是爆轰
其反应区前沿为一激波。反应区连同前驱激波称为爆轰波。爆轰波扫过后,反应区介质成为高温高压的爆轰产物。能够发生爆轰的系统可以是气相、液相、固相或气-液、气-固和液-固等混合相组成的系统。通常把液、固相的爆轰系统称为炸药。
19世纪80年代初,法国物理学家M.贝特洛、P.维埃耶、E.马拉尔和H•-L勒夏忒列等做过火焰传播实验。他们将一个充满可燃气体混合物的管子一端点燃,发现火焰通常以数厘米每秒到数米每秒的低速传播,但是在某些特殊情况下,这种缓慢的燃烧过程能够转变为高速的特殊燃烧过程,他们称这种现象为爆轰。后来发现,固相和液相炸药也能发生爆轰。
爆轰过程不仅是一个流体动力学过程,还包括复杂的化学反应动力学过程。两者互相影响、互相耜合。爆轰还伴随着热、光、电等效应。爆轰同周国介质相互作用时,周围介质中会产生激波或应力波,推动物体运动,造成物体破坏。人们通常把一种特定形式的燃烧——爆燃和爆轰联系起来考察。爆轰与爆燃最明显的区别在于传播速度不同,爆轰的反应区界面相对于介质以超声速传播,速度可达103~10-米/秒的量级,而燃烧则是依靠热传导和对流、扩散的方式使介质发生缓慢的化学反应,反应区界面相对于介质是亚声速的。爆轰中的化学反应过程高速释放能量。因此,爆轰的功率很大,高效炸药每平方厘米爆轰波阵面的功率高达1010瓦。这个特点使爆轰成为一种独特的能量转换方式。爆轰现象的研究通常包括爆轰的起爆、爆轰波的结构和爆轰同周围介质的相互作用等问题。
爆轰的起爆
通常应用火花放电或激波使气体混合物起爆,应用雷管和传爆药使药柱起爆。在起爆过程中,激波到爆轰的转变(简称SDT)和爆燃到爆轰的转变(简称DDT)这两个问题是爆轰研究中的重要课题。大量的研究表明起爆的过程有两类:①对于气相、液相(不含气泡和杂质)、固相(单晶)均匀系统,初始激波波阵面后的物质整体受热,发生化学反应,并在受热时间最长也即最早受到冲击处转为爆轰。爆轰波在已受到冲击的介质中传播,成为过压爆轰,此过压爆轰波赶上初始激波波阵面而发展成为定常爆轰。②对于液、固态不均匀系统,冲击起爆过程很复杂,初始激波同不均匀系统中的密度不连续处介质相互作用,形成热点,发生化学反应,放出能量加强初始激波,加强虽的激波同密度不连续处介质相互作用,形成温度更高的热点,使更多的炸药分解,放出更大的能量,这样激波不断得到加强,直接转入定常爆轰。
研究SDT和DDT时证实,起爆刺激赋予含能物质的能量密度和功率必须高于起爆阈值,起爆國值是随机变化的。但是,在20世纪下半叶,发现某些强度和功率显著低于起爆阈值的刺激偶尔也能起爆含能物质,称之为XDT,意为未知原因诱发低概率爆轰。虽然XDT概率很低,却对使用可靠性和安全性造成不可接受的威胁。现已查明,虽然低强度长脉冲赋予含能材料的平均能量密度和功率远低于其起爆阈值,但受力不均匀或物性分布不均匀导致沉积在含能物质中的能量分布不均匀,能量沉积局部化,在某种合适的环境里局部化区域的含能物质生成热点,并经历足够长时问演化达到起爆条件,诱发含能物质爆炸。由于需要冲击载荷、物性、环境三方面因素都满足局部化条件,所以XDT成为小概率事件。
爆轰波结构
爆轰波的结构是爆轰研究的主要问题。D.L.查普曼于1899年、E-儒盖于1905年分别提出最简单的爆轰波结构理论,后称为C-J理论。20世纪40年代,Y.B.泽利多维奇、小冯•诺伊曼和W.杜林各自独立地建立起了爆轰波内部结构的模型,后称为ZND模型。
•C-J理论
它把爆轰波简化为一个冲击压缩问断平面,其上的化学反应瞬时完成,在问断面两侧的初态、终态各参量可以用质量、动量和能量三个守恒定律联系起来,可得如下三个方程:

式中p为压强;v为比容(v=1/p,p为密度);e为比内能;u为质点速度;D为爆轰传播速度,即爆速;下标“0”表示初态。第二式在p一v平面内为一直线,称为瑞利线;第三式称为许贡纽方程,它是p一v平面内的一条曲线,称为许贡纽线(图1。一切同初态(Po,v0)满足守恒关系的状态点都在许贡纽线上。

爆轰产物的状态方程可写作:

四个方程中共有五个未知量,要单值确定爆轰参量,还须找出第五个方程。为此,查普曼和儒盖提出了著名的假设(称为C-J假设或C-J条件):稳定爆轰产物的状态对应于许贡组线和瑞利线的切点J,即C-J点(图1),该点的爆速D,是极小值,可以证明,在J点有下面关系:

式中c为声速;下标”了”为J点的值,爆速为常数。圈1曲线的BA段对应于爆轰过程,AE段不对应于任何实际过程,EF段对应于爆燃过程。爆轰波和爆燃波的一些性质见表1。

对实际爆轰系统应用C-J理论进行计算,一般都能得到同实验爆速值相近的结果,这表明C-J理论基本正确。但是,对气相爆轰进行精密测量得到的爆轰压强和密度值,比用C-J理论得到的值约低10%~15%,对爆轰产物实测得到的马赫数比计算的C-J值约高10%~15%。这表明C-J理论是一种近似理论。另外,炸药的爆轰实际上存在一个有一定宽度的反应区,而且有些反应区的宽度相当大,因此,将爆轰波仅仅看作一个强间断面己不恰当。这说明还须对爆轰波的内部结构进行深入研究。
爆轰波具有双层结构:前面一层是以超声速推进的激波,紧跟在后面的一层是化学反应区。激波仍作为一个强问断面,爆轰物质被瞬时地压缩到高温高密度状态,接着开始化学反应,直到反响。图2为ZND模型(下方为压强分布)。除初始物质、爆轰产物和 合物的状态方程外,还必须建立反应速率方程:

式中5为化学反应程度变量,称反应进度;t为时间;入为反应速率,它是压强刀、温度卫和女的函数。在ZND模型中,专=0对应手反应区的初态,即激波后的状态;§=1对应于反应区的终态。反应区内各点处于热力学平衡状态。在反应区内各点部分反应许贡纽线的方程式为

由瑞利线、许贡纽线和反应速率方程,原则上就能得出反应 区内各参量的空问分布或时间分布。

图2 爆轰的ZND模型和其中的压力分布(取随激波运动的坐标系)
ZND模型的爆速为常数,爆轰阵面是平面,流场定常,与C-J模型描写的爆轰同称理想爆轰。许多真实的爆轰的波阵面与流场不是一维平面的,与理想爆轰不一致,不满足C-J条件,称为非理想爆轰。20世纪50年代以来,虽然逐步发展了更接近实际的非理想爆轰理论,理想爆轰的C-J模型和ZND模型仍获广泛应用。
实验研究
1926年,C.坎贝尔和D.W:伍德黑德在研究气体混合物2C0+02的爆轰特性时,首先观察到爆轰波中有周期性扰动存在。爆轰波在圆管中传播时,如果在管内壁涂上一薄层银粉或烟炭,可以观察到螺旋线的痕迹,故称此种爆轰为螺旋爆轰。起初以为螺旋爆轰只是在接近可燃气体爆炸浓度极限时才出现的一种不稳定现象,但20世纪70~80年代的大量实验研究发现,螺旋爆轰是一个普遍存在的现象。接近化学当量比的可燃气体爆炸,用烟炱法均可见多头螺旋线痕迹,气体爆轰波阵面都具有复杂的三维结构。在扁平管中,可以观察到在烟炭层平面上具有很规则的胞格结构。在扩展的球形爆轰中也观察到类似的结构。用高速纹影照相、闪光干涉仪,在液体和固体炸药的爆轰中也发现了与气相爆轰相似的胞格结构。观祭到的胞格尺寸此正常燥轰反应区的宽度大一两个数量级。实验表明,除了沿爆轰波传播方向前进的波外,还有横向的弱激波在做周期性的脉动,横波的机制则正在探索中。图3为爆轰波阵面结构。
根据大量的实验研究结果认识到,爆轰波一般具有不定常、非平面和多波头的胞格结构。C-J状态只是一个宏观热力学的平均状态,它是大量微观或准微观状态的综合表现。尽管C-J假设不能反映复杂的爆轰波结构,仍不失为一较好的近似。

图3 爆轰波阵面结构示意图
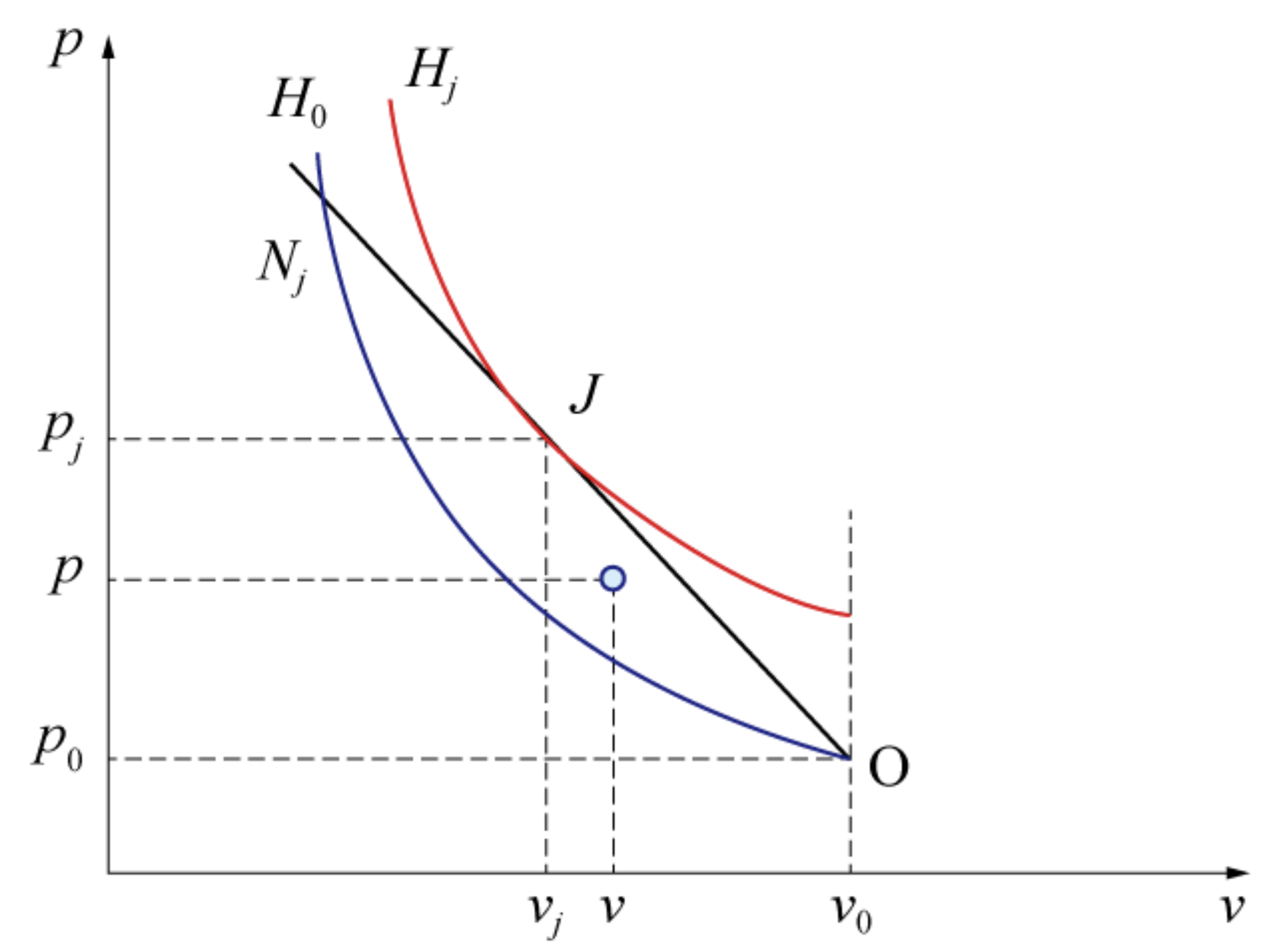
经过C-J点的许贡组曲线记作正j,未反应的许贡组曲线记作F0。在受限环境点燃炸药时,时常观察到不在五;曲线上的状态,其压力高于p,比容小于v0,传播速度低于音速。这正是常见的爆燃现象,它不稳定,既可能发展到爆轰,也可能燃烧殆尽或熄灭。如图4(p,0)点所示,这种爆燃状态在未反应许贡细曲线H0和瑞利线O Nj之间。
•同介质的相互作用
当爆轰波同周围介质相互作用时,在介质中产生激波或应力波,推动物体运动,造成层裂、破碎等。爆轰是一种高速的能量转换方式,也是产生动态超高压的一种手段,压力值可近10^2吉帕。图5为一些材料的冲击绝热线和炸药爆轰产物的反射许贡纽线。两者的交点决定平面爆轰波正冲击时在物料表面产生激波的初始强度。

如果爆轰波不是垂直而是倾斜作用于物料表面,即爆轰波滑移入射(图6),爆轰产物初始运动方向平行于物料表面,在物料中产生的激波强度要小得多。表2给出两种情况下B炸药冲击波压力的比较。

1.发动机的燃烧理论
几乎所有的喷气式发动机在燃烧室里的动作都是连续燃烧,稳定燃烧是常规喷气式发动机稳定工作的一个关键,但爆震发动机不一样,在燃烧室内的工作过程是爆轰波,也就是大家俗称的爆炸,而且是一次接着一次不断的爆炸,爆震发动机的名称就来源于此。
爆震燃烧过程有很高的燃烧速度和反应物转换速率,可近似为等容燃烧过程,这种燃烧过程的热循环效率远高于常规等压燃烧的超声速爆震燃烧的发动机。而常规的喷气式发动机燃烧室则是等压燃烧过程,燃烧时候压力增大时就会排气,形成自我调节的恒定压力,压力波传递以音速传递,当然你也可以理解为没达到最高压力时就漏气了,其效率显然受到了影响。
而等容燃烧则不一样,它在一定的空间内混合燃烧,其爆轰波传播速度高于音速,一般的混合气爆轰波可以轻易达到1400米/秒以上,在形成高压后向尾喷口扩散,完成一次排气动作,重新进入下一个循环,这种方式的燃烧过程可以是贫油燃烧,也就是混合气浓度很低,而等压燃烧需要比较高的混合气,因此等容燃烧非常节省燃料。
传统发动机理想布雷登循环包括等熵压缩、等压加热、等熵膨胀和等压放热四个过程。而传统燃烧室由于存在摩擦损失、扩张损失、加热损失、混合损失,一般存在4%~6%的压力损失。增压燃烧(pressure-gain combustion),顾名思义,即是在燃烧放热过程中同时增加燃烧室排气压力,而不是压力损失,从而提高发动机效率,降低油耗。
下图对比了等压燃烧、等容燃烧和爆震燃烧三种不同热力循环,三种燃烧热力循环下的发动机热释放增加量是相同的。
但是,不同热力循环导致涡轮进口的气流总压不一致,其中等容燃烧和爆震燃烧热力循环涡轮进口总压较高,能够提高燃气涡轮发动机总体性能,相对于传统发动机热力循环过程(等压燃烧),发动机熵增减小,输出功增加。在燃烧相同燃料情况下,可以获得与等压燃烧基本相同的温升、更高的压力,从而产生更高的热效率。

就目前技术发展来看,增压燃烧技术主要包括以下四类:
脉冲共振燃烧(Resonant Pulse Combustion)、脉冲爆震燃烧(Pulsed Detonation Combustion)、旋转爆震燃烧(Rotating Detonation Combustion)以及内燃波转子(Internal Combustion Wave Rotor)
而等容燃烧则不一样,它在一定的空间内混合燃烧,其爆轰波传播速度高于音速,一般的混合气爆轰波可以轻易达到1400米/秒以上,在形成高压后向尾喷口扩散,完成一次排气动作,重新进入下一个循环,这种方式的燃烧过程可以是贫油燃烧,也就是混合气浓度很低,而等压燃烧需要比较高的混合气,因此等容燃烧非常节省燃料。

另一个则是超燃冲压发动机内部的燃烧过程也有些类似于等容燃烧,与爆震发动机一样,都比较适合在高超音速下工作,不过超燃冲压发动机需要由其他发动机将其加速到音速的4倍以上才能启动!

而爆震发动机却不是这样!因为其工作范围非常宽,可以零速度启动、并且单位燃料消耗率低,结构与冲压发动机不一样但同样非常简单,爆震发动机简单到极致的甚至只有一根管子,不过爆震发动机的种类不一样,各项应用前景差异也非常大,目前比较主流的爆震发动机有如下类型:
脉冲爆震发动机(PDE);
旋转爆震发动机(RDE);
斜爆震发动机(ODE);
2.爆轰发动机原理
最简单的爆震发动机就是单管式PDE,这种发动机在短视频平台上很多,就一根长管子,前部是一个进气结构+爆轰燃烧室,后半部分就是一根长管子,工作的时候整根管子都烧红了,场面很是壮观。

这种结构可以用固定式的结构来实现,只是频率不太好控制,比较随性了!当然也可以用部分旋转部件来实现,提高总推力的话还可以用多管并联,形成一个PDE爆轰阵列,就是得协调下多管爆震之间的频率,不要形成共振,一般单管频率能达到60HZ以上就可以认为大致连续了,假如能达到100HZ以上,那基本就是连续了。

除了多管并联以外,还可以和涡喷或者涡轮风扇发动机结合,在外涵道上组成一个PDE环形阵列,提高发动机推重比,PDE对燃料不太敏感,可以用气相燃料,也可以用液相燃料,甚至还可以与火箭发动机结合,形成大气层内PDE,大气层外火箭这种空天飞机的发动机结构。

旋转爆震发动机(RDE)
PDE结构需要多次点火,需要高频率起爆,而另一种环形燃烧室结构的旋转爆震结构(RDE避免了这种问题,它的基本概念是形成一个环形通道,燃料和氧化剂通常通过小孔或狭缝注入通道,一次启动后会形成一个或多个爆震波,在燃烧室头部旋转传播,燃烧产物从另一端高速排出产生推力。

它的比脉冲爆震(PDE)要更稳定,其爆轰波同样是超音速扩展,保持了PDE的优点,避免了PDE的缺点,旋转爆震发动机是目前全球多国突破的方向之一。
斜爆震发动机(ODE)
斜爆震方式看着结构更简单,但稳定爆震技术难度很大,因为斜激波的起爆和激波、爆震波的驻定(维持在特定位置和角度)都非常依赖于高超音速的条件,在三种典型的爆震发动机结构中,斜爆震难度是最高的:
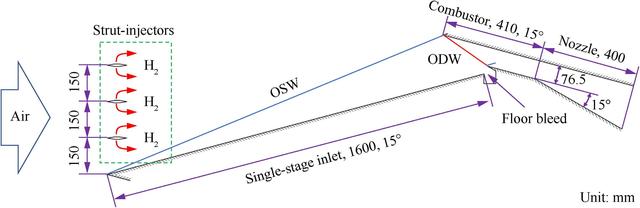
斜激波爆轰结构示意图
斜激波爆震结构利用一道或者多道斜激波对气流进行压缩,激波后的流动混合作用把燃料和空气混合均匀,在下一道激波产生的高温高压正好点燃,然后在燃烧室的一个极薄锋面上发生爆震,爆轰波超音速传递扩散形成推力,这个要求实在是太高了!
但斜激波爆震理论上可以达到16马赫以上,这比超燃冲压发动机的6~10马赫要高出不少,诱惑力非常大!自提出这个概念以来国际上多个组织曾展开大量研究,但一直很难达到稳定工作,而且其门槛极高,需要高超音速风洞,显然这就是劝退!
实验是在标称马赫数9的速度下进行的,观察到站在燃烧器中的倾斜爆轰保持稳定状态长达 50 毫秒。可以在燃烧室中清楚地看到存在斜向爆震驻波,氢气在先导激波后面很短的距离内燃烧殆尽,与倾斜冲击波耦合在了一起。

Sodramjet 发动机概念演示模型及其在 JF-12 激波风洞中的安装
直立斜爆轰前沿由过渡区和充分发展爆轰两部分组成,过渡区是从斜激波的起源点到反应锋追上斜激波的位置,试验证实了Sodramjet发动机可以实现,倾斜爆震发动机的概念已经提出了数十年,但首次在风洞中成功演示。

白热的激波层,这是诱燃和起爆的关键
从以上几款典型的爆震发动机可以看出,我国在最先进的旋转爆震以及斜激波爆轰发动机中均处在前列,看来未来的高超音速飞行器上要用爆震发动机了。
3.连续爆轰发动机数学建模
脉冲爆震发动机通常由进气装置、爆震室、尾喷管、推力
器、爆震起爆及频率控制系统、燃料供给和喷射系统及控制 系统组成。从爆震室前段(封闭端)喷入燃料,与从进气装置 进入的空混合形成可爆混气,通过靠近爆震室后端的各单个 “爆震管”激发产生爆震波。根据爆震室的进气方式不同可 分为:阀式和无阀式脉冲爆震发动机。阀式脉冲爆震发动机 利用阀的机制来进气和隔离气体,使发的工作、燃料的喷射 和混气的点火正时。无阀式脉冲保证怎发动机让气体连续 流过整个发动机,调节燃料的喷射和混气的点火的正时。无 阀式脉冲爆震发动机的工作循环过程主要包括:1 充填隔 离气体,同时扫除上循环的燃气;2 充填可爆燃气;3 点火 起爆;4 爆燃转向爆震,爆震波向敞口端传播;5 膨胀波进 入爆震室;6 膨胀排气结束。具体如下图所示。

脉冲爆震发动机是利用间歇式或脉冲式爆震波产生的 高温、高压燃气来产生推力的一种新概念发动机。因此,脉 冲爆震发动机的性能特点在很大程度上是由爆震波的特性所决定的。爆震是一种具有比爆燃能量更高和猛烈的燃烧 现象,以超声速传播的爆震波,与一般喷气发动机中使用的 以亚声速传播的爆燃波不同,它能产生高温(高于 2 0 0 0 °C ) 、 高 压 ( 大 于 1 0 ~ 1 0 0 a tm ) 、 高 速 燃 烧 与 释 热 ( M > 4)的 燃 气 。 同 时 ,由 于 爆 震 波 传 播 的 高 速 特 点 ,其 燃 烧 过 程 可看作是等容燃烧过程,因此热效率高。据此,脉冲爆震发 动机具有如下性能特点:
1)脉冲爆震发动机的推重比高(大于 20),单位体积的 发动机推力大。由于爆震波能产生高温、高压气体,因此,就 不需要像在传统的涡喷发动机中的那样用压气机来压缩空 气以提高压力,所以脉冲爆震发动机不需要压气机,自然也 就不需要涡轮,而且供燃料时燃烧室内仍为低压,故也不用 涡轮泵。由于没有高速旋转部件,在同样的推力下,脉冲爆 震发动机比火箭与冲压发动机还要轻,比涡喷发动机更轻, 而且结构简单,制造成本也低得多。
2)循环热效率高,燃料消耗率低,而且比冲高。由于脉 冲爆震发动机的工作循环为等容循环,因此,循环热效率高, 燃料消耗率低。如在压比为 6时,等容循环的热效率比等容 循环的热效率高30% ~50%。假定在同样的推进效率下,在发动机中用爆震反应代替爆燃过程,能降低燃料消耗率 30% ~50%。脉冲爆震发动机的比冲可大于 20s,而脉动喷气发动机虽然省燃料,但热效率低,比冲不高。 3)工作范围宽广,且推力可调。脉冲爆震发动机可在 M0=0~10,H=0~(30~50)km的飞行范围内工作,且推力 可调。由于它能在宽广的速度、高度范围内工作,所以脉冲爆震发动机是组合式推进系统的理想候选者。 4)熵增低。以天然气为例,爆震等容燃烧的熵增比爆 燃等容燃烧(脉动燃烧)低 9%,比等压燃烧低 35%。熵增低 意味着不可逆过程的做功能力大,使得接近等容的燃烧过程有较高的热力学效率。

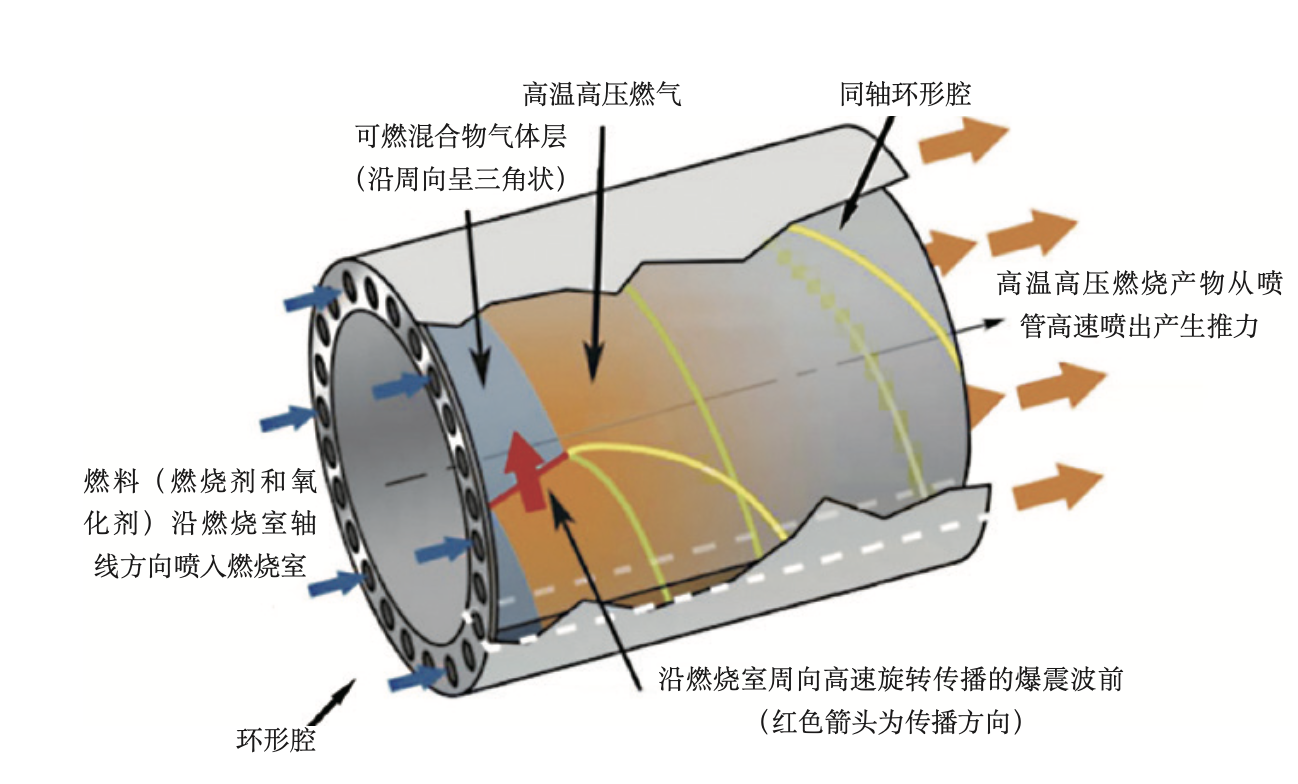
旋转爆震包括以下步骤:用燃料和氧化剂填充环形爆震管的某一角向位置,点燃混合物,朝向管的周向以超音速传播爆震波,以及排出燃烧产物。下一时刻,则在环形爆震管的下一角向位置填充燃料和氧化剂,形成下一个爆震波,以此循环。其优点是不需要持续脉冲点火源,一次点燃,持续燃烧。可以以非常高的频率运行,一般为kHz,产生连续的动力输出。氧化剂入口采用气动阀控制,以减少和防止回流和回压。

旋转爆震发动机(RDE)的推力是连续的。蓝色为未燃的预混合气体,红蓝界面是爆震波位置,蓝线是爆震波沿管壁的运动轨迹,绿线是爆震产生的激波在管壁上的轨迹,管内红色由深变浅显示温度逐渐降低和压力释放的过程,每一个圆孔都是“进气口”,所有进气口同时工作,各自形成爆震波


左为另一个视角,右为沿圆周展开后其中一个爆震波和激波的分布

RDE是环管结构,爆震波在环管内回旋扩散,这样的三维爆震波的形成和扩散不是光有理论就能解决的,需要复杂、昂贵的实验来验证。
斜爆震发动机(简称ODE),也称驻定斜爆震冲压发动机(简称SODRAMJET)或者斜爆震波发动机(简称ODWE)。ODE利用一道或者多道斜激波对气流进行压缩,激波后的流动混合作用正好把燃料和空气混合均匀,下一道激波的高温高压正好点燃,然后在稍后的一个极薄锋面上产生爆震,形成推力。为了改善和在更大范围内可靠诱燃和起爆,也有用激光、热射流、磁流体点燃的。

ODE结构十分简单,设计十分复杂。

4.爆轰数值计算
在爆轰波的理论计算方面,最早在 20 世纪初由英国物理化学家 Chapman 和 法国工程师 Jougurt 分别建立了预测爆轰波速的理论计算模型,后称“C-J”理论。 该理论忽略爆轰波的内部结构,认为化学反应具有无限快的速率,同时假设爆轰 波后气流速度达到声速,从而求解出爆轰波后压力、温度等气流参数。二战期间 Zeldovich、von Neumann,Doring 引入了化学动力学过程,将爆轰波描述为由前 导激波、诱导区和化学反应区构成的有限厚度的薄层,该理论称为“ZND”理论, 所建立的爆轰波结构又称“ZND”结构。ZND 结构是被认为较为接近真实的爆 轰波结构,得到了很好的实验验证。
随着计算机和数值计算技术的发展,国内外学者提出并发展了大量基于 C-J 理论和 ZND 理论的爆轰波计算方法,常用的有三种。第一种基于 C-J 理论,认 为化学反应速率无限大,放热在瞬间完成,且反应前后比热比是已知的。该方法 人为假设反应放热量和化学反应前后的气体性质,作为定量研究的方法不够准确, 但能够定性研究爆轰波的许多性质,且对 C-J 爆速的预测是比较准确的。第二种 方法考虑了爆轰波化学反应面与激波面的强耦合特性,假设无限快反应速率,建 立了化学平衡激波关系,在求解气相爆轰波方面有很可观的计算速度和准确性。 第三种方法则考虑了更加真实的化学反应动力学过程,即求解具有化学反应源项 的 N-S 方程组,属于计算流体力学(CFD)方法,该方法最贴近实际的物理化学 过程,但计算速度相对最低。
CJ 理论以热力学以及流体力学理论为基础,假设爆震波是一个伴随放热的强间断面; 爆震波面平整,跨过爆震波面的流动是平面一维的,不考虑摩擦、传热等耗散效应;化学反 应速度极快,跨过爆震波化学反应瞬间完成并释放反应热;以爆震波为参考系时爆震波传播 是定常流动,波前波后流动参数不随时间变化。考虑爆震波以波速 D 传播时,波前状态采 用下标“0”表示,波后参数采用下标“1”表示,则采用以上假设,将坐标系固连在爆震波 上时,描述爆震波前后流动状态的方程为

在波前反应物处于静止状态时,通过式 0.1 与 0.2,并将 x = v0/v1,y = p1/p0 代入,其中 v = 1/ρ,可得

声速公式为

将声速公式(0.5)代入公式(0.4),并考虑马赫数 M0 = D/a0,整理得

在 p-v 图上,(0.6)表示 Rayleigh 线,表示激波后状态的可能集合。
根据式(0.1)与(0.2)可得
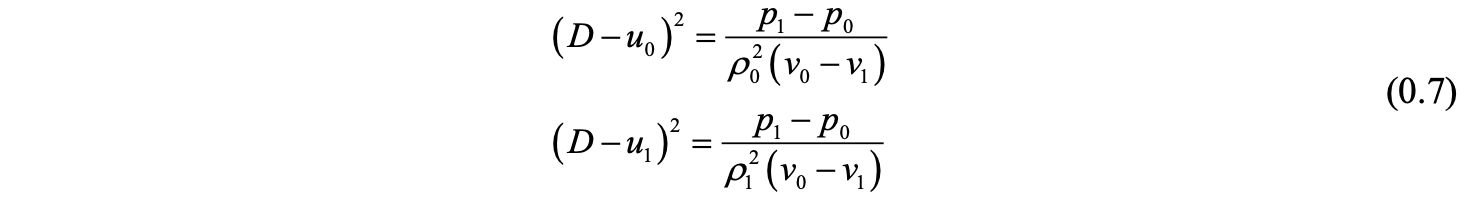
将(0.7)式代入式(0.3),并将焓分解为与温度有关的显焓以及与无关的生成焓,整理可得

其中,h0 与 h1 分别表示爆震波前后气体显焓,q 表示放出的热量,其数值等于反应物与产物 的生成焓之差,具体形式分别为


其中,xi,r 与 xi,p 分别表示反应物与产物中第 i 个组分的摩尔分数。令 q’ = q/p0v0,并假设爆震波前后气体为理想气体,则其状态方程为

将(0.11)式代入(0.8)式并整理成 x 与 y 的形式

其中,α、β 的具体表达为

式 (0.12)则是表达激波前后状态关系的 Hugoniot 曲线。事实上,产物各组分质量分数以及 放出的热量是未知的,但假设 CJ 状态时产物处于化学平衡状态即可采用最小自由能法迭代 求出相应的组分质量分数以及释放的热量,本文如无特别说明,均采用 Cantera 结合 SDToolbox[]计算相应的 CJ 爆震参数。
由方程(0.1)-(0.3)、(0.11)可知,方程中含有 ρ1,p1,q,D,u1 五个未知数,而方程只有四个, 方程的解是不确定的,表现在图 0.1(a)上则是方程可能有 1 个根,两个根或者无根,因此, 为获得方程的唯一解,Chapman 和 Jouguet 分别提出了封闭以上方程组的条件。Chapman 根 据 Rayleigh 线与 Hugoniot 线相交的关系,发现当 Rayleigh 线斜率小于某个特定值时,Rayleigh 线与 Hugoniot 线无交点,此时方程无解,如图 0.1(a)中 U<UCJ 情形;增加斜率,Rayleigh 线 将与 Hugoniot 线相切进一步相交,分别对应方程存在一个解和两个解,如图 0.1(a)中 U=UCJ 与 U>UCJ 的情形。Chapman 从实验角度出发,对于给定的爆炸混合物,当触发爆震行为时, 爆震波将以一个特定的速度传播,因此,他认为爆震波稳定传播的速度为 Rayleigh 线与 Hugoniot 线相切对应的速度。

图 4.1 氢气与空气混合物在 p0=1bar,T0=300K 条件下爆震分支的 p-v 图
Jouguet 详细考察了不同爆震波速的 Hugoniot 线曲率,并分析了熵参数随 Hugoniot 线变 化的趋势,他认为爆震波稳定传播时的速度对应 Hugoniot 线上熵最小的点,如图 4.1(b)上的 等熵线 S3 所示,进一步分析表明熵值最小点处的粒子速度与当地声速相等。在随后的研究 中发现,Chapman 提出的最小速度准则与 Jouguet 的熵最小判据以及声速面判据是等价的, 如图 4.1(b)所示。因此,将 Chapman 与 Jouguet 提出的封闭方程组的条件称为 CJ 准则或 CJ理论。 根据热力学关系式得到

去掉(0.8)式下标“1”,并对两端取微分得到

将式(0.14)代入式(0.15)可得

在 CJ 点处,Rayleigh 线与 Hugoniot 线相切,二者斜率相等,上式右端为零,因此

式(0.17)表明熵沿着 Hugoniot 线变化时,在 CJ 点处取得极值。由图 4.1(b)可知,在 CJ 点之 下,即 v>vCJ 时,Rayleigh 线斜率小于 Hugoniot 线斜率,因此熵沿着 Hugoniot 线上比容增大 而增大;而在 CJ 点之上,即 v<vCJ 时,Rayleigh 线斜率大于 Hugoniot 线斜率,因此熵沿着 Hugoniot 线上比容增大而减小;因此,在 Rayleigh 线与 Hugoniot 线相切的 CJ 点,熵具有最 小值。穿过 CJ 点的等熵线的斜率与 Rayleigh 线相切,在 CJ 点处有

因此有 D-u=af,即 CJ 点处质点速度与当地声速相等。综合(0.15)-(0.17)可知,最小速度、熵最小以及声速面三者等价。
ZND 模型
采用 CJ 理论计算的爆震速度与实验结果十分吻合,但 CJ 理论只考虑爆震波两侧流体
状态,忽略了爆震波反应区厚度以及具体的反应路径,因此,不能对反应物的可爆性进行评 估。Zel’dovich、von Neumann 以及 Doring 认为爆震波是由一道前导激波及紧跟其后的反应 区组成,前导激波绝热压缩反应物使其反应并释放大量能量,跨过反应区,压力以及密度具 有一定程度的降低,而气体粒子受热后膨胀加远离激波面,为满足动量守恒,必将产生额外 的力推动前导激波往前传播,当气体粒子速度加速至声速时,反应终止,该截面称为广义 CJ 面,而该一维模型也称为爆震波的层流模型或 ZND 结构。相比 CJ 理论而言,ZND 模型 给出了爆震波的具体结构及自持传播机制,能够在一定程度上对反应物可爆性进行分析。
为研究方便,基于激波坐标系的控制方程组可写为[]

方程组(0.14)从激波后状态开始积分,直至积分面满足奇异条件,即 时,积分所得的状态参数以及组分质量分数变化过程即为一维爆震波 ZND 结构,也称为本 征爆震,典型的计算结果如图 4. 2 所示。

图 4. 2 当量比为 1 的 H2-Air 混合物在 p0=1 bar,T0=300 K 时平面爆震的 ZND 结构
激波化学平衡方法
激波化学平衡方法的建立 一般认为,在激波波阵面紧后方不能瞬时达到化学热力学平衡状态,在波阵
面后存在一定的弛豫过程。但我们前面已经谈到,爆轰波化学反应面与激波面之 间具有的强耦合的特性,宏观上来看,爆轰波内非平衡弛豫过程形成的内部结构 相对流动尺度可以忽略不计。这与高超声速绕流的反应激波存在区别,高超声速 流动中激波诱导的化学反应(如空气的解离)具有较长的诱导距离,接近流动本 身的尺度,其弛豫过程不能够被简单地忽视。
正是由于爆轰波的存在的反应面和激波面强耦合特性,假设了无限快反应速 率,把爆轰波处理成间断面的 C-J 理论能够在爆轰波宏观行为的预测上取得成功, 而化学平衡激波关系则是在 C-J 理论上的进一步改造。

图 5 多组分气体化学平衡激波关系示意图
如图 5 为多组分气体化学平衡激波关系示意图,不同于 C-J 理论,化学平 衡激波关系中不假设反应前后比热比γ、放热量 q 是已知量,而只需要假设来流 速度 u1、压力 p1、密度ρ1、温度 T1(或焓 h(T1))以及激波前的气体成分(图中
为摩尔分数 Xi1)是已知的。然后,根据波前的物理量求解波后的速度 u2、压力 p2、密度ρ2、温度 T2 以及气体组分 Xi2。当上述物理量满足激波关系,且激波后 的气体组分 Xi2 满足波后当地压强ρ2、温度 T2 下的化学平衡关系,就形成了化学 平衡激波。
因此,化学平衡激波关系可以被分为激波关系与反应平衡两部分迭代求解 [7],在计算激波关系时,我们需要假设波后组分是已知的,利用波前的流动参 数和激波前后的组分求解出波后的流动参数;计算化学平衡时,根据波后的压力、 温度计算出波后组分的平衡状态。当算出了波后的平衡组分后,再次计算激波关 系式,不断迭代直至收敛,其逻辑框图如图 6 所示。
该化学平衡激波求解迭代方法具有类似爆轰波 ZND 结构假设的物理意义:
ZND 结构中,爆轰波的反应区可以被认为是爆轰波的一个中间解,产物区流动 是爆轰波的化学平衡解。化学激波平衡算法的迭代路径则可以模拟该 ZND 结构 中的化学动力学反应过程:迭代开始时假设激波前后冻结无反应,类似 ZND 结 构的 von Neumann 面,迭代过程中组分逐渐收敛至平衡状态,且温度随迭代过 程逐步上升、压强下降,变化规律与 ZND 结构的反应区相同。张子健在提出该 方法的基础上,证明了算法的物理意义,可参考文献[7]、[8]。需要简单指出的 是,经作者实践后发现迭代过程中物理量的变化规律并不一定与 ZND 结构相似, 这受迭代初值和松弛因子的影响。

图 6 化学平衡激波求解流程
激波关系求解
考虑积分形式的一维定常流动控制方程:

上式中焓值为比焓。此外,还需要理想气体状态方程封 闭方程组:

注意到比焓和比热都是温度的非线性函数,由式(1-3-13)~(1-3-17)确定,因 此上式无法求得解析解。方程的迭代求解主要在于(2-1-3)中非线性函数 h(T)的处 理上,据此我们考虑一种针对温度 T 的牛顿迭代方法:
将式(2-1-2)除以式(2-1-1),并代入式(2-1-4),得到:

整理得到用 u2 表达的 T2:

上式(2-1-3)联立,能唯一确定 u2 和 T2 两个变量。(2-1-3)将(2-1-6)代入中:

原方程组的求解转化为求函数 f(u2)零点的问题,采用牛顿迭代法,构造迭代 函数:

上式中,u2,k 是第 k 次的迭代值。f′ (u2)是 f(u2)对 u2 的导数,具体形式为:

上式中 cp2(T2) = dh2/dT2 是波后混合物的定压比热,它需要指定波后气体组分 并通过式(1-3-21)进行计算。对于冻结激波而言,则应当采用波前组分计算。
化学平衡组分的求解
本文化学平衡组分的求解与文献[7]相同,采用 NASA Gibbs 自由能最小化方法[9]。给定压力 Pa 和温度 T,混合气吉布斯自由能为:
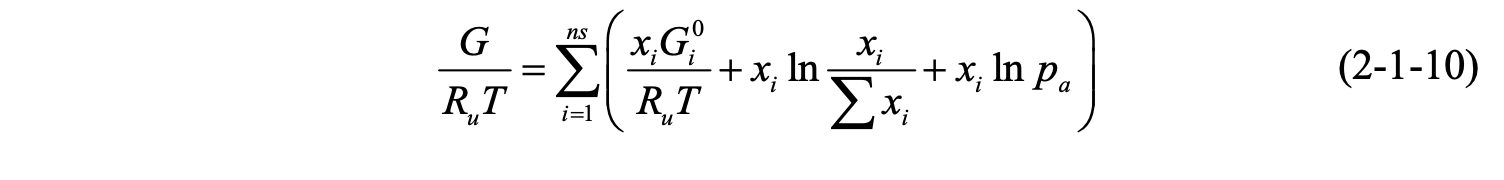
式中,xi 为组分 i (i = 1...ns)的摩尔数,尤其需要注意 pa 的单位为 atm。标 准摩尔吉布斯自由能 Gi0 根据式(1-3-16)计算,当混合气体处于化学平衡态时, G/RuT 取最小值。这是一个多元函数条件极值问题,其约束条件为元素守恒:

式中,bj 为元素 j 的总摩尔数,由反应物的组成给出;系数 aij 为组分 i 的分 子式中含元素 j 的原子个数;ne 为混合气体中元素的个数。作者建议在编程时
创建一个元素矩阵,比如,对于 H2O-O2 气混合气

,这样在后 续计算时较为方便。
为求解式()在的条件()下的极值问题,引入 ne 个拉格朗日乘子 λj (j =1...ne),并定义函数 F 为

关于组分摩尔 xi 和拉格朗日乘子λj 的多元函数无条件极值问题,当函数 F 对组分摩尔数 xi 的各偏导数∂F/∂xi 均为零时,函数达到极值,即:

采用迭代方法求解式(2-1-13)所示的非线性方程组的解 xi。给定迭代初值 yi 为 xi 的一个估计值,则偏导数∂F/∂xi 在 xi 处的值可用 yi 附近的一阶泰勒展开式 估计,即:

为求函数 F 的极小值,令式(2-1-14)中∂F/∂xi = 0,得到:

等式左端的 xi 就是经历一次迭代后新的平衡组分的估计值。等式右端的∑xi/∑yi 和λj 为以下线性方程组的解:

上式中第一式可通过对式(2-1-15)进行求和得到,而第二式可通过将式 (2-1-15)代入式(2-1-11)得到。该式看起来非常不清晰,我们将它写成矩阵形式, 以某两种元素构成 i 种组分的混合气为例,式(2-1-16)表示为:

这就清晰多了。需要注意的是,线性方程组(2-1-16)的系数矩阵容易是病态
的,求解时需要采取预条件处理的方法。 事实上,该迭代方法几乎不能直接求解,这个迭代过程是非常不稳定的,受
初值 yi 影响非常大,Gibbs 自由能往往不难随迭代过程逐步减小,且元素守恒条 件会被破坏,还容易出现所得组分摩尔分数 xi < 0 的解(这在数学上是允许的)。 因此,我们考虑一种松弛迭代的方法[10]:
令 zi = yi +φ(xi− yi)作为松弛处理后的新的计算值替代 yi,在每一步的迭代中 采取一下处理:
(1) 减幅因子φ
选取一个φ,使得每一步迭代达到以下目的:1. 新的的计算值 zi 满足元素守 恒的约束条件;2. 满足 F(zi) < F(yi),使每一步迭代确实是向自由能减小的方向 进行;3. zi > 0。
设置一个误差值ε1,令

这首先保证了 zi > 0,但无法保证吉布斯自由能下降的条件。为此,需要计算出zi = yi +φ(xi− yi)的值,并将代入自由能公式(2-1-10),进行迭代计算:

如果φ满足 F(zi) < F(yi)的条件,则当前的 zi 计算成功。否则,使 k=1, 2 ..., 直到 F(zi) < F(yi)为止。
(2) xi 近零值的处理
从式 zi = yi +φ(xi− yi)容易看出,当某一 xi 的真值为零或非常接近 0 时,为了 保证 zi > 0,φ将变得很小,这使得其它组分的迭代将陷入停滞,这是我们不能接 受的。为此,设定一个误差值ε2,对于

的组分,将不参与的选取,令其对应的φi=1,同时令该 xi = ε3。假设迭代方法求解 Gibbs 自由能的残差精度设置为ε,则当

时,能够实现迭代过程的稳定进行。其计算逻辑如图 8 所示。
C-J 爆轰速度的求解
采用激波化学平衡方法可以计算出更加真实的 C-J 爆轰速度,考虑到 C-J 爆轰的波后声速条件:

整理式(1-1-1)~(1-1-4),消去 u、ρ,得到方程:

上式不包含放热量 q,因为这里的 h 是比焓。p1、T1、R1、h1 是已知的,R2 和 h2都与波后气体组分有关,而波后气体组分则与 p2、T2 有关。因此,求解 C-J 爆轰 速度的问题被转化为求解 p-T 平面上满足守恒方程(2-1-20)、声速关系(2-1-19)和 化学平衡关系的解点(p2、T2)问题。为了找到这样一个解点,本文改进了一种逐 次逼近的方法[11]:
拆分式(2-1-20)的左右两端


图 7 化学平衡计算流程 计算开始时,我们假定一个初值 p2、T2(以及组分含量 Xi2)。首先固定压强
p2,通过对温度和化学平衡关系进行迭代,求 U1−U2 = 0 的零点,这样可以得到 一个满足方程(2-1-20)的温度T2*和组分 Xi2*。该过程称为温度 T 的逼近,其计算 逻辑如图 8 所示。
图中温度的逼近过程采用二分法,收敛过程利用了 U1、U2 的物理性质:在 平衡温度和平衡组分附近 U1−U2 是单调的,当 U1−U2 > 0 时,当前计算的温度 T2(k)偏高于平衡温度 T2*,需要降低 T2(k)重新计算,反之则需要升高。因此,人为 设定初始温度区间 Tmax (0) 、Tmin(0),通过二分法的方式可以使得区间逐步逼近当 前压力 p2* =p2 和平衡温度 T2*。经检验,指定 Tmax (0)=5000,Tmin(0) =1000 时可满 足绝大多数气相爆轰的计算要求。

图 8 温度逼近的二分法计算流程
注意到计算 p2*下的平衡温度 T2*时我们没有考虑 C-J 爆轰声速关系式(2-1-19),因此需要检验 p2*是否满足该关系式。

得到压强关系:

之间的大小关系,如果不满足所设定的计算误差,令下一次迭代的压强:

并重复上述温度逼近过程和压强计算过程,直至收敛为止。上式中为φ收敛因子, 经检验,指定φ=0.4 时有较好的收敛效果。
上述基于化学平衡关系求解 C-J 爆轰速度的迭代计算流程如图 9 所示。关 于该方法计算收敛性质的讨论可参考文献[11]
关于迭代初值的 p2、T2、Xi2 的指定问题,本文提供一种较为简单的方案: 首先人为假设一个 C-J 爆轰速度 u,可以取得稍微大一些。令 Xi2 = Xi1,通过 2.1.1激波关系求解方法计算在 p1、T1、u 下的冻结激波关系,得到的波后压强 p2、温 度 T2 作为迭代初值。

图 9 C-J 爆轰速度的迭代计算流程
5.爆轰发动机产研进展
军用场景
斜爆震发动机最终会用于高超音速飞机和空天飞机,极大地缩短世界上任何两地之间的距离,同时军事应用也是显而易见的。在短期内,最可能的应用是高超音速无人侦察机,无侦-8采用火箭动力达到了初步要求,但是有缺憾的。采用超燃冲压或者斜爆震发动机可以大大增加续航时间,增加侦察范围,达到“大气层内无限变轨卫星”的作用。
要是无侦-8能用上斜爆震发动机,航程和使用灵活性就是另一个境界了。“嫦娥5”返回时,采用水漂技术,这在探月和轨道航天器中是首创的。“阿波罗”和“联盟”飞船都是弹道式再入,用降落伞着陆。航天飞机是简单滑翔再入,以便水平着陆。“嫦娥5”依然是降落伞着陆,但采用水漂技术,或许是为了在水漂中降低再入速度,并更加精确地控制着陆点。不管是出于什么原因,中国对水漂技术已经玩熟了,不管是不是绝对必要,都可以玩一把,反正风险已经足够低。在这种情况下,空天飞机或者军事航天器可以在水漂中用斜爆震发动机加一把速就有特殊意义了,可以长时间无限制变轨,比现有的侦察卫星有用多了。前一段时间神秘的“中国X37”的意义似乎清晰了一点。
用于高超音速洲际导弹的话,可以用小得多的助推火箭升空,然后在亚轨道高空转入水平飞行。不仅弹道更飘忽,还因为助推火箭的尾焰比洲际弹道导弹小得多,与战术弹道导弹的尾焰特征相似,而增加判别困难。如果用包括斜爆震的组合发动机起飞,那就像飞机一样,基本无法用红外预警卫星预警了,将彻底打破美国的反导弹体系。而且速度达到M15-16的话,差不多达到M25一级的洲际弹道导弹速度的2/3,比不超过M8的超燃冲压导弹快了一倍,M2-3一级的超音速巡航导弹就根本不可比了。
高超音速导弹达到洲际射程的战略意义更是不言而喻。说到火箭,爆震发动机(不管是脉冲爆震、回旋爆震还是斜爆震)也是可以用于火箭发动机的,与大气层内使用相比,空气进气改成氧化剂进气而已。不过斜爆震需要进气就是超音速的,比较起来,脉冲爆震或者回旋爆震的火箭发动机可能更易实现一点。现有火箭发动机实际上还是等压燃烧,爆震的压力和比冲更高,用于火箭发动机可以把比冲至少提高30%。
RDE给炮弹增程是另一个可能的应用,用冲压发动机增程的炮弹已经实用化,RDE适应的速度范围更大,推进效率更高。爆震发动机另一个有意思的应用是炮弹增程。RDE比较容易与炮弹的形状相整合,由于只需要携带燃料,不需要携带氧化剂,与火箭增程相比,可以增加射程,或者增加装药。
至于斜爆震发动机与超燃冲压哪个更先进的问题,应该说各有优点,互相补充。等容燃烧的内燃机取代了等压燃烧的蒸汽机,但等压燃烧的燃气轮机重回江山了,所以不是等容燃烧必定比等压燃烧更先进那么简单。另一方面,等容燃烧的PDE和RDE或许有朝一日会补充等压燃烧的燃气轮机,在航空世界里各霸江山,而结合爆震燃烧的超燃冲压也在研究中。
连续爆震发动机在未来超声速客机的应用前景
相比于军用飞机和航天器,亚声速民机对于经济性、安全性和环保性更加重视。长期以来,民用发动机的改进都更着重于增加可靠性和降低油耗,而连续爆震发动机有熵增较小、热效率和比冲高的特点,在民航领域也具有相当的应用前景。
民航发动机提高经济性的措施主要包括增加压气机的压缩比、加大涵道比和提高涡轮前温度等。其中,对传统的涡扇发动机而言,涵道比增加到10 : 1左右已是极限,采用齿轮传动技术的涡扇发动机的涵道比可以增加至15 : 1以上,但也不能无限制增大;在增加压缩比方面,目前罗罗公司最新的“超扇”(UltraFan)发动机已达到了70 : 1的压缩比,但高压缩比也对压气机的设计带来了很大的挑战;至于涡轮前温度,也已经达到了目前材料科学所能承受的极限。
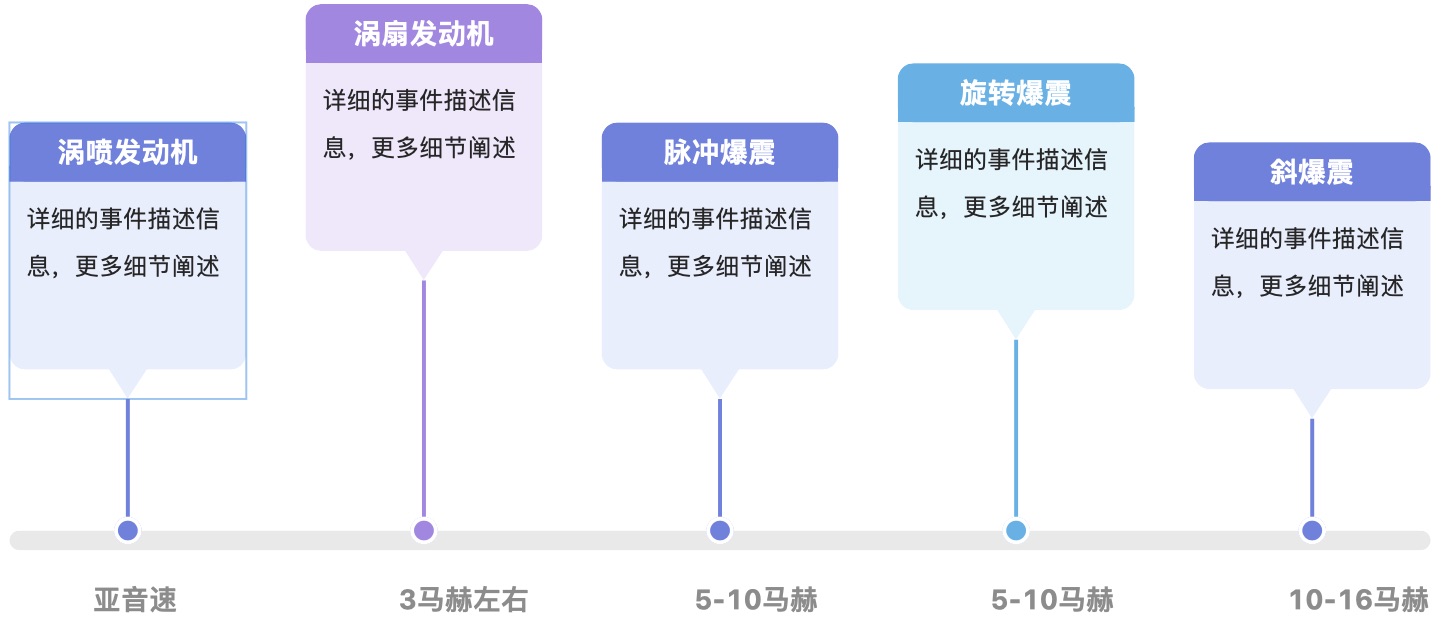
采用连续爆震发动机,或者在保持现有的结构下采用连续爆震的方式,如图3所示,可以大幅提升发动机的性能。因为连续爆震发动机有着自压缩的特点,发动机可以在较低的增压比下产生更大的有效功,减小了压气机的负载,相应地减少了压气机的级数,进而降低对涡轮做功能力的要求[2];同时,连续爆震还有更高的热效率。除了性能以外,连续爆震发动机还有着更低的NOx排放[6],对环境更友好。此外,传统的燃烧室需要减小空气来流速度,并对火焰进行稳定,防止高速气流将燃烧室内的火焰吹灭,这使得燃烧室的结构相比于连续爆震燃烧室而言复杂了不少。一般来说,在机械设计中,越简单的结构可靠性越高,在采用了连续爆震燃烧室后,燃烧室乃至整个核心机的结构可以简化,提高了发动机的可靠性。
高速飞行的飞机需要采用较小涵道比的发动机以降低阻力,因此,对于需要维持长时间超声速飞行的客机而言,采用涡喷发动机比涡扇发动机更合理,“协和”号和图-144超声速客机都采用了大推力的涡喷发动机。然而,涡喷发动机的热效率,尤其是在低速飞行时的热效率很低。以“协和”号飞机为例,由于超声速飞行时的噪声问题,被禁止在陆地上空以超声速飞行,仅在大西洋上空才能进行超声速飞行,而其在陆地上空亚声速飞行时耗油率很高,大约是同时代的波音747的两倍[7]。如何满足超声速和亚声速状态对于动力的不同需求,是决定目前新一代超声速客机研制成功与否的关键之一。
以GE公司为Aerion公司的AS2超声速客机研发的Affinity涡扇发动机为例,这型发动机采用了类似于CFM56的核心机,低压转子则经过了重新设计,由两级风扇和两级涡轮组成,以便更好地适应超声速飞行。Affinity发动机的设计巡航速度为Ma1.4,甚至比“协和”号的Ma1.7还低[7],这是对不同需求妥协的产物——采用Ma1.4的巡航速度可以在速度与航程之间取得平衡,并且AS2飞机也不是完全为超声速巡航而设计的,兼顾了亚声速飞行的需求,因此,Affinity发动机采用了对超声速飞行而言非常大的涵道比(3:1)。
化解这一矛盾的另一种解决方案是采用变循环发动机,如采用可以在涡扇模式和冲压模式中切换的发动机,可以较好地平衡超声速与亚声速飞行对于动力需求的矛盾。但是,传统结构的发动机要实现涡扇/冲压或涡扇/涡喷模式变循环是很复杂的。例如,SR-71侦察机便装备了J58涡喷/冲压变循环发动机,这台发动机可以在涡喷模式与冲压模式之间切换,但需要结构精密的进气道的配合;而GE公司为YF-23战斗机研发的YF120发动机,采用了复杂的机械结构在涡喷/涡扇模式之间转换。这些变循环发动机并不能满足民航飞机对经济性和可靠性的需求,而连续爆震发动机则为这一思路提供了更好的解决方案。
附注:
这篇文章大部分信息都是来源于互联网+论文直接摘取,我只是按我自己的框架把知识放在了一次,力求能够更完整的去把爆轰炸更全面和更系统的呈现在一篇文章中(然而实际是很难做到的)。因为个人觉得里面很多知识整理的还不够完整,有些拼凑感,所以还是希望再一次整理,所以暂时没有把参考文档放上来(估计会增加很多参考、
![[论文必备]最强科研绘图分析工具Origin(2)——简单使用教程](https://img-blog.csdnimg.cn/dea0e6079dcc4dbaa8f0edb87d9fcd10.gif)