目录
1、位置编码器的作用
2、代码演示
(1)、使用unsqueeze扩展维度
(2)、使用squeeze降维
(3)、显示张量维度
(4)、随机失活张量中的数值
3、定义位置编码器类,我们同样把它看作是一个层,因此会继承nn.Module
4、绘制词汇向量中特征的分布曲线
(1)、输出效果
(2)、输出效果分析
1、位置编码器的作用
- 因为在Transformers的编码器结构中,并没有针对词汇位置信息的处理,因此需要在Embedding层后加入位置编码器,将词汇位置不同可能会产生不同语义的信息加入到词嵌入张量中,以弥补位置信息的缺失
2、代码演示
(1)、使用unsqueeze扩展维度
position = torch.arange(0,10)
print(position.shape)
position = torch.arange(0,10).unsqueeze(1) #unsqueeze(0) 扩展第一个维度torch.Size([1, 10]),#unsqueeze(1) 扩展第二个维度torch.Size([10, 1])#unsqueeze(2) 是错误的写法
print(position)
print(position.shape)(2)、使用squeeze降维
x = torch.LongTensor([[[1],[4]],[[7],[10]]])
print(x)
print(x.shape)
y = torch.squeeze(x)
print(y.shape)
print(y)tensor([[[ 1],
[ 4]],
[[ 7],
[10]]])
torch.Size([2, 2, 1])
torch.Size([2, 2])
tensor([[ 1, 4],
[ 7, 10]])
在使用squeeze函数进行降维时,只有当被降维的维度的大小为1时才会将其降维。如果被降维的维度大小不为1,则不会对张量的值产生影响。因为上面的数据中第三个维度为1,所以将第三维进行降维,得到一个二维张量
(3)、显示张量维度
x = torch.LongTensor([[[1,2,3],[4,5,6]],[[7,8,9],[10,11,12]]])
print(x.size(0))
print(x.size(1))
print(x.size(2))
(4)、随机失活张量中的数值
m = nn.Dropout(p=0.2)
input = torch.rand(4,5)
output = m(input)
print(output)在张量中的 20 个数据中有 20% 的随机失活为0,也即有 4 个
3、定义位置编码器类,我们同样把它看作是一个层,因此会继承nn.Module
import torch
from torch.autograd import Variable
import math
import torch.nn as nn
class PositionalEncoding(nn.Module):def __init__(self,d_model,dropout,max_len=5000):""":param d_model: 词嵌入的维度:param dropout: 随机失活,置0比率:param max_len: 每个句子的最大长度,也就是每个句子中单词的最大个数"""super(PositionalEncoding,self).__init__()self.dropout = nn.Dropout(p=dropout)pe = torch.zeros(max_len,d_model) # 初始化一个位置编码器矩阵,它是一个0矩阵,矩阵的大小是max_len * d_modelposition = torch.arange(0,max_len).unsqueeze(1) # 初始一个绝对位置矩阵 max_len * 1div_term = torch.exp(torch.arange(0,d_model,2)*-(math.log(1000.0)/d_model)) # 定义一个变换矩阵,跳跃式的初始化# 将前面定义的变换矩阵进行奇数、偶数的分别赋值pe[:,0::2] = torch.sin(position*div_term)pe[:,1::2] = torch.cos(position*div_term)pe = pe.unsqueeze(0) # 将二维矩阵扩展为三维和embedding的输出(一个三维向量)相加self.register_buffer('pe',pe) # 把pe位置编码矩阵注册成模型的buffer,对模型是有帮助的,但是却不是模型结构中的超参数或者参数,不需要随着优化步骤进行更新的增益对象。注册之后我们就可以在模型保存后重加载时,将这个位置编码与模型参数一同加载进来def forward(self, x):""":param x: 表示文本序列的词嵌入表示:return: 最后使用self.dropout(x)对对象进行“丢弃”操作,并返回结果"""x = x + Variable(self.pe[:, :x.size(1)],requires_grad = False) # 不需要梯度求导,而且使用切片操作,因为我们默认的max_len为5000,但是很难一个句子有5000个词汇,所以要根据传递过来的实际单词的个数对创建的位置编码矩阵进行切片操作return self.dropout(x)
# 构建Embedding类来实现文本嵌入层
class Embeddings(nn.Module):def __init__(self,vocab,d_model):""":param vocab: 词表的大小:param d_model: 词嵌入的维度"""super(Embeddings,self).__init__()self.lut = nn.Embedding(vocab,d_model)self.d_model = d_modeldef forward(self,x):""":param x: 因为Embedding层是首层,所以代表输入给模型的文本通过词汇映射后的张量:return:"""return self.lut(x) * math.sqrt(self.d_model)
# 实例化参数
d_model = 512
dropout = 0.1
max_len = 60 # 句子最大长度
# 输入 x 是 Embedding层输出的张量,形状为 2 * 4 * 512
x = Variable(torch.LongTensor([[100,2,42,508],[491,998,1,221]]))
emb = Embeddings(1000,512)
embr = emb(x)
print('embr.shape:',embr.shape) # 2 * 4 * 512
pe = PositionalEncoding(d_model, dropout,max_len)
pe_result = pe(embr)
print(pe_result)
print(pe_result.shape)embr.shape: torch.Size([2, 4, 512])
tensor([[[-30.0099, 16.8963, 22.7739, ..., 39.4536, 34.2280, 17.5163],
[-30.3766, 26.1108, -8.2934, ..., -0.0000, -29.0978, 19.1214],
[-11.8387, 11.1781, -17.3273, ..., -39.4086, -18.5094, -20.4462],
[-38.0877, 31.2814, 16.9357, ..., 21.0642, 0.0000, -23.9738]],
[[-50.2344, 27.4659, -31.4892, ..., 7.2377, 32.1920, -15.7281],
[ 48.6540, 26.7432, -9.3068, ..., -37.7933, 27.0784, 21.6321],
[-11.6752, 8.3843, 0.3303, ..., 0.0000, -50.4058, -19.7049],
[ 27.9156, 0.8762, -11.5511, ..., -75.0058, 3.2941, 38.2998]]],
grad_fn=<MulBackward0>)
torch.Size([2, 4, 512])
4、绘制词汇向量中特征的分布曲线
import matplotlib.pyplot as plt
import numpy as np
# 创建一张 15 * 5 的画布
plt.figure(figsize=(15,5))
# 实例化一个PositionalEncoding类,得到pe编码矩阵
pe = PositionalEncoding(20, 0)
y = pe(torch.zeros(1,100,20))
# 定义画布的横坐标标,横坐标得到100的长度,纵坐标是某一个词汇中的某一个词汇中的某一维特征在不同长度下对应的值
plt.plot(np.arange(100),y[0,:,4:8].data.numpy())
# 在画布上显示维度提示信息
plt.legend(["dim %d" %p for p in [4,5,6,7]])(1)、输出效果
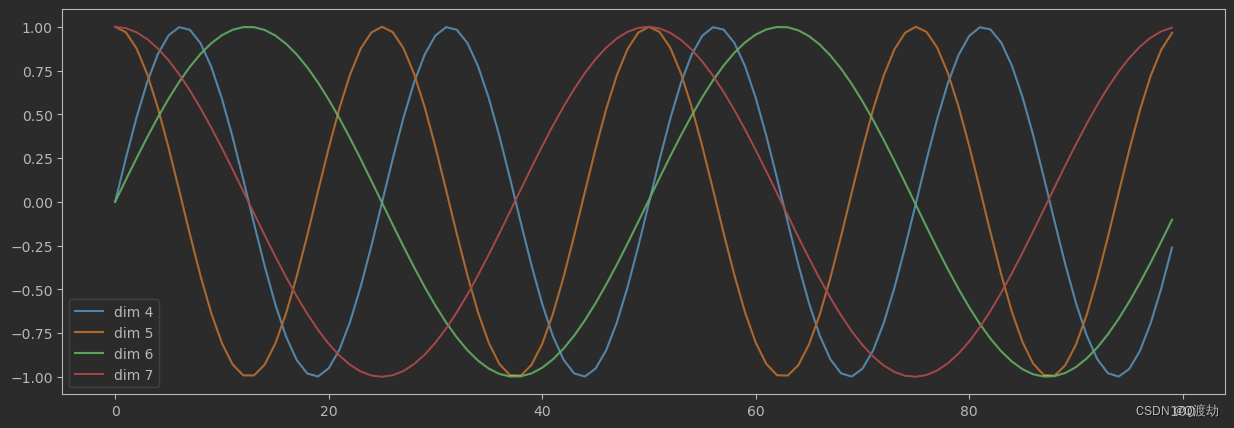
(2)、输出效果分析
- 每条颜色的曲线代表某一个词汇中的特征在不同位置的含义
- 保证同一词汇随着所在位置不同它对应位置嵌入向量会发生变化
- 正弦波和余弦波的值域范围都是从 1 到 -1 这又很好地控制了嵌入数值的大小,有助于梯度的快速计算