文章目录
- 前言
- B树基本规则
- B树的数据插入(文字描述+图解)
- B树数据查找
- B树效率分析
- B树的作用
- B+树基本规则
- B+树 与 B树对比
- B*树基本规则
- B*树 与 B+树对比
- 拓展
前言
B树基本规则
-
每个节点最多有m个子节点,其中m是一个正整数。根节点除外,其他节点至少有⌈m/2⌉个子节点。
-
每个节点中的键值按照非降序排列。对于节点中的键值k,如果有n个子节点,那么节点中的n-1个键值将把节点分为n个区间,第i个区间的键值小于k,第i+1个区间的键值大于等于k。
-
所有叶子节点位于同一层,且不包含任何键值信息,可以看作是外部存储的块。
-
每个非叶子节点中的键值个数比子节点个数少1。
-
每个节点中的键值个数满足:
⌈m/2⌉-1 <= 键值个数 <= m-1

B树的数据插入(文字描述+图解)
插入规则概览:
1.从根节点开始,按照节点中的键值进行比较,找到合适的叶子节点(比较结果类似于二叉搜索树)。
2.如果叶子节点中已经存在该键值,则更新相应的值。
3.如果叶子节点中不存在该键值,则将键值插入到叶子节点的合适位置,并保持节点中的键值有序。
4.如果插入键值后,叶子节点的键值个数超过了上限m-1,则进行分裂操作。
将叶子节点的键值分成两部分,左边部分包含⌈(m-1)/2⌉个键值,右边部分包含⌊(m-1)/2⌋个键值。将右边部分的键值和对应的子节点分离出来,形成一个新的叶子节点。将新的叶子节点插入到叶子节点的右边,并更新父节点的键值信息。
5.如果插入键值后,叶子节点的键值个数没有超过上限m-1,则直接插入。
6.如果父节点存在并且插入键值后超过了上限m-1,则进行分裂操作。
将父节点的键值分成两部分,左边部分包含⌈(m-1)/2⌉个键值,右边部分包含⌊(m-1)/2⌋个键值。将右边部分的键值和对应的子节点分离出来,形成一个新的父节点。将新的父节点插入到父节点的右边,并更新祖父节点的键值信息。
重复步骤6,直到根节点为止。
(图解)插入的情况归类为以下几种:
-
无父亲节点,不需要分裂;
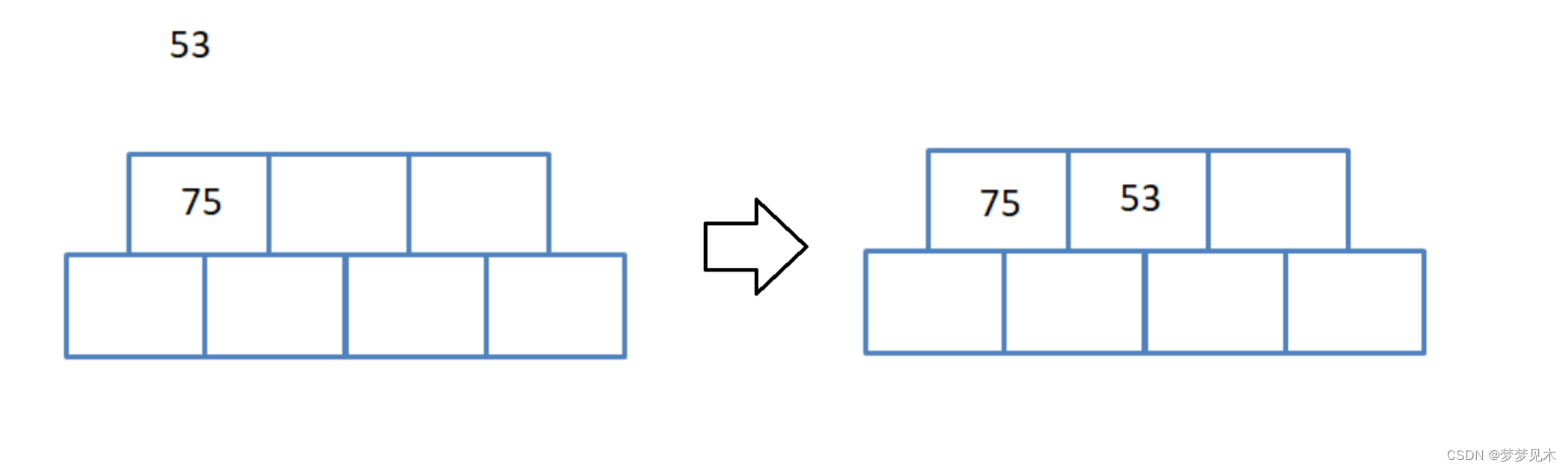
-
有父亲节点,不需要分裂;
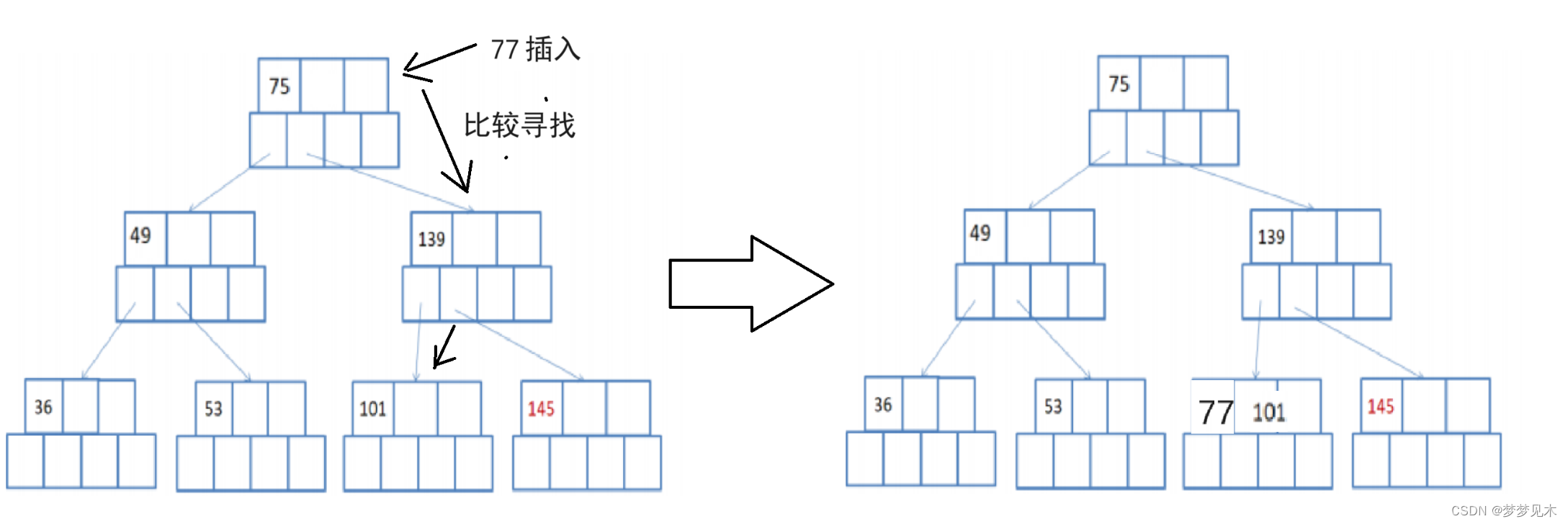
-
无父亲节点,需要分裂;
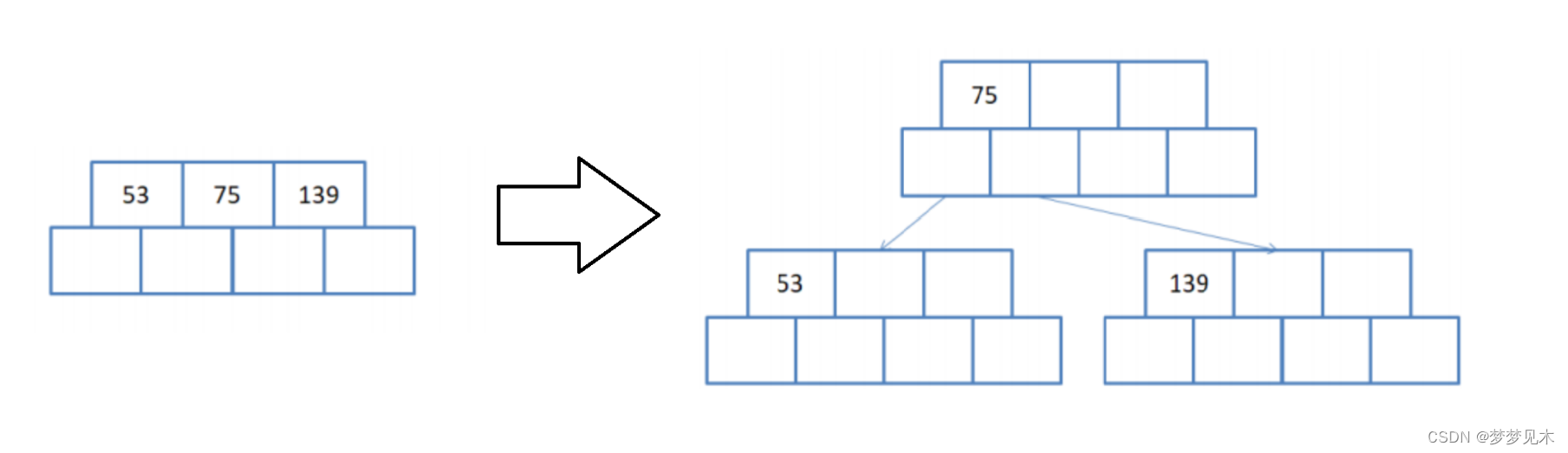
将叶子节点的键值分成两部分,左边部分包含⌈(m-1)/2⌉个键值,右边部分包含⌊(m- 1)/2⌋个键值。将右边部分的键值和对应的子节点分离出来,形成一个新的叶子节点。 -
有父亲节点,插入节点需要分裂,插入后父亲节点不需要分裂;
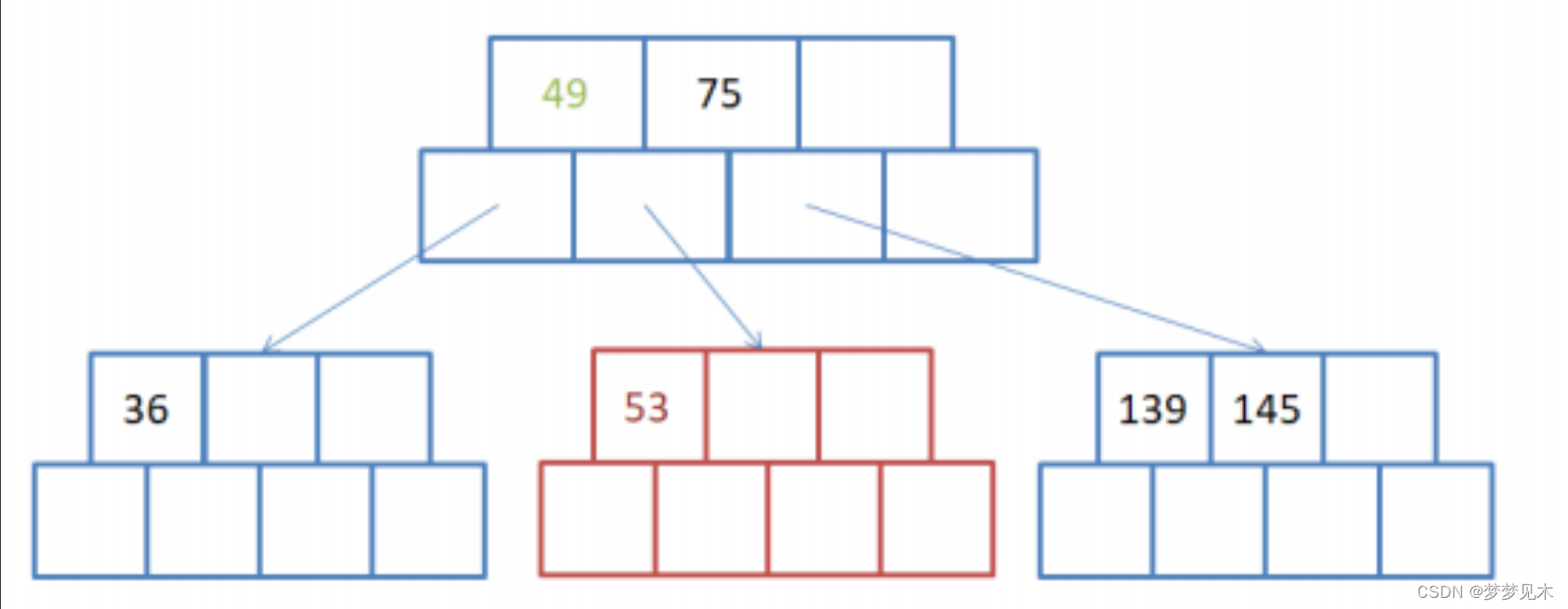
将叶子节点的键值分成两部分,左边部分包含⌈(m-1)/2⌉个键值,右边部分包含⌊(m-1)/2⌋个键值。
将右边部分的键值和对应的子节点分离出来,形成一个新的叶子节点。将新的叶子节点插入到叶子节点的右边,并更新父节点的键值信息。
-
有父亲节点,插入节点需要分裂,插入后父亲节点需要分裂;
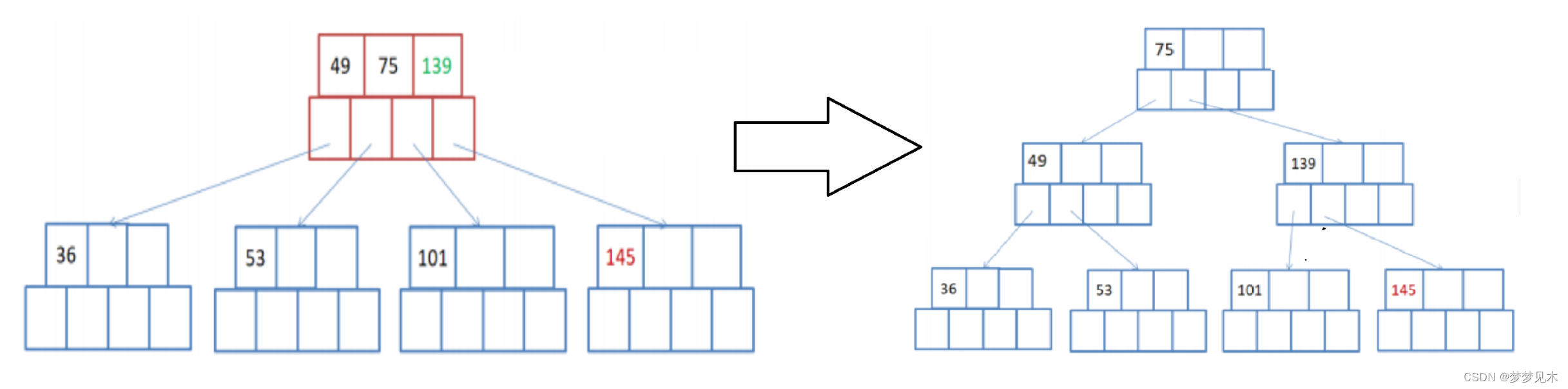
将父节点的键值分成两部分,左边部分包含⌈(m-1)/2⌉个键值,右边部分包含⌊(m-1)/2⌋个键值。将右边部分的键值和对应的子节点分离出来,形成一个新的父节点。将新的父节点插入到父节点的右边,并更新祖父节点的键值信息。重复以上步骤,直到根节点
B树数据查找
由于数据数据排列的格式类似于搜索二叉树,所以查找也是。
B树效率分析
如果忽略内存中查找和外存中查找时间的巨大差异:
设 :
有效值个数 = N;
度 = M ;
则:一个节点的有效值个数 = M/2 ~ M-1 ;
故:树的高度为 = log{M/2} N ~ log{M-1}N ;
一个节点内查找的复杂度 = O(log{2}M/2 ) ~ O(log{2}M-1 ) ;
故:最终时间复杂度 = [ O(log{2}M/2 ) ~ O(log{2}M-1 ) ] * [ log{M/2} N ~ log{M-1}N ]
但,实际应用情况不是这样,实际时间主要消耗在,从上级节点访问下级节点的过程中,因为访问节点其实是访问外存;
(关键理解点)B树查找过程中,IO操作即为进入节点的操作,当查找过程中需要访问到磁盘上的节点时,就需要进行IO操作将节点从磁盘读取到内存中。
所以主要的时间消耗为:[ log{M/2} N ~ log{M-1}N ] 次访问外存的次数 !!!!
对于N = 62*1000000000个节点,如果度M为1024,则 l o g M / 2 N log_{M/2}N logM/2N <=
4,即在620亿个元素中,如果这棵树的度为1024,则需要小于4次即可定位到该节点,然后利用二分查找可以快速定位到该元素,大大减少了读取磁盘的次数。
B树的作用
数据库索引:B树常被用作数据库的索引结构,能够高效地支持数据的查找和范围查询。
文件系统:B树被用于文件系统中的目录结构,可以高效地支持文件的查找和管理。
缓存系统:B树可以用于缓存系统中的索引结构,加速数据的访问和查询。
路由表:B树可以用于路由表的存储和查找,快速定位目标地址。
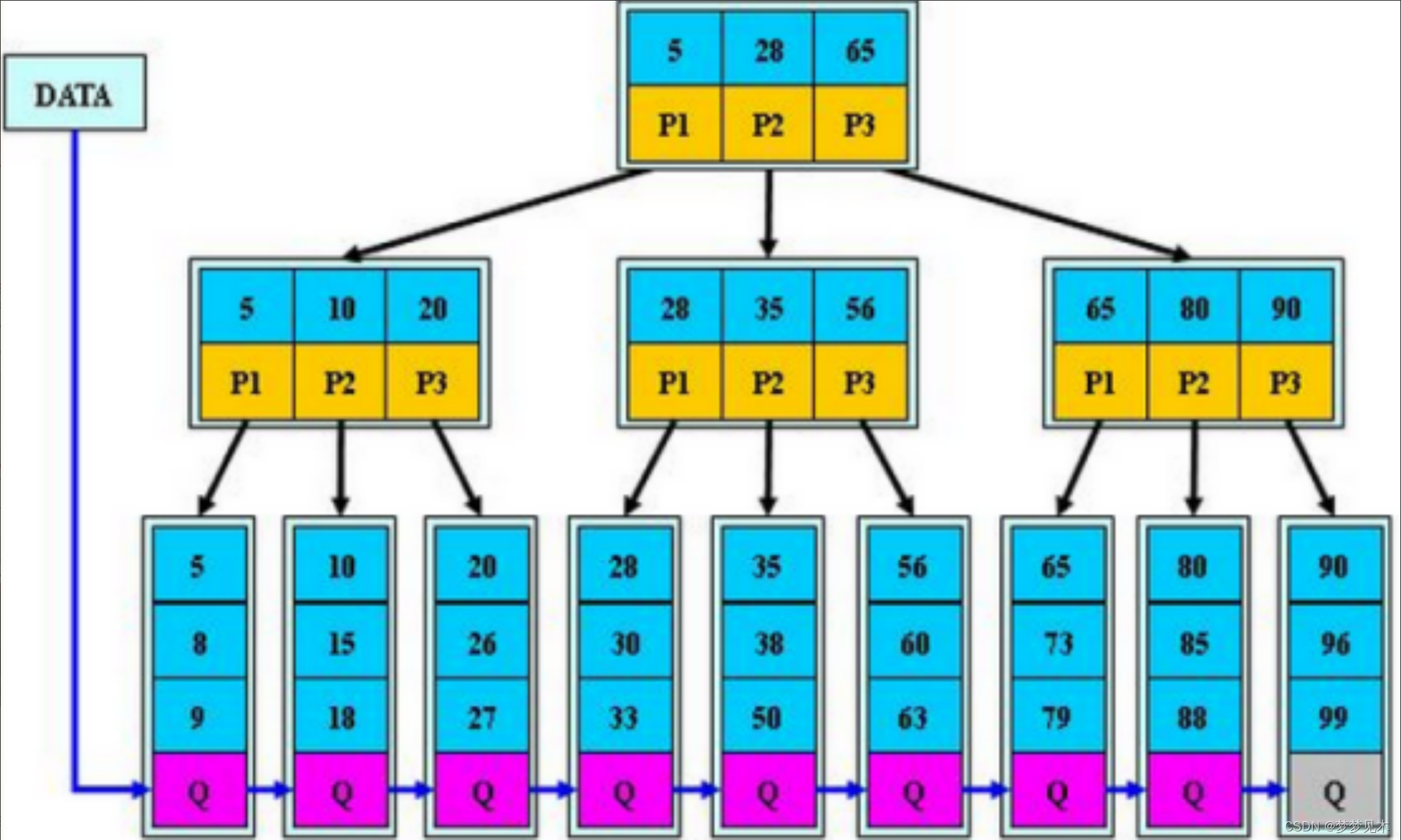
B+树基本规则
- 分支节点的子树指针与关键字个数相同
- 分支节点的子树指针p[i]指向关键字值大小在[k[i],k[i+1])区间之间
- 所有叶子节点增加一个链接指针链接在一起
所有关键字及其映射数据都在叶子节点出现(所有的数据都在最底一层存储) - 所有关键字都出现在叶子节点的链表中,且链表中的节点都是有序的。
- 不可能在分支节点中命中数据(所有的数据都在最底一层存储)
- 分支节点相当于是叶子节点的索引,叶子节点才是存储数据的数据层。
B+树 与 B树对比
先说结论:
1.B树更适合随机查找,B+树更适合范围查找
2.B+树相对更省空间
3.对数据进行插入、删除的时候B+树更高
原因:
- B树的每个节点包含关键字和对应的指针,用于存储数据和构建索引。B树的节点可以直接存储数据,因此在查找时可以直接定位到数据所在的节点。
B+树的每个节点只包含关键字,数据存储在叶子节点中。叶子节点之间通过指针连接形成一个有序链表,叶子节点上的关键字也构成一个有序序列。B+树的非叶子节点仅用于索引,不存储数据,这样可以减少非叶子节点的数量,提高内存利用率。 - B树的节点既存储数据又存储索引,因此每个节点可以存储更多的数据。这样可以减少树的高度,提高查询效率。但是,由于B树的节点包含数据,插入和删除操作需要进行数据的移动和调整,相对较慢。
B+树的非叶子节点仅用于索引,不存储数据,因此每个节点可以存储更多的索引。叶子节点之间通过指针连接形成有序链表,可以高效地进行顺序访问。同时,由于B+树的数据只存储在叶子节点中,插入和删除操作只需要调整索引节点,相对较快。
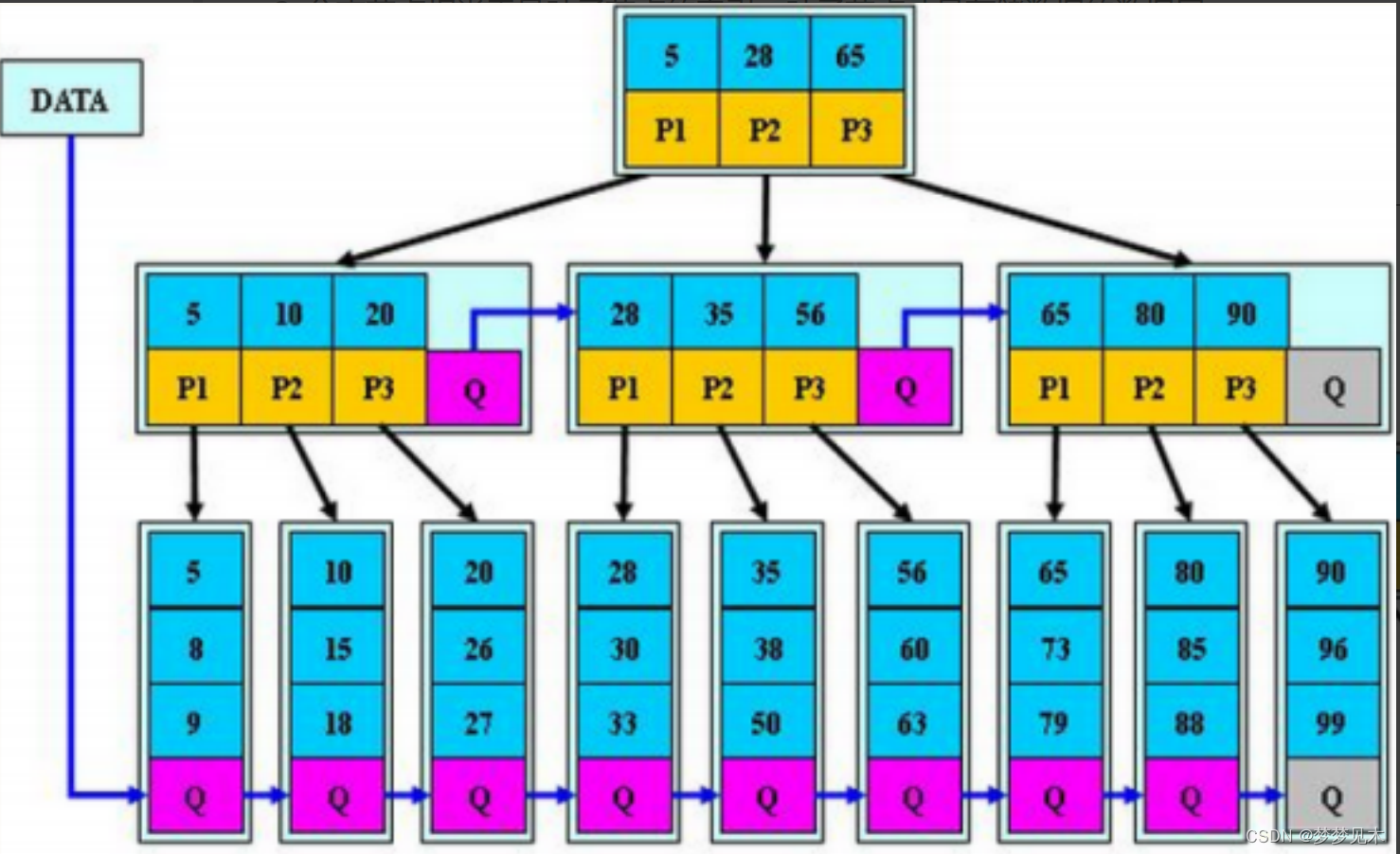
B*树基本规则
B*树是B+树的变形,在B+树的非根和非叶子节点再增加指向兄弟节点的指针。
B*树 与 B+树对比
结论: B*树空间利用率比B+树高
B+树的分裂:当一个结点满时,分配一个新的结点,并将原结点中1/2的数据复制到新结点,最后在父结点中增加新结点的指针;
B*树的分裂:当一个结点满时,如果它的下一个兄弟结点未满,那么将一部分数据移到兄弟结点中,再在原结
点插入关键字,最后修改父结点中兄弟结点的关键字(因为兄弟结点的关键字范围改变了);如果兄弟也满了,则在原结点与兄弟结点之间增加新结点,并各复制1/3的数据到新结点,最后在父结点增加新结点的指针。
拓展
B+树的插入操作规则如下:
查找插入位置:从根节点开始,按照B+树的搜索规则找到插入位置。如果插入的关键字已经存在于树中,则根据具体情况进行处理(如替换、忽略或合并等)。
插入到叶子节点:将新的关键字插入到叶子节点中的适当位置。如果插入后导致叶子节点的关键字数量超过了阶数的上限,则进行分裂操作。
叶子节点分裂:将超过阶数上限的叶子节点分裂成两个节点。将一半的关键字移动到新的节点中,并调整指针连接。同时,将新节点的最小关键字插入到父节点中。
父节点调整:如果叶子节点的分裂导致父节点关键字数量超过了阶数的上限,则进行递归的分裂操作。将超过阶数上限的父节点分裂成两个节点,并将新节点的最小关键字插入到父节点的父节点中。
递归调整:如果父节点的分裂导致祖先节点关键字数量超过了阶数的上限,则继续进行递归的分裂操作,直到根节点。
根节点分裂:如果根节点的分裂导致树的高度增加,则创建一个新的根节点,并将原来的根节点分裂成两个节点。将新的根节点的最小关键字插入到新的根节点中,并调整指针连接。