本文来讲一下PID调节器。
在实际的系统中,因为摩擦、阻力等外界因素的存在,系统的实际输出与我们期望的输出通常存在误差,PID的目的就是调节系统的实际输出,使其更快更稳地贴近期望输出。
PID模块被周期性的调用,模块的输入是实际输出与期望输出之间的误差值,模块的输出是一个补偿,这个补偿输入给系统,使得系统的输出增大或减小,逐步贴近期望输出。
这里需要注意一下,系统的输出不可能阶跃性的增加,是需要时间的,比如车辆提速、水位升高等。PID模块通过控制系统的输入,使得系统的输出在一个PID周期内增加所期望的补偿值。其实可以理解为PID输入给系统的是一个加速度,或输出曲线增长的斜率。
P —— 比例调节
PID中的P是比例调节,就是每次将误差值乘以一个比例系数(后文称为P),输入给系统。比如,期望输出是10,当前系统输出是2,那么误差是8,假设P是0.5,那么补偿就是8*0.5=4,输入给系统,系统输出变成6。下一个调节周期中,误差变为4,补偿变为2,系统输出变为8。以此类推,我们可以知道系统输出最终会无限接近于期望输出。且比例系数越大,调节速度越快。
上述系统是一个理想系统,即我们输入的补偿是多少,输出就增加多少。该系统中输入函数x(t)是一个单位阶跃函数,输出函数y(t)是对输入参数x在0-t时段内的定积分,反之则是输入参数x是y(t)的导数,即斜率,这个从后面的曲线中也可以看出来。y(t)是一个斜坡函数,所以系统的传递函数H(s) = Y(s) / X(s) = (1/s²) / (1/s) = 1/s,用simulink建模如下:

设置PID运行周期为1S,PID模块中参数P设置为0.5,运行结果如下,红色是期望输出,黄色是PID计算得到的补偿,蓝色是系统实际输出。我们可以看到PID的输出是系统输出曲线的斜率。
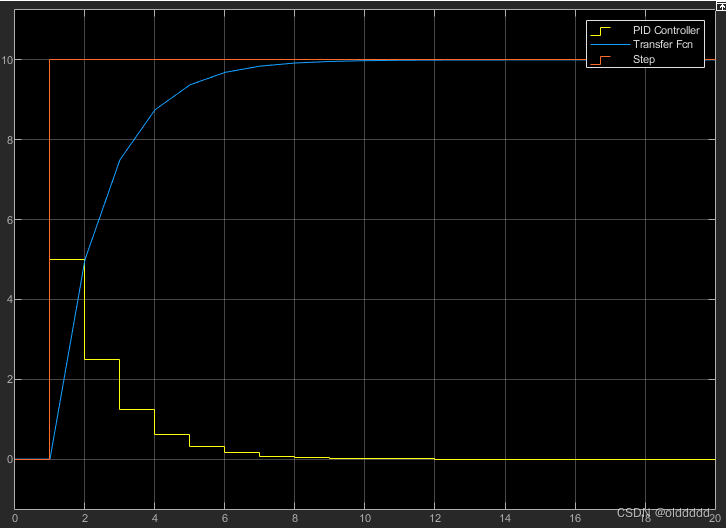
P越大,系统输出收敛的越快,下图P=0.8:
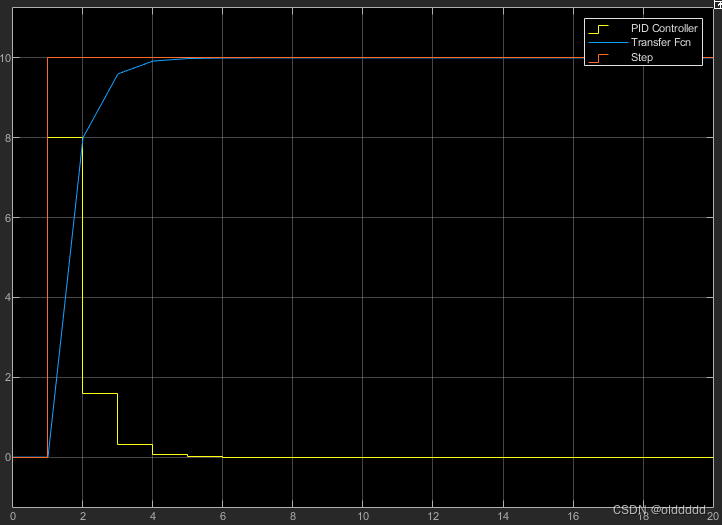
把P设置为1,运行结果如下,也就是说一个PID周期直接把系统输出调节到了期望输出:
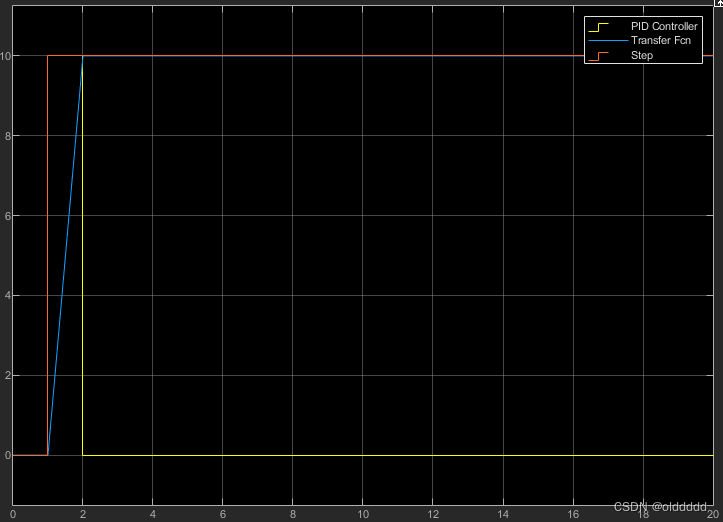
当P大于1的时候,系统输出就会出现震荡,下图为P=1.5:
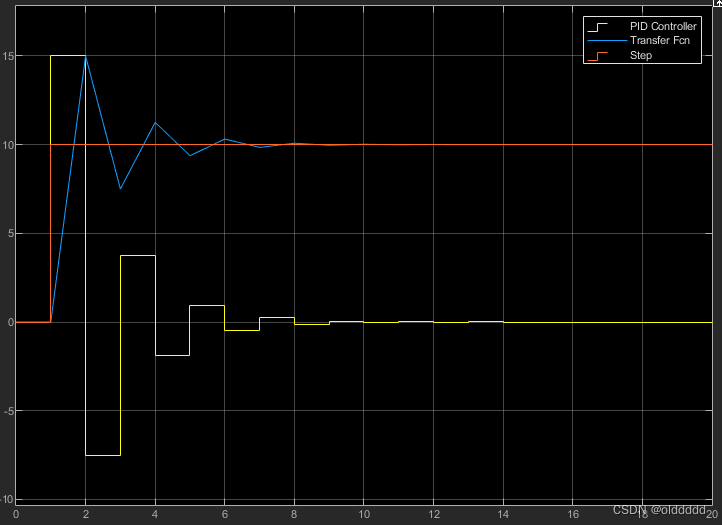
当P大于等于2时,系统就无法进入稳定状态,下图为P=2.1:
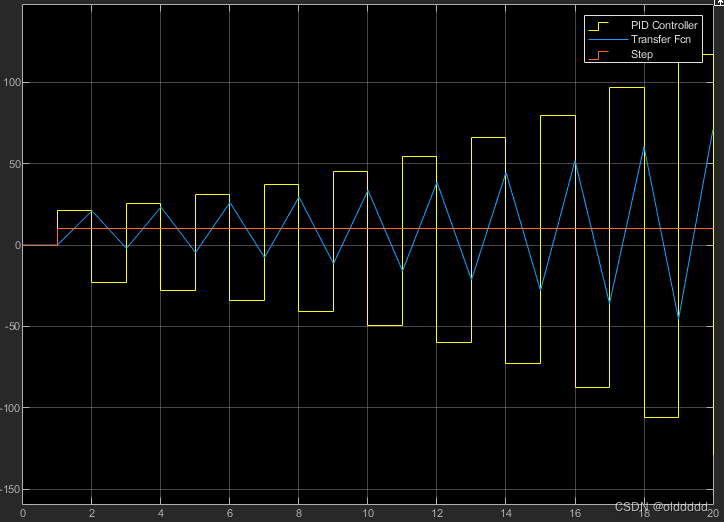
但是实际系统中会存在阻力和误差,比如在一个PID调节周期内,摩擦等因素会使系统的输出降低1,还是用上面的例子,P设置为0.5,当系统的输出 ≥ 8的时候,PID输出的补偿就会 ≤ 1,即输入给系统的补偿量小于系统在一个周期内的损耗,这时系统的输出将永远也无法达到预期的输出10,只会稳定在8附近。这个就叫稳态误差,只有P的调节器无法消除稳态误差,P的作用是能使输出快速向期望输出靠拢。
我们在simulink中创建上述存在摩擦的系统,摩擦使系统的输出降低1,可以看作是系统始终有一个-1的输入(理想系统为y = x,损耗为y = -1,两者相加即 y = x - 1),所以修改模型如下,在系统的输入上叠加一个值为-1的常量:
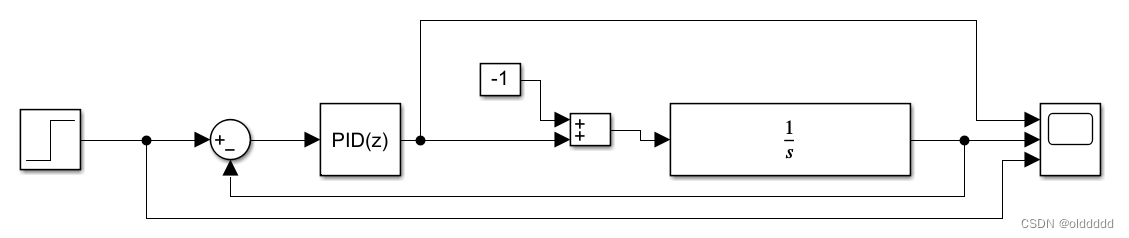
仿真结果如下,我们可以看到系统输出最终稳定在8附近:
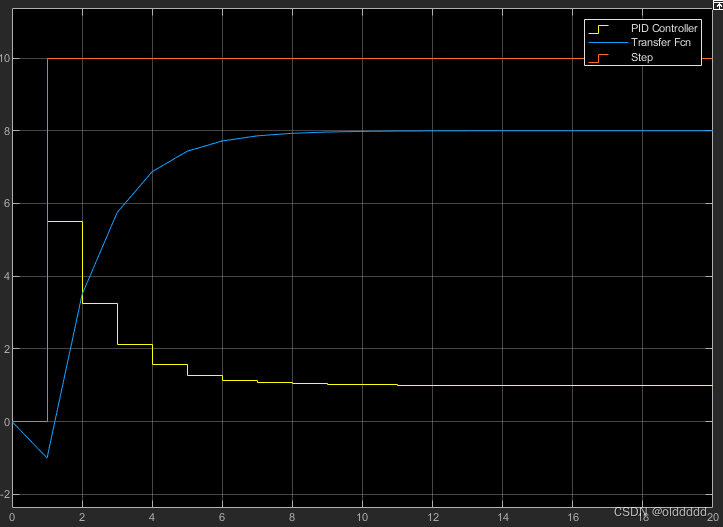
把叠加的输入改为-2,系统稳定在6附近;
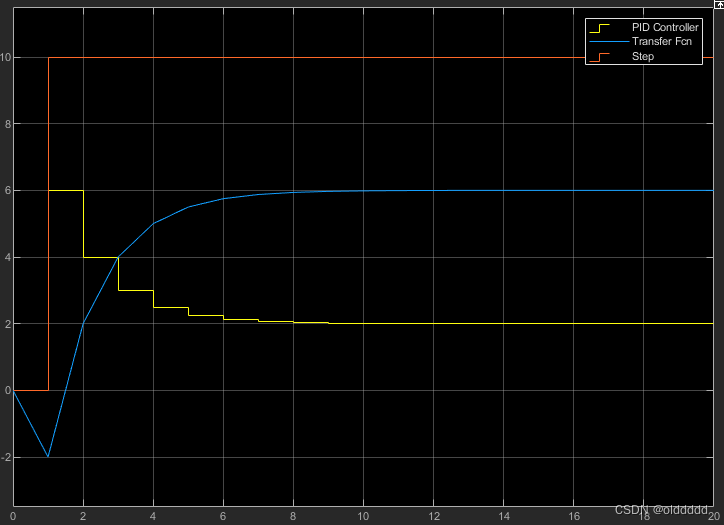
I —— 积分调节
要想消除稳态误差,就要用到PID中的I了,I是指积分,是把前面所有的误差值加起来,再乘以一个系数,作为一个补偿输入给系统。也就是说只要误差不为0,那么PID计算得到的补偿值就会持续增大,直到误差为0,所以I调节器能消除稳态误差。
我们将PID控制器的参数设置如下:
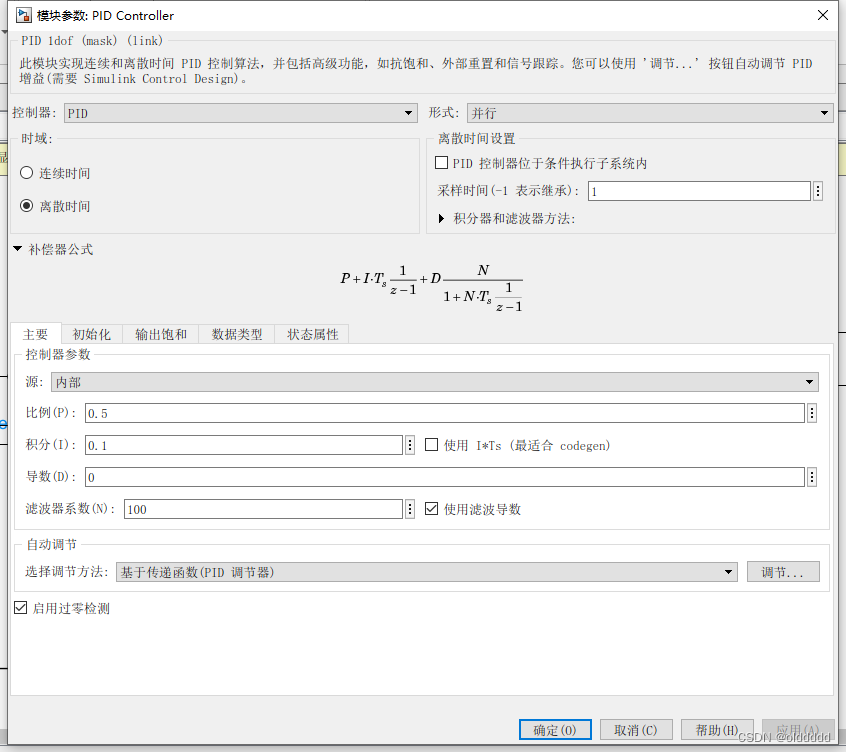
仿真结果如下:
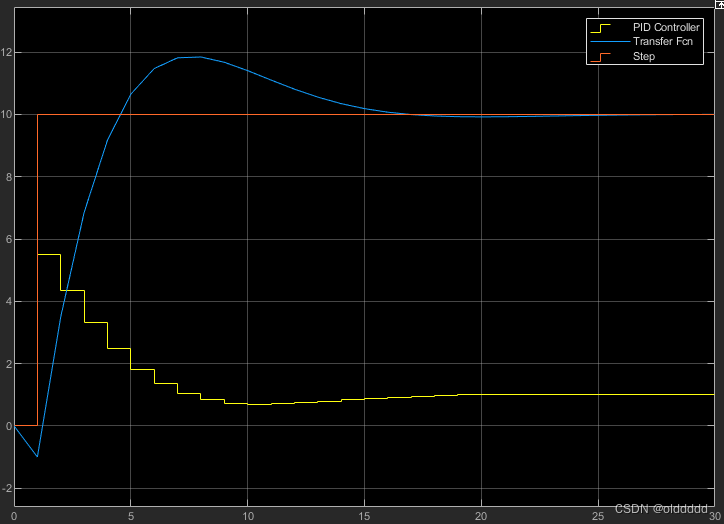
可以看到稳态误差被消除了,但出现了振荡,I系数越大,稳态误差消除得越快,但振荡可能会更大,下图是把I设置为0.2的仿真结果:
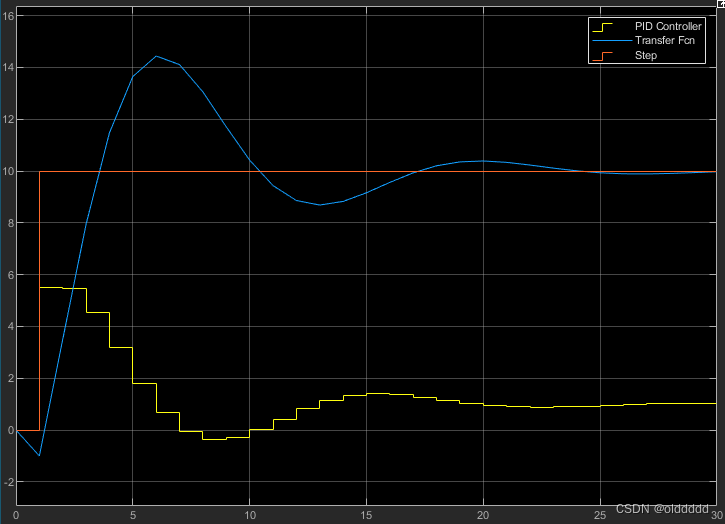
D —— 微分调节
如何解决引入I之后导致的振荡问题呢,就要用到PID中的D了,D是指微分,误差的微分就是误差变化的快慢,当系统输出逐渐接近期望输出的时候,误差的变化率总是越来越小的,把这个变化率乘以微分系数D,再叠加到补偿上,能使系统输出在前期快速增加,在接近期望输出的时候增加的更慢,从而达到抑制振荡的效果。我们下面看一个更复杂一点的系统模型:

PID模块参数先设置如下,不加微分补偿:
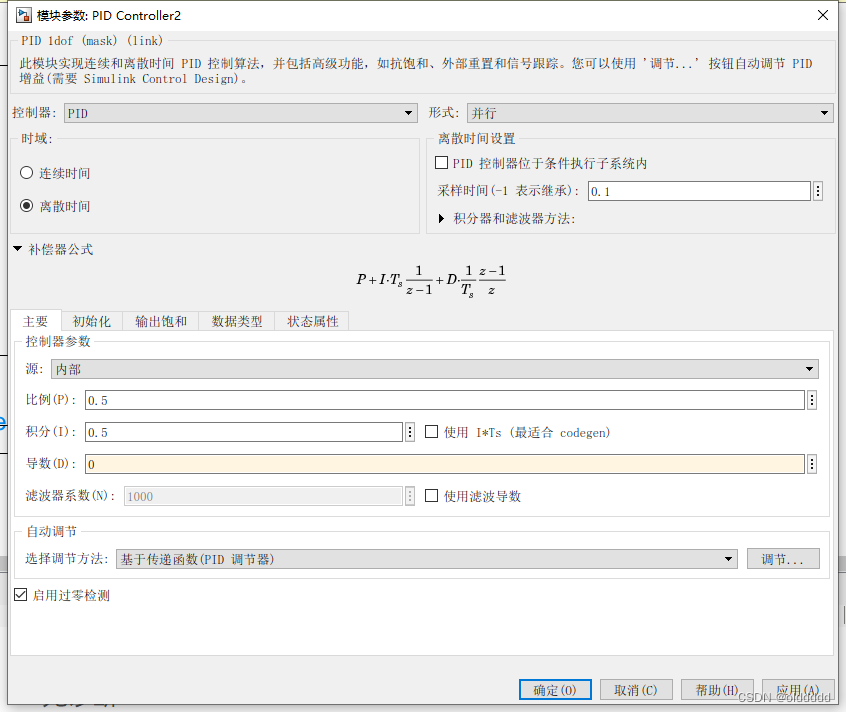
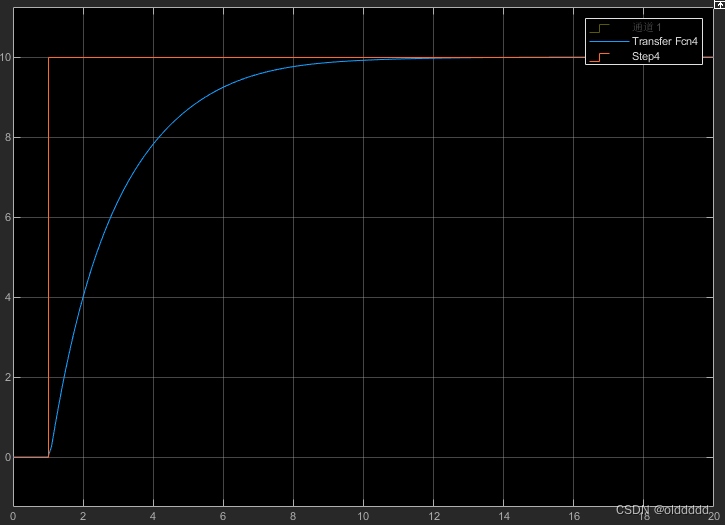
仿真结果如下:
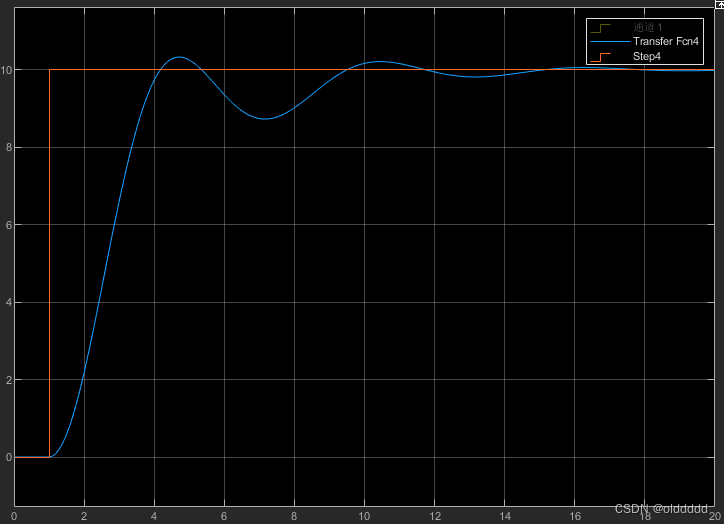
再把参数D设置为0.5,仿真结果如下,可以看到振荡被很好地抑制了:
但是微分调节在实际工作中并不常用,因为微分调节在实际应用中往往会引入噪声,导致系统不稳定。通常只用到PI两个调节器。