目录
1.ID3算法
2.C4.5算法
3.信息增益率
(1)信息增益率
(2)案例
4.决策树的剪枝
5.总结
(1)优点与改进
(2)缺点
(3) 总结及展望
近年来决策树方法在机器学习、知识发现等领域得到了广泛应用。数据挖掘作为一种发现大量数据中潜在信息的数据分析方法和技术已经成为各界关注的热点。其中,决策树以其出色的数据分析效率、直观易懂等特点倍受青睐。构造决策树有多种算法,国际上最早的、具有影响力的决策树是由Quinlan于1986年提出的ID3算法,是基于信息熵的决策树分类算法。ID3算法采用信息熵作为属性选择标准,可这个标准易偏向于取值较多的候选属性。Quinlan于1993年又提出了ID3的改进版本C4.5算法,C4.5算法用信息增益率来选择决策属性,它继承了ID3算法的全部优点,在ID3的基础上还增加了对连续属性的离散化、对未知属性的处理和产生规则等功能。
1.ID3算法
当前最有影响的决策树算法是Quinlan于1986年提出的ID3和1993年提出的C4.5算法。ID3算法是较早出现也是最著名的决策树归纳算法。C4.5是ID3的改进算法不仅可以处理离散值属性,还能处理连续值属性。
ID3算法存在着属性偏向、对噪声敏感等问题。
1983年,T. Niblett和 A.Patterson在 ID3算法的基础上提出了ACLS Algorithm。该算法可以使属性取任意三、C4.5算法的整数值,这扩大了决策树算法的应用范围。
1984年,I.Kononenko、E.Roskar和 I.Bratko 在 ID3算法的基础上提出了ASSISTANT Algorithm,它允许类别的取值之间有交集。
1984年,A. Hart提出了Chi——Square统计算法,该算法采用了一种基于属性与类别关联程度的统计量。
L.Breiman、C.Ttone、R. Olshen和 J. Freidman在1984年提出了决策树剪枝概念,极大地改善了决策树的性能。
1986年,T.Niblett提出了Minimum— Error PruningAlgorithm。1987年,J.R.Quinlan提出了Reduced Error Pruning Algorithm。1987年,J. Mingers提出了Critical Value Pruning Algorithm。1992年,K.Kira和L. Rendell提出了RELIEF Algorithm,该算法是决策树算法发展史上一座里程碑。
2.C4.5算法
C4.5算法与ID3相似,在ID3的基础上进行了改进,采用信息增益比来选择属性。ID3选择属性用的是子树的信息增益,ID3使用的是熵(entropy, 熵是一种不纯度度量准则),也就是熵的变化值,而C4.5用的是信息增益率。
3.信息增益率
在ID3算法中,显然属性的取值越多,信息增益越大。为了避免属性取值个数的影响,C4.5算法从候选划分中找出信息增益高于平均水平的属性,再从中选出信息增益率(用信息增益除以该属性本身的固有值(Intrinsic value)最高的分类作为分裂规则。信息增益比本质就是在信息增益的基础之上乘上一个惩罚参数。特征个数较多时,惩罚参数较小;特征个数较少时,惩罚参数较大。信息增益比就等于惩罚参数 * 信息增益。
(1)信息增益率
信息增益率:增益率是用前面的信息增益Gain(D, a)和属性a对应的"固有值"(intrinsic value)的比值来共同定义的。属性 a 的可能取值数目越多(即 V 越大),则 IV(a) 的值通常会越大。

(2)案例
根据‘天气’,‘温度’,‘湿度’,‘风速’四个属性判断活动是否进行(进行、取消)。

该数据集有四个属性,属性集合A={ 天气,温度,湿度,风速}, 类别标签有两个,类别集合L={进行,取消}。
a.计算类别信息熵
类别信息熵表示的是所有样本中各种类别出现的不确定性之和。根据熵的概念,熵越大,不确定性就越大,把事情搞清楚所需要的信息量就越多。

b.计算每个属性的信息熵
每个属性的信息熵相当于一种条件熵。他表示的是在某种属性的条件下,各种类别出现的不确定性之和。属性的信息熵越大,表示这个属性中拥有的样本类别越不“纯”。

c.计算信息增益
信息增益的 = 熵 - 条件熵,在这里就是 类别信息熵 - 属性信息熵,它表示的是信息不确定性减少的程度。如果一个属性的信息增益越大,就表示用这个属性进行样本划分可以更好的减少划分后样本的不确定性,当然,选择该属性就可以更快更好地完成我们的分类目标。

d.计算属性分裂信息度量
用分裂信息度量来考虑某种属性进行分裂时分支的数量信息和尺寸信息,我们把这些信息称为属性的内在信息(instrisic information)。信息增益率用信息增益/内在信息,会导致属性的重要性随着内在信息的增大而减小(也就是说,如果这个属性本身不确定性就很大,那我就越不倾向于选取它),这样算是对单纯用信息增益有所补偿。
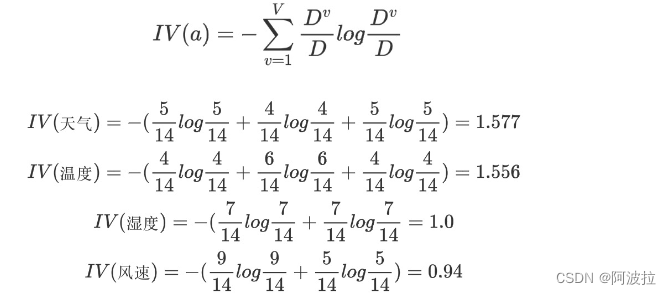
e.计算信息增益率
天气的信息增益率最高,选择天气为分裂属性。发现分裂了之后,天气是“阴”的条件下,类别是”纯“的,所以把它定义为叶子节点,选择不“纯”的结点继续分裂。

4.决策树的剪枝
剪枝即是删除一些最不可靠的分枝,用多个类的叶节点代替,以加快分类的速度和提高决策树正确分类新数据的能力。常用的剪枝方法有预剪枝和后剪枝: 预剪枝就是提早结束决策树的构造过程,通过选取一个阈值判断树的构造是否停止,因为适当的阈值很难界定,所以预剪枝存在危险,不能保证树的可靠性; 后剪枝是在决策树构造完毕后得到一棵完整的树再进行剪枝,通常的思想是对每个树节点进行错误估计,通过与其子树的错误估计的比较,来判断子树的裁剪,如果子树的错误估计较大,则被剪枝,最后用一个独立的测试集去评估剪枝后的准确率,以此得到估计错误率最小的决策树。
C4.5剪枝技术是基于悲观错误的后剪枝方法,首先把构造的决策树转换成规则集合,然后通过删去某些条件来使得规则变短或变少。
5.总结
(1)优点与改进
C4.5算法是用于生成决策树的一种经典算法,是ID3算法的一种延伸和优化。C4.5算法对ID3算法主要做了一下几点改进:
- 通过信息增益率选择分裂属性,克服了ID3算法中通过信息增益倾向于选择拥有多个属性值的属性作为分裂属性的不足;
- 能够处理离散型和连续型的属性类型,即将连续型的属性进行离散化处理;
- 构造决策树之后进行剪枝操作;
- 能够处理具有缺失属性值的训练数据。 C4.5算法训练的结果是一个分类模型,这个分类模型可以理解为一个决策树,分裂属性就是一个树节点,分类结果是树的结点。每个节点都有左子树和右子树,结点无左右子树。
- C4.5采用二分法处理连续特征,将连续特征进行排列,将连续两个值的中间值作为分裂节点,将小于该值和大于该值的样本分为两个类别,找到信息增益最大的分裂点,本质上还是用的离散特征。需注意的是,与离散属性不同,若当前节点划分属性为连续属性,该属性还可作为其后代节点的划分属性。
- 在属性值缺失的情况下划分属性,将数据集分成两部分:没有缺失值的部分、有缺失值的部分。对每个样本设置一个权重,将没有缺失值的部分按照占据总样本的比例计算信息增益率,并乘上所占比例。
- 给定划分属性,若样本在该属性上缺失时,若样本x在划分属性a上的取值未知,则将x同时划入所有子节点,且样本权值按所占比例和样本权值进行调整。直观地看,这就是让同一个样本以不同的概率划入到不同的子节点中。
(2)缺点
- 信息增益率采用熵的计算,里面有大量耗时的对数计算。
- 多叉树的计算效率不如二叉树高。
- 决策树模型容易过拟合,所以应该引入剪枝策略进行处理。
(3) 总结及展望
C4.5算法作为分类规则的经典算法,得到了业界的普遍肯定,不过决策树尽管分类较快和预测精度高,但是构造的树不够小,存在碎片和过度拟合的情况,针对 C4.5决策树算法的不足,如何改进和优化算法,还存在不少问题亟待解决,这正是今后的研究方向,主要有:
1.要找到最优的决策树是NP问题,必须寻找更好的方法,将决策树技术和其它新兴技术相结合,取长补短,提高决策树的抗噪声能力和准确性。
2.研究属性间的相关性对决策树产生的影响,以及如何利用或者消除这些相关性来构造决策树,值得关注。
3.决策树技术中如何处理时间复杂度和分类准确性之间的矛盾,一直以来都是一个令人感兴趣的问题。怎样在提高准确度的前提下降低时间复杂度,是今后研究的一个重点及难点。
4.决策树技术软件化一直是决策树技术的方向之一。如何开发出功能更加强大、使用更加方便、界面更加友好的软件以实现决策树技术,是今后需努力实现的目标。