2894. 分类求和并作差
一、题目
给你两个正整数 n 和 m 。
现定义两个整数 num1 和 num2 ,如下所示:
num1:范围[1, n]内所有 无法被m整除 的整数之和。num2:范围[1, n]内所有 能够被m整除 的整数之和。
返回整数num1 - num2。
示例
输入:n = 10, m = 3
输出:19
解释:在这个示例中:
- 范围 [1, 10] 内无法被 3 整除的整数为 [1,2,4,5,7,8,10] ,num1 = 这些整数之和 = 37 。
- 范围 [1, 10] 内能够被 3 整除的整数为 [3,6,9] ,num2 = 这些整数之和 = 18 。
返回 37 - 18 = 19 作为答案。
提示:
- 1 <= n, m <= 1000
二、题解
- 思路:(求出范围[1,n]的整数和) - (求出[1,n]內能够被整除的整数和)*2
/*** @param {number} n* @param {number} m* @return {number}*/
var differenceOfSums = function(n, m) {const sum1 = add(n);const sum2 = m * add(Math.floor(n/m)) return sum1 - sum2*2;
};var add = function(n){if(n==1 || n ==0){return n;}else{return add(n-1)+n;}
}
这里我写了一个函数,专门用来求1+2+…+n 的和
优化:使用等差数列求和的公式,免去新建一个函数,循环计算
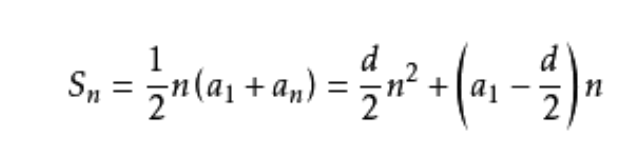
和=(首项+末项)×项数÷2
➡️ 1+2+3+…+n = n*(n+1) / 2
优化后
var differenceOfSums = function(n, m) {let sum1 = n * (n + 1)/2;// 能够被 m 整除的项数const num = Math.floor(n/m);const sum2 = m * num * (num + 1) / 2;return sum1 - sum2 * 2;
};