【算法训练-回溯算法一】【经典模版】全排列-编程知识

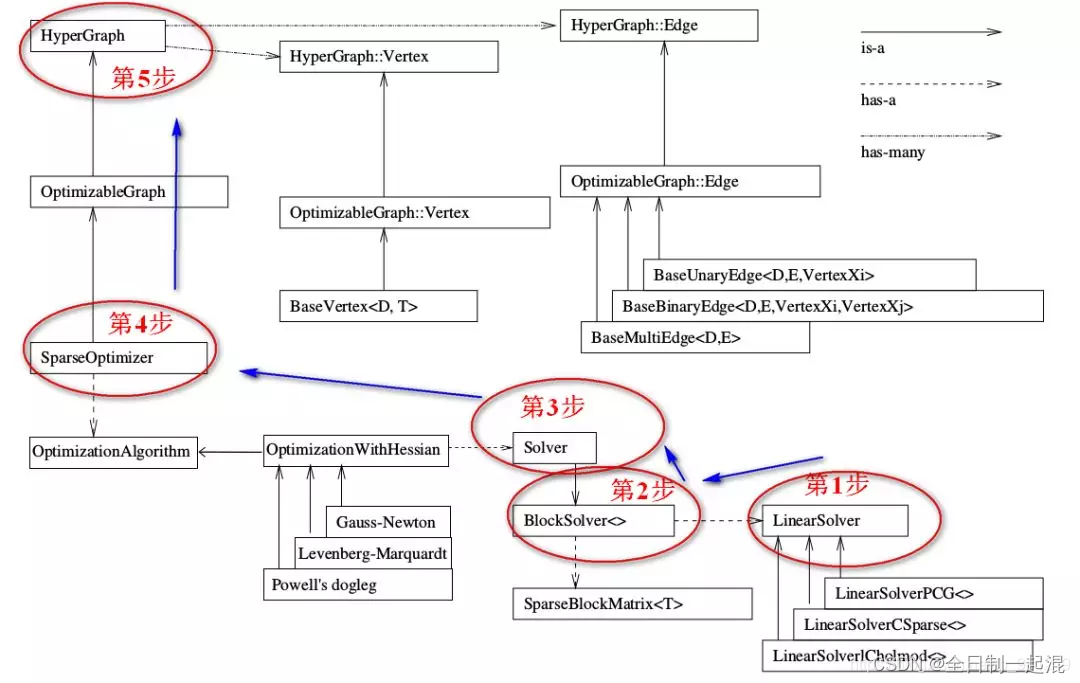
废话不多说，喊一句号子鼓励自己：程序员永不失业，程序员走向架构！本篇Blog的主题是【回溯算法】，使用【数组】这个基本的数据结构来实现，这个高频题的站点是：CodeTop，筛选条件为：目标公司+最近一年+出现频率排序，由高到低的去牛客TOP101去找，只有两个地方都出现过才做这道题（CodeTop本身汇聚了LeetCode的来源），确保刷的题都是高频要面试考的题。
在这里插入图片描述

明确目标题后，附上题目链接，后期可以依据解题思路反复快速练习，题目按照题干的基本数据结构分类，且每个分类的第一篇必定是对基础数据结构的介绍。

全排列【MID】

一道一直想要解决的高频题，理解回溯算法，解决回溯算法经典题目：全排列

题干

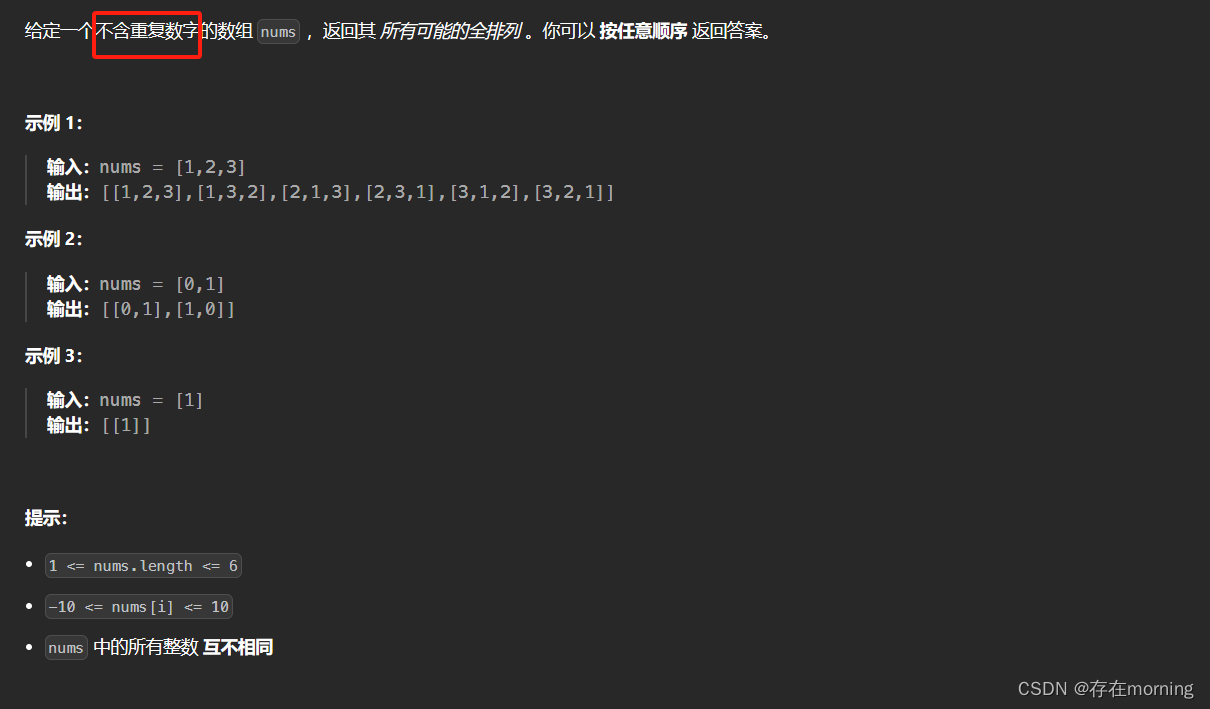
在这里插入图片描述

解题思路

原题解思路地址，我们在高中的时候就做过排列组合的数学题，我们也知道 n 个不重复的数，全排列共有 n! 个。那么我们当时是怎么穷举全排列的呢？比方说给三个数 [1,2,3]，一般是这样：先固定第一位为 1，然后第二位可以是 2，那么第三位只能是 3；然后可以把第二位变成 3，第三位就只能是 2 了；然后就只能变化第一位，变成 2，然后再穷举后两位
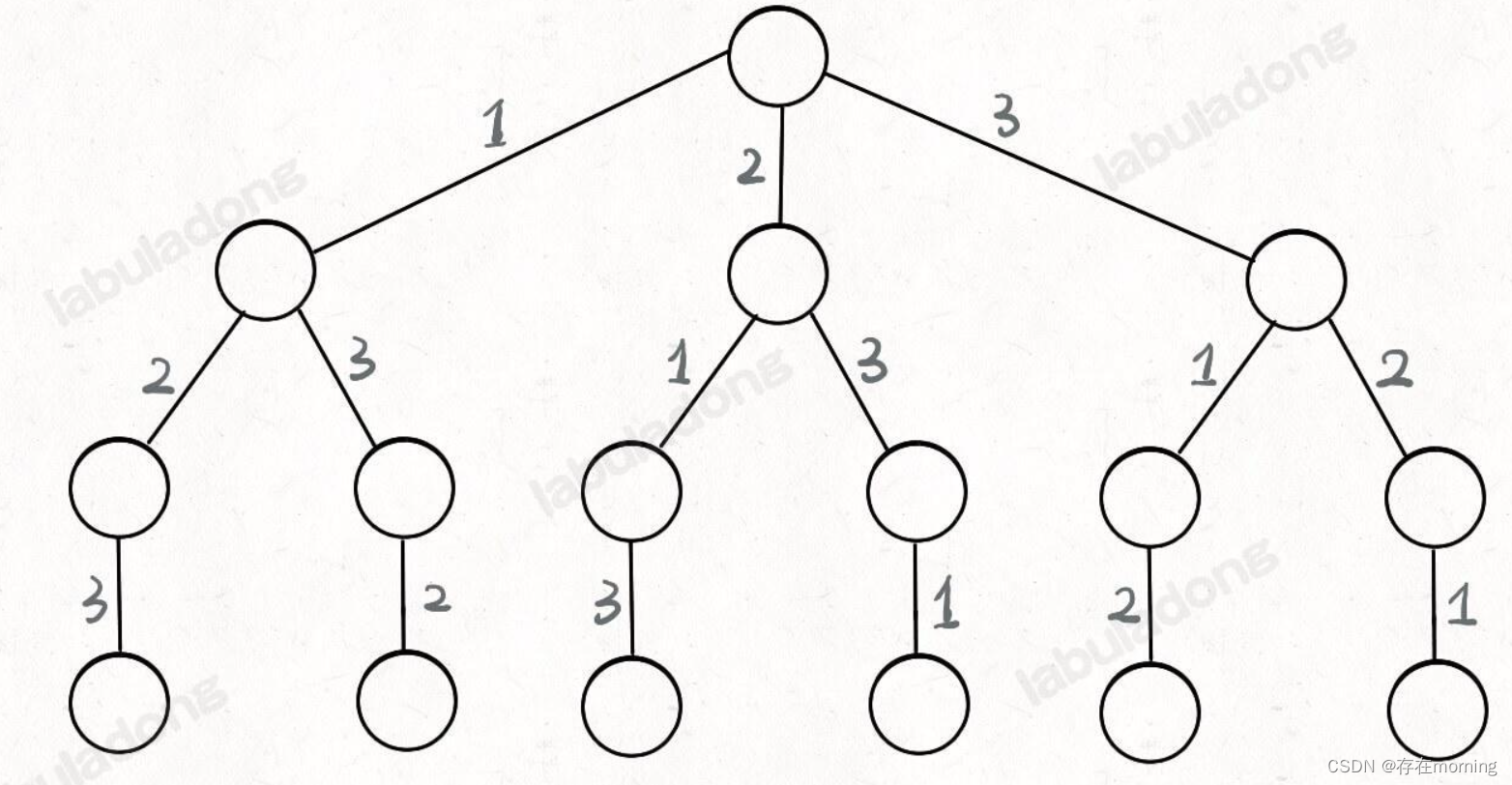
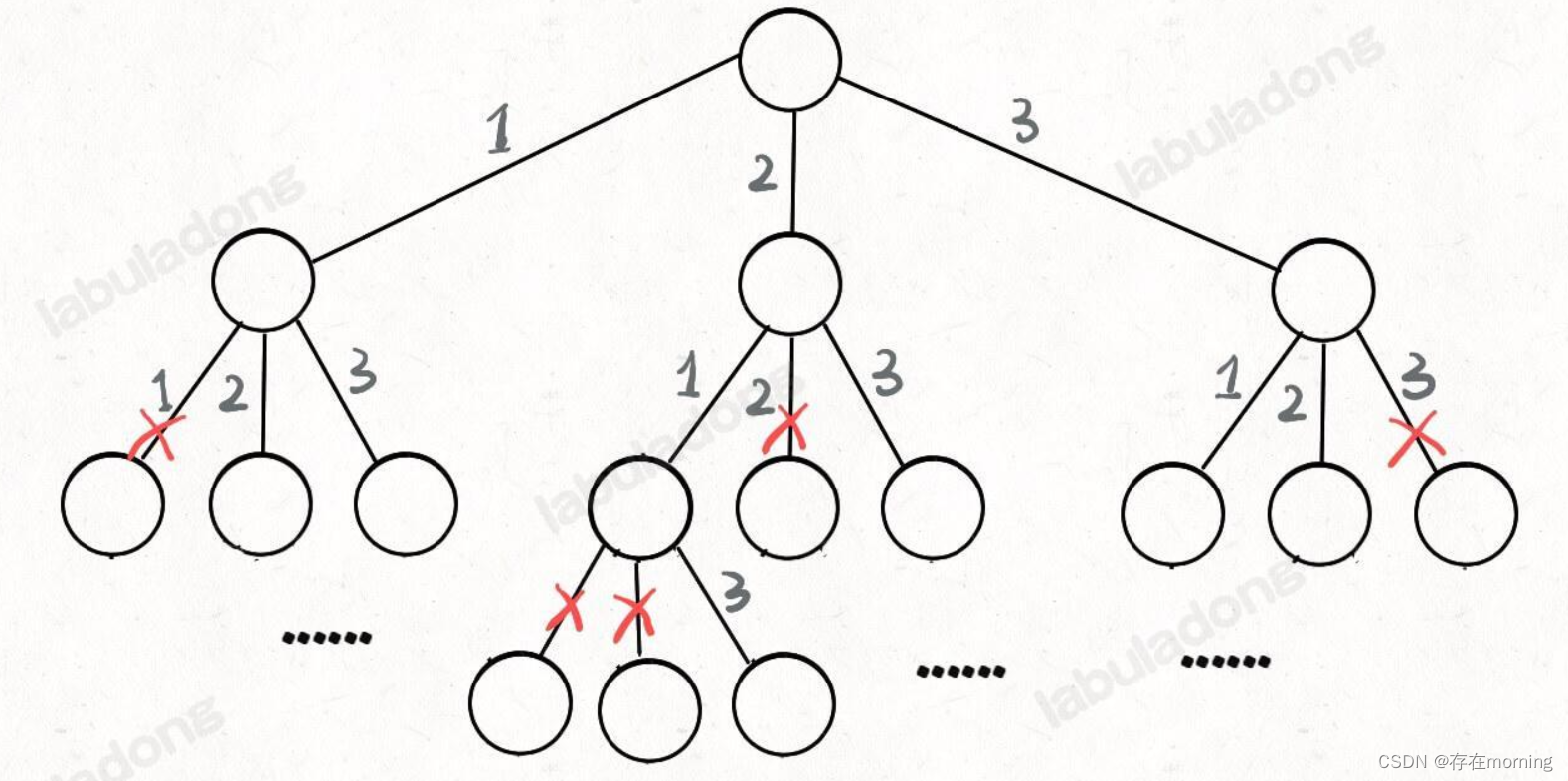
在这里插入图片描述
只要从根遍历这棵树，记录路径上的数字，其实就是所有的全排列。我们不妨把这棵树称为回溯算法的「决策树」。为啥说这是决策树呢，因为你在每个节点上其实都在做决策。比如说你站在下图的红色节点上
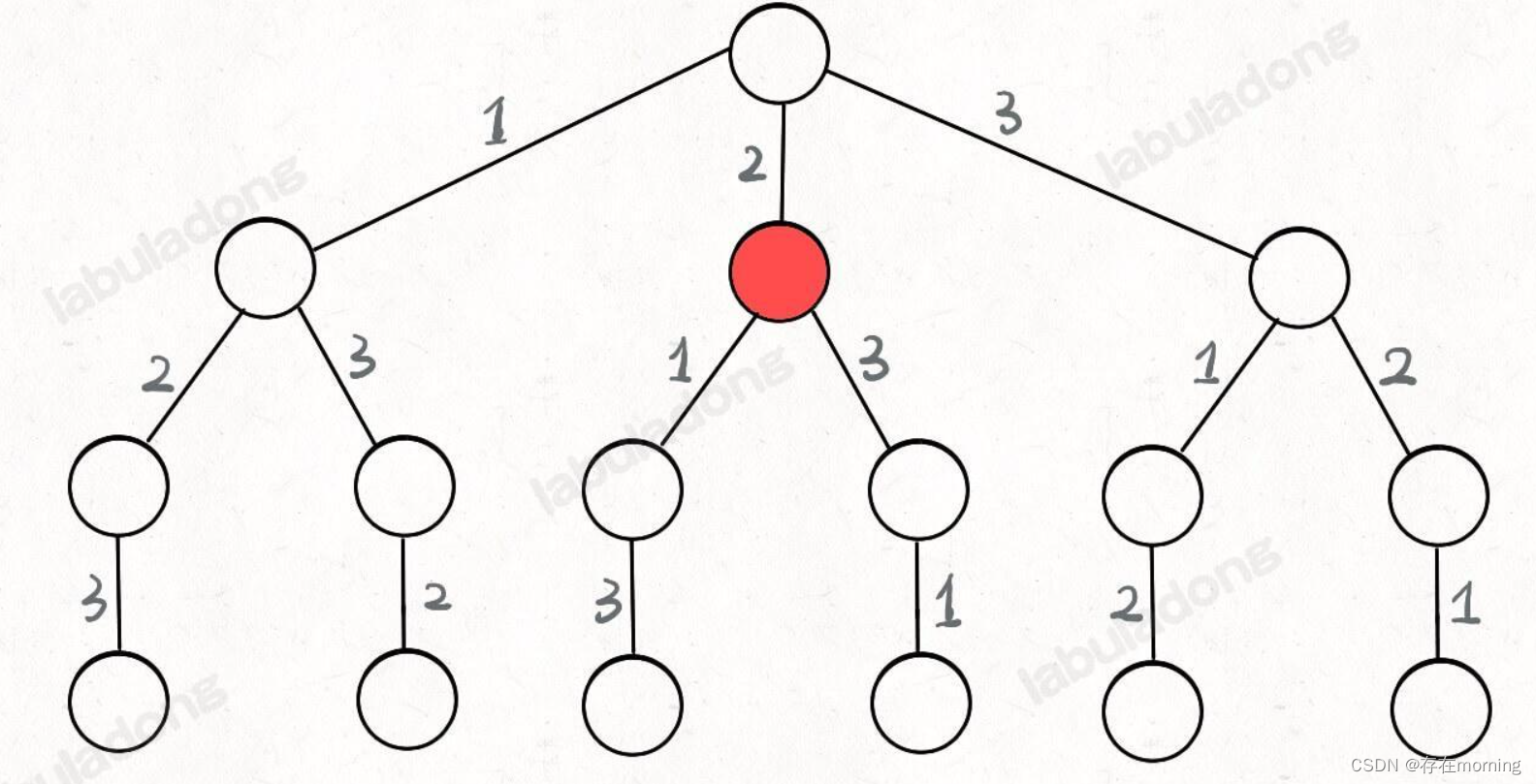
在这里插入图片描述
你现在就在做决策，可以选择 1 那条树枝，也可以选择 3 那条树枝。为啥只能在 1 和 3 之中选择呢？因为 2 这个树枝在你身后，这个选择你之前做过了，而全排列是不允许重复使用数字的。所以[2] 就是「路径」，记录你已经做过的选择；[1,3] 就是「选择列表」，表示你当前可以做出的选择；「结束条件」就是遍历到树的底层叶子节点，这里也就是选择列表为空的时候
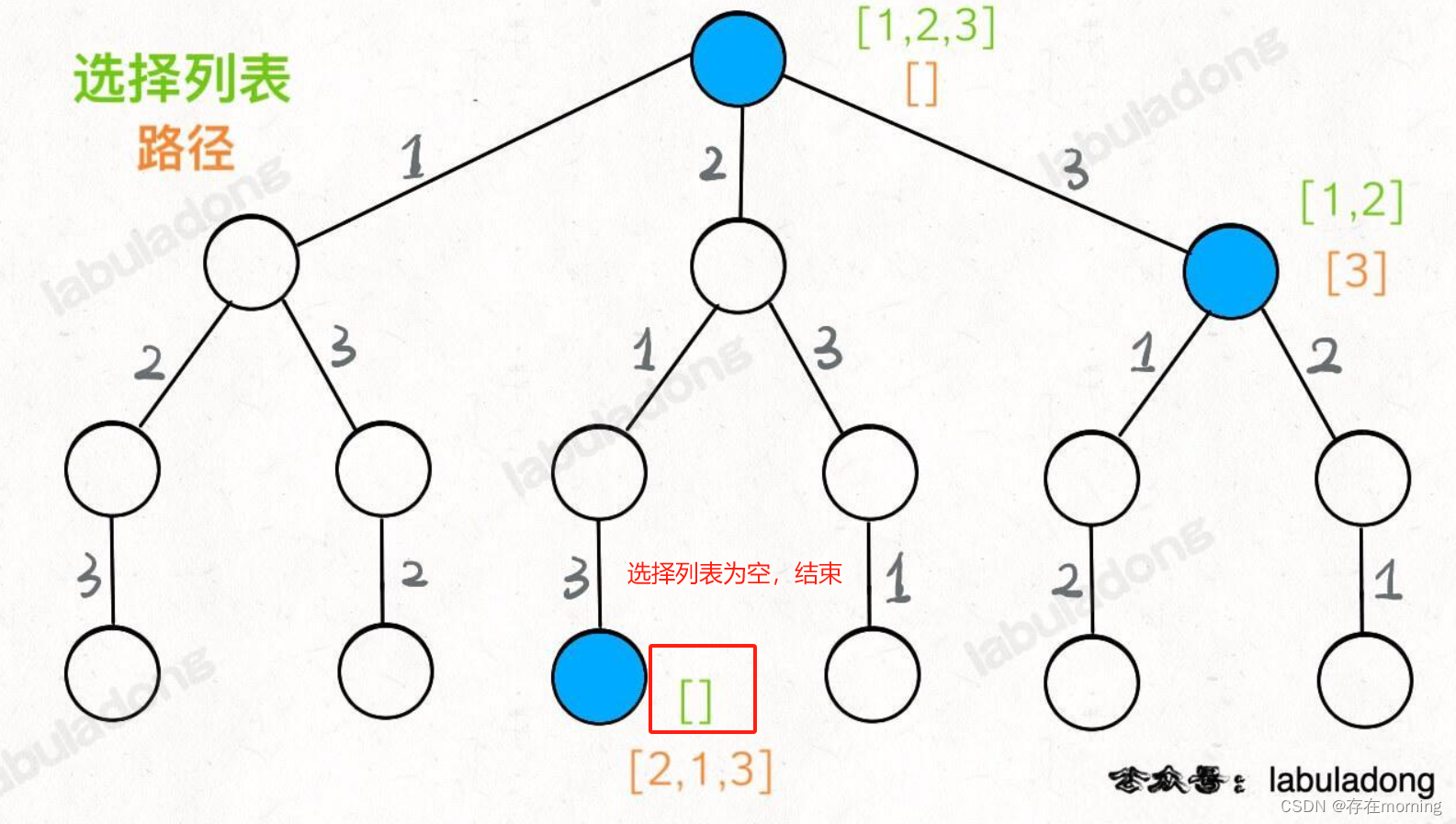
在这里插入图片描述
我们定义的 backtrack 函数其实就像一个指针，在这棵树上游走，同时要正确维护每个节点的属性，每当走到树的底层叶子节点，其「路径」就是一个全排列，「路径」和「选择」是每个节点的属性，函数在树上游走要正确处理节点的属性，那么就要在这两个特殊时间点搞点动作
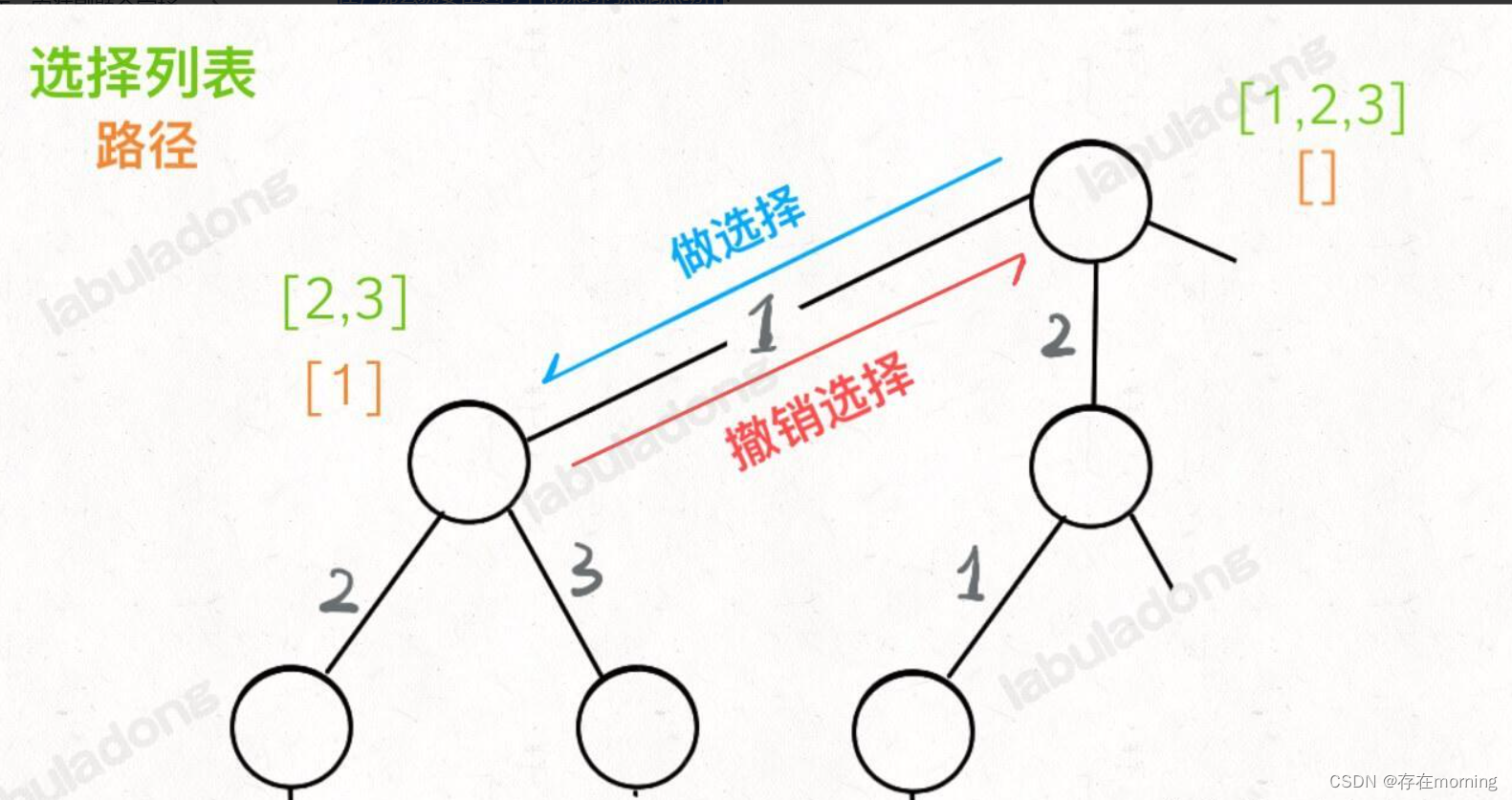
在这里插入图片描述
所以其核心逻辑就是

for 选择 in 选择列表:# 做选择将该选择从选择列表移除路径.add(选择)backtrack(路径, 选择列表)# 撤销选择路径.remove(选择)将该选择再加入选择列表

在这里插入图片描述
符合回溯框架，而且时间复杂度都不可能低于 O(N!)，因为穷举整棵决策树是无法避免的，你最后肯定要穷举出 N! 种全排列结果。这也是回溯算法的一个特点，不像动态规划存在重叠子问题可以优化，回溯算法就是纯暴力穷举，复杂度一般都很高

代码实现

给出代码实现基本档案

基本数据结构：数组
辅助数据结构：无
算法：回溯算法
技巧：无

import java.util.*;public class Solution {// 定义结果集参数private ArrayList<ArrayList<Integer>> result = new ArrayList<ArrayList<Integer>>();/*** 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可*** @param num int整型一维数组* @return int整型ArrayList<ArrayList<>>*/public ArrayList<ArrayList<Integer>> permute (int[] num) {// 1 存储使用标识boolean[] used = new boolean[num.length];// 2 定义路径ArrayList<Integer> path = new ArrayList<Integer>();// 3 回溯寻找路径存储路径,num为选择列表backTrack(num, used, path);return result;}private void backTrack(int[] num, boolean[] used, ArrayList<Integer> path) {// 1 设置结束条件,寻找到叶子节点,补充结果集if (path.size() == num.length) {result.add(new ArrayList<Integer>(path));return;}// 2 遍历选择列表，将选择列表中元素增加到路径列表for (int i = 0; i < num.length; i++) {// 1 已经用过的元素不合法,跳出循环if (used[i] == true) {continue;}// 2 当前元素从选择列表拿出来放到路径列表used[i] = true;path.add(num[i]);// 3 进入下一层选择backTrack(num, used, path);// 4 回溯，将当前元素放回到选择列表，从路径列表移除used[i] = false;path.remove(path.size() - 1);}}
}

复杂度分析

上述代码是一个用于生成整数数组的全排列的回溯算法，下面是对其时间复杂度和空间复杂度的分析：

时间复杂度：

回溯算法的时间复杂度通常取决于递归的深度和每层递归的操作数量。在这个算法中，每层递归都会尝试 num 数组中的每个元素，直到达到终止条件。
在每层递归中，有一个循环来遍历 num 数组的所有元素。由于每个元素都被考虑一次，因此总共有 n 个元素，所以在每层递归中有 O(n) 的操作。
递归的深度取决于 num 数组的大小，也就是 n。在最坏的情况下，递归会深入到 n 层，因此总时间复杂度是 O(n * n!)。

空间复杂度：

空间复杂度主要取决于递归调用的深度，以及用于存储中间结果的数据结构。
递归的深度是 n，因此在调用堆栈中会有最多 n 层递归帧。每个递归帧包括 used 数组和 path 数组，它们的空间复杂度都是 O(n)。
由于存在 n 层递归帧，因此总的空间复杂度为 O(n^2)。

综上所述，上述代码的时间复杂度是 O(n * n!)，其中 n 是输入数组 num 的大小，空间复杂度是 O(n^2)。由于全排列问题的本质，这个时间复杂度是可以接受的，因为全排列的数量本身是 n!，因此生成所有排列的算法必然具有阶乘级的时间复杂度。

拓展知识：回溯算法解题框架

抽象地说，解决一个回溯问题，实际上就是遍历一棵决策树的过程，树的每个叶子节点存放着一个合法答案。你把整棵树遍历一遍，把叶子节点上的答案都收集起来，就能得到所有的合法答案。站在回溯树的一个节点上，你只需要思考 3 个问题：

路径：也就是已经做出的选择。
选择列表：也就是你当前可以做的选择。
结束条件：也就是到达决策树底层，无法再做选择的条件。

回溯算法的框架：

result = []
def backtrack(路径, 选择列表):if 满足结束条件:result.add(路径)returnfor 选择 in 选择列表:做选择backtrack(路径, 选择列表)撤销选择

其核心就是 for 循环里面的递归，在递归调用之前「做选择」，在递归调用之后「撤销选择」