手撕视觉slam14讲 ch7 / pose_estimation_3d2d.cpp （2）-编程知识

上一篇文章中: 手撕ch7/pose_estimation_3d2d（1），我们调用了epnp的方法进行位姿估计，这里我们使用非线性优化的方法来求解位姿，使用g2o进行BA优化

首先介绍g2o：可参考：g2o详细介绍

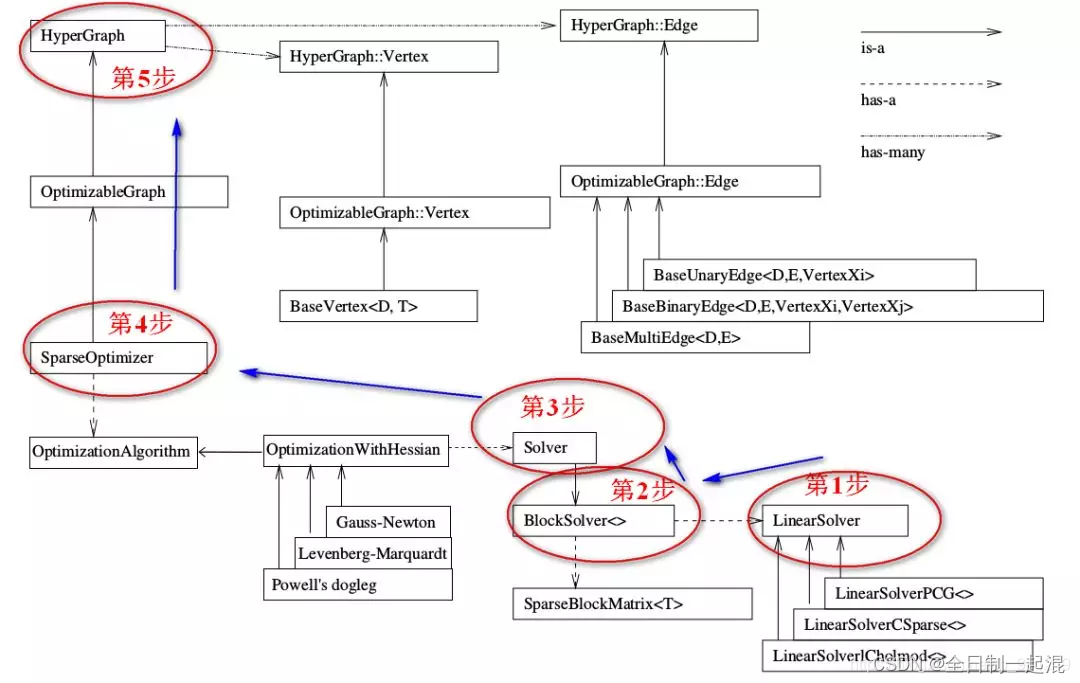
1.构建g2o图优化思路：

步骤一：创建线性方程求解器，确定分解方法

// 每个误差项优化变量维度为3，误差值维度为1
typedef g2o::BlockSolver< g2o::BlockSolverTraits<3,1> > Block;  
// 创建一个线性求解器 LinearSolver，采用 dense cholesky 分解法
Block::LinearSolverType* linearSolver = new g2o::LinearSolverDense<Block::PoseMatrixType>();

步骤二：构造线性方程的矩阵块，并用上面定义的线性求解器初始化

Block* solver_ptr = new Block( linearSolver );

BlockSolver 内部包含 LinearSolver，用上面定义的线性求解器 LinearSolver 来初始化，前面已经给定了优化变量的维度；

步骤三：创建总求解器 solver，并从 GN, LM, DogLeg 中选一个，再用上述块求解器 BlockSolver 初始化

g2o::OptimizationAlgorithmLevenberg* solver = new g2o::OptimizationAlgorithmLevenberg( solver_ptr );

步骤四：创建稀疏优化器（SparseOptimizer）

g2o::SparseOptimizer optimizer;     // 图模型
optimizer.setAlgorithm( solver );   // 用前面定义好的求解器作为求解方法：
optimizer.setVerbose( true );       // 打开调试输出

步骤五：定义图的顶点和边，并添加到 SparseOptimizer 优化器中

// 创建一个顶点
CurveFittingVertex* v = new CurveFittingVertex(); 
// 初始化顶点的值
v->setEstimate( Eigen::Vector3d(0,0,0) );
// 设置顶点的编号
v->setId(0);
// 向图中添加顶点
optimizer.addVertex( v );for ( int i=0; i<N; i++ )    // 往图中增加边
{// 创建一条边CurveFittingEdge* edge = new CurveFittingEdge( x_data[i] );// 设置边的 idedge->setId(i);// 设置边连接的顶点edge->setVertex( 0, v );                // 设置观测数值edge->setMeasurement( y_data[i] );      // 设置信息矩阵：协方差矩阵之逆edge->setInformation( Eigen::Matrix<double,1,1>::Identity()*1/(w_sigma*w_sigma) ); // 将边添加到图中optimizer.addEdge( edge );
}

步骤六：设置优化参数，开始执行优化

optimizer.initializeOptimization();
optimizer.optimize(100); // 迭代次数

对应原文完整代码如下：

void bundleAdjustmentG2O(const VecVector3d &points_3d,const VecVector2d &points_2d,const Mat &K,Sophus::SE3d &pose) {// 步骤一：构建图优化，先设定g2otypedef g2o::BlockSolver<g2o::BlockSolverTraits<6, 3>> BlockSolverType;  // pose is 6, landmark is 3//步骤二： 线性求解器类型typedef g2o::LinearSolverDense<BlockSolverType::PoseMatrixType> LinearSolverType; //步骤三： 梯度下降方法，可以从GN, LM, DogLeg 中选auto solver = new g2o::OptimizationAlgorithmGaussNewton(g2o::make_unique<BlockSolverType>(g2o::make_unique<LinearSolverType>()));//步骤四： 创建稀疏优化器g2o::SparseOptimizer optimizer;     // 图模型optimizer.setAlgorithm(solver);   // 设置求解器optimizer.setVerbose(true);       // 打开调试输出//步骤五： 定义图的顶点和边// vertex 定义顶点VertexPose *vertex_pose = new VertexPose(); // 定义 相机位姿 为顶点vertex_pose->setId(0);// 设置顶点的编号vertex_pose->setEstimate(Sophus::SE3d());// 初始化顶点的值optimizer.addVertex(vertex_pose);// 向图中添加顶点// K 相机内参Eigen::Matrix3d K_eigen;K_eigen <<K.at<double>(0, 0), K.at<double>(0, 1), K.at<double>(0, 2),K.at<double>(1, 0), K.at<double>(1, 1), K.at<double>(1, 2),K.at<double>(2, 0), K.at<double>(2, 1), K.at<double>(2, 2);// edges 定义 边int index = 1;// 往图中增加边for (size_t i = 0; i < points_2d.size(); ++i) {auto p2d = points_2d[i];auto p3d = points_3d[i];EdgeProjection *edge = new EdgeProjection(p3d, K_eigen);// 创建一条边edge->setId(index);// 设置边的 idedge->setVertex(0, vertex_pose);// 设置边连接的顶点edge->setMeasurement(p2d);  // 设置观测数值edge->setInformation(Eigen::Matrix2d::Identity());// 设置信息矩阵：协方差矩阵之逆optimizer.addEdge(edge);// 将边添加到图中index++;}//步骤六：设置优化参数，开始优化chrono::steady_clock::time_point t1 = chrono::steady_clock::now();optimizer.setVerbose(true);optimizer.initializeOptimization();// 设置优化初始值optimizer.optimize(10);// 迭代次数chrono::steady_clock::time_point t2 = chrono::steady_clock::now();chrono::duration<double> time_used = chrono::duration_cast<chrono::duration<double>>(t2 - t1);cout << "optimization costs time: " << time_used.count() << " seconds." << endl;cout << "pose estimated by g2o =\n" << vertex_pose->estimate().matrix() << endl;pose = vertex_pose->estimate();
}

其中我们需要关注如何定义顶点（Vertex）和边（edge）

2. 顶点（Vertex）：

g2o 提供了一个比较通用的适合大多数情况的模板类 BaseVertex<D, T>，其中D 是 int 类型，表示顶点 Vertex 的最小维度，比如 3D 空间中旋转是 3 维的，那么这里 D=3；
但是在源码注释中说 D 并非是顶点（更确切的说是状态变量）的维度，而是其在流形空间（manifold）的最小表示(SO3->so3,SE3->se3).

T 是待估计 Vertex 的数据类型，比如用四元数表达三维旋转的话，T 就是 Quaternion 类型

我们自定义一个顶点需要重写以下函数

class myVertex: public g2::BaseVertex<Dim, Type>
{
public:// 类成员变量如果是固定大小对象需要加上以下的宏定义EIGEN_MAKE_ALIGNED_OPERATOR_NEW// 构造函数myVertex(){}// 读写函数virtual void read(std::istream& is) {}virtual void write(std::ostream& os) const {}// 重置函数virtual void setOriginImpl(){_estimate = Type();}// 更新函数virtual void oplusImpl(const double* update) override{_estimate += /*update*/;}
}

对应原文代码：

class VertexPose : public g2o::BaseVertex<6, Sophus::SE3d> { //优化变量是 6 自由度的李代数
public:EIGEN_MAKE_ALIGNED_OPERATOR_NEW;//重置，设定被优化变量的原始值virtual void setToOriginImpl() override {_estimate = Sophus::SE3d();}/// left multiplication on SE3 //更新virtual void oplusImpl(const double *update) override {Eigen::Matrix<double, 6, 1> update_eigen;update_eigen << update[0], update[1], update[2], update[3], update[4], update[5];_estimate = Sophus::SE3d::exp(update_eigen) * _estimate;  // 左乘更新 SE3 - 旋转矩阵R}virtual bool read(istream &in) override {} //存盘virtual bool write(ostream &out) const override {}//读盘
};

3. 边（edge）

我们一般使用的类是 BaseUnaryEdge，BaseBinaryEdge，BaseMultiEdge 分别表示一元边，两元边，多元边（位于 g2o/g2o/core/base_edge.h 中），类似于顶点，他们又继承自OptimizableGraph::Edge （位于 g2o/g2o/core/optimizable_graph.h 中），hyper_graph::Edge（位于g2o/g2o/core/hyper_graph.h 中）

一元边表示只连接一个顶点，二元边表示连接两个顶点，多元边表示连接 3 个或以上顶点。

主要参数有：D, E, VertexXi, VertexXj

D 是 int 型，表示测量值的维度；
E 表示测量值的数据类型；
VertexXi，VertexXj 分别表示不同顶点的类型。

自定义边需要重写以下成员函数：最重要的是误差计算函数computeError()，计算雅克比矩阵linearizeOplus() 两个函数

class myEdge: public g2o::BaseBinaryEdge<errorDim, errorType, Vertex1Type, Vertex2Type>
{public:EIGEN_MAKE_ALIGNED_OPERATOR_NEW      myEdge(){}     // 读写函数virtual bool read(istream& in) {}virtual bool write(ostream& out) const {}  // 误差计算函数virtual void computeError() override{// ..._error = _measurement - Something;}      // 计算雅克比矩阵 virtual void linearizeOplus() override{_jacobianOplusXi(pos, pos) = something;// ...         /*_jocobianOplusXj(pos, pos) = something;...*/}      private:// data
}

对应原文代码：

// 仅估计位姿的一元边
class EdgeProjection : public g2o::BaseUnaryEdge<2, Eigen::Vector2d, VertexPose> {
public:EIGEN_MAKE_ALIGNED_OPERATOR_NEW;//构造函数EdgeProjection(const Eigen::Vector3d &pos, const Eigen::Matrix3d &K) : _pos3d(pos), _K(K) {}// 误差计算函数virtual void computeError() override {const VertexPose *v = static_cast<VertexPose *> (_vertices[0]);Sophus::SE3d T = v->estimate();Eigen::Vector3d pos_pixel = _K * (T * _pos3d);//将3D世界坐标转为相机像素坐标pos_pixel /= pos_pixel[2];_error = _measurement - pos_pixel.head<2>(); //误差=测量值-投影得到的值}// 计算雅克比矩阵 virtual void linearizeOplus() override {const VertexPose *v = static_cast<VertexPose *> (_vertices[0]);Sophus::SE3d T = v->estimate();Eigen::Vector3d pos_cam = T * _pos3d;//相机坐标系下空间点的坐标=相机位姿 * 空间点的坐标double fx = _K(0, 0);double fy = _K(1, 1);double cx = _K(0, 2);double cy = _K(1, 2);double X = pos_cam[0];double Y = pos_cam[1];double Z = pos_cam[2];double Z2 = Z * Z;// 2*6的雅克比矩阵_jacobianOplusXi<< -fx / Z, 0, fx * X / Z2, fx * X * Y / Z2, -fx - fx * X * X / Z2, fx * Y / Z,0, -fy / Z, fy * Y / (Z * Z), fy + fy * Y * Y / Z2, -fy * X * Y / Z2, -fy * X / Z;}//读写操作virtual bool read(istream &in) override {}virtual bool write(ostream &out) const override {}private:Eigen::Vector3d _pos3d;Eigen::Matrix3d _K;
};