SpringBoot集成Activiti7
SpringBoot版本使用2.7.16
<parent><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-parent</artifactId><version>2.7.16</version><relativePath/> <!-- lookup parent from repository -->
</parent>
导入数据库及activiti相关依赖
<dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter</artifactId>
</dependency>
<dependency><groupId>mysql</groupId><artifactId>mysql-connector-java</artifactId><version>8.0.23</version>
</dependency>
<dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-jdbc</artifactId>
</dependency>
<dependency><groupId>org.activiti</groupId><artifactId>activiti-spring-boot-starter</artifactId><version>7.1.0.M6</version>
</dependency>
activiti-spring-boot-starter默认集成Spring Security,此处先禁用
import org.activiti.core.common.spring.identity.config.ActivitiSpringIdentityAutoConfiguration;
import org.springframework.boot.SpringApplication;
import org.springframework.boot.autoconfigure.SpringBootApplication;@SpringBootApplication(exclude = {ActivitiSpringIdentityAutoConfiguration.class})
public class ActivitiApplication {public static void main(String[] args) {SpringApplication.run(ActivitiApplication.class, args);}}添加UserGroupManager配置
import org.activiti.api.runtime.shared.identity.UserGroupManager;
import org.springframework.context.annotation.Bean;
import org.springframework.context.annotation.Configuration;import java.util.ArrayList;
import java.util.List;@Configuration
public class ActivitiConfiguration {@Beanpublic UserGroupManager userGroupManager() {return new UserGroupManager() {@Overridepublic List<String> getUserGroups(String s) {return new ArrayList<>();}@Overridepublic List<String> getUserRoles(String s) {return null;}@Overridepublic List<String> getGroups() {return null;}@Overridepublic List<String> getUsers() {return null;}};}
}
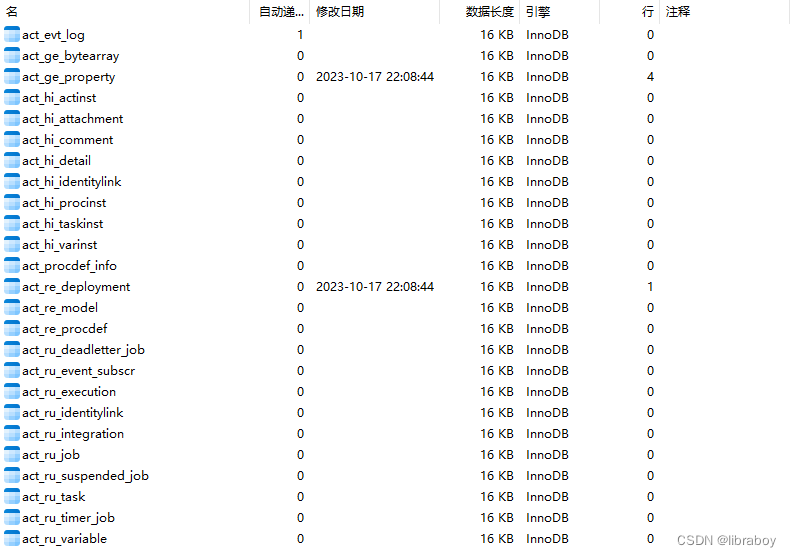
启动服务,MySQL中生成25张表。