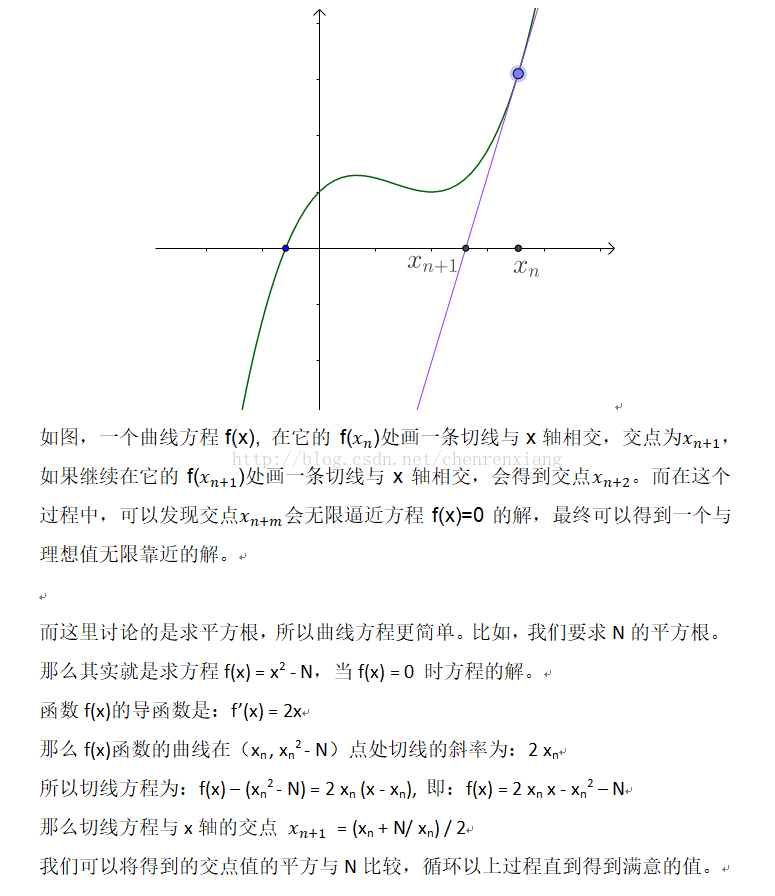
Go-Python-Java-C-LeetCode高分解法-第十周合集

前言

本题解Go语言部分基于 LeetCode-Go
其他部分基于本人实践学习
个人题解GitHub连接：LeetCode-Go-Python-Java-C
欢迎订阅CSDN专栏，每日一题，和博主一起进步
LeetCode专栏
我搜集到了50道精选题，适合速成概览大部分常用算法
突破算法迷宫：精选50道-算法刷题指南

在这里插入图片描述

本文部分内容来自网上搜集与个人实践。如果任何信息存在错误,欢迎读者批评指正。本文仅用于学习交流,不用作任何商业用途。

64. Minimum Path Sum

题目

Given a m x n grid filled with non-negative numbers, find a path from top left to bottom right which minimizes the sum of all numbers along its path.

Note: You can only move either down or right at any point in time.

Example:

Input:
[[1,3,1],[1,5,1],[4,2,1]
]
Output: 7
Explanation: Because the path 1→3→1→1→1 minimizes the sum.

题目大意

给定一个包含非负整数的 m x n 网格，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。说明：每次只能向下或者向右移动一步。

解题思路

  • 在地图上求出从左上角到右下角的路径中，数字之和最小的一个，输出数字和。
  • 这一题最简单的想法就是用一个二维数组来 DP，当然这是最原始的做法。由于只能往下和往右走，只需要维护 2 列信息就可以了，从左边推到最右边即可得到最小的解。更近一步，可以直接在原来的数组中做原地 DP，空间复杂度为 0 。
    以下是每个版本的解题思路的详细介绍：

Go 版本解题思路

  1. 首先，获取网格的行数 m 和列数 n。

  2. 创建一个一维数组 dp，用于存储从起点到每个位置的最小路径和。将 dp[0] 初始化为起点的值，即 grid[0][0]。

  3. 遍历第一行，计算每个位置的最小路径和并存储在 dp 数组中。这是因为只能向右移动，所以第一行的最小路径和只能从左向右递增。

  4. 遍历剩余的行和列：

    • 如果当前位置是第一列，只能从上方移动到达，因此更新 dp[0] 的值。
    • 如果当前位置不是第一列，计算从上方和左方两个方向到达当前位置的最小路径和，并更新 dp 数组的值。

  5. 最后一个元素 dp[n-1] 存储了从起点到终点的最小路径和，返回它作为最终答案。

Python 版本解题思路

  1. 获取网格的行数 m 和列数 n。

  2. 创建一个二维数组 dp，用于存储从起点到每个位置的最小路径和。将 dp[0][0] 初始化为起点的值，即 grid[0][0]。

  3. 初始化 dp 数组的第一行和第一列，分别表示从起点出发到达第一行和第一列各个位置的最小路径和。这是因为只能向右或向下移动，所以第一行和第一列的最小路径和只能递增。

  4. 遍历剩余的行和列：

    • 对于位置 (i, j)，计算从上方 (i-1, j) 和左方 (i, j-1) 到达当前位置的最小路径和，然后将最小值与当前位置的值相加，更新 dp[i][j]。

  5. 最后一个元素 dp[m-1][n-1] 存储了从起点到终点的最小路径和，返回它作为最终答案。

Java 版本解题思路

  1. 获取网格的行数 m 和列数 n。

  2. 创建一个二维数组 dp，用于存储从起点到每个位置的最小路径和。将 dp[0][0] 初始化为起点的值，即 grid[0][0]。

  3. 初始化 dp 数组的第一行和第一列，分别表示从起点出发到达第一行和第一列各个位置的最小路径和。这是因为只能向右或向下移动，所以第一行和第一列的最小路径和只能递增。

  4. 使用嵌套的 for 循环遍历剩余的行和列：

    • 对于位置 (i, j)，计算从上方 (i-1, j) 和左方 (i, j-1) 到达当前位置的最小路径和，然后将最小值与当前位置的值相加，更新 dp[i][j]。

  5. 最后一个元素 dp[m-1][n-1] 存储了从起点到终点的最小路径和，返回它作为最终答案。

C++ 版本解题思路

  1. 获取网格的行数 m 和列数 n。

  2. 创建一个二维数组 dp，用于存储从起点到每个位置的最小路径和。将 dp[0][0] 初始化为起点的值，即 grid[0][0]。

  3. 初始化 dp 数组的第一行和第一列，分别表示从起点出发到达第一行和第一列各个位置的最小路径和。这是因为只能向右或向下移动，所以第一行和第一列的最小路径和只能递增。

  4. 使用嵌套的 for 循环遍历剩余的行和列：

    • 对于位置 (i, j)，计算从上方 (i-1, j) 和左方 (i, j-1) 到达当前位置的最小路径和，然后将最小值与当前位置的值相加，更新 dp[i][j]。

  5. 最后一个元素 dp[m-1][n-1] 存储了从起点到终点的最小路径和，返回它作为最终答案。

无论使用哪种编程语言，上述解题思路的核心思想都是利用动态规划，从左上角开始逐步计算并更新到达每个位置的最小路径和，最终得到最小路径和的答案。

代码

Go

// 定义一个函数minPathSum，它接受一个二维整数网格grid作为参数，返回最小路径和的整数。
func minPathSum(grid [][]int) int {// 获取网格的行数mm := len(grid)// 如果网格行数为0，直接返回0if m == 0 {return 0}// 获取网格的列数nn := len(grid[0])// 创建一个一维数组dp，用于存储从起点到每个位置的最小路径和dp := make([]int, n)// 初始化dp数组的第一个元素为起点的值dp[0] = grid[0][0]// 遍历第一行，计算每个位置的最小路径和并存储在dp数组中for i := 1; i < n; i++ {dp[i] = grid[0][i] + dp[i-1]}// 遍历剩余行for i := 1; i < m; i++ {for j := 0; j < n; j++ {if j == 0 {// 如果当前位置是第一列，只能从上方移动到达，更新dp数组的值dp[0] = dp[0] + grid[i][0]continue}// 如果当前位置不是第一列，计算从上方和左方两个方向到达当前位置的最小路径和，并更新dp数组的值dp[j] = min(dp[j-1], dp[j]) + grid[i][j]}}// 最后一个元素dp[n-1]存储了从起点到终点的最小路径和，返回它return dp[n-1]
}// 定义一个辅助函数min，用于比较两个整数的大小并返回较小的那个整数。
func min(a, b int) int {if a < b {return a}return b
}

Python

class Solution:def minPathSum(self, grid: List[List[int]]) -> int:# 获取网格的行数m和列数nm = len(grid)n = len(grid[0])# 创建一个二维数组dp，用于存储从起点到每个位置的最小路径和dp = [[0] * n for _ in range(m)]# 初始化dp数组的第一个元素为起点的值dp[0][0] = grid[0][0]# 初始化第一行和第一列的最小路径和for i in range(1, m):dp[i][0] = dp[i-1][0] + grid[i][0]for j in range(1, n):dp[0][j] = dp[0][j-1] + grid[0][j]# 遍历剩余网格，计算每个位置的最小路径和for i in range(1, m):for j in range(1, n):dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + grid[i][j]# 返回终点的最小路径和return dp[m-1][n-1]

Java

class Solution {public int minPathSum(int[][] grid) {// 获取网格的行数m和列数nint m = grid.length;int n = grid[0].length;// 创建一个二维数组dp，用于存储从起点到每个位置的最小路径和int[][] dp = new int[m][n];// 初始化dp数组的第一个元素为起点的值dp[0][0] = grid[0][0];// 初始化第一行和第一列的最小路径和for (int i = 1; i < m; i++) {dp[i][0] = dp[i-1][0] + grid[i][0];}for (int j = 1; j < n; j++) {dp[0][j] = dp[0][j-1] + grid[0][j];}// 遍历剩余网格，计算每个位置的最小路径和for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {dp[i][j] = Math.min(dp[i-1][j], dp[i][j-1]) + grid[i][j];}}// 返回终点的最小路径和return dp[m-1][n-1];}
}

Cpp

class Solution {
public:int minPathSum(vector<vector<int>>& grid) {// 获取网格的行数m和列数nint m = grid.size();int n = grid[0].size();// 创建一个二维数组dp，用于存储从起点到每个位置的最小路径和vector<vector<int>> dp(m, vector<int>(n, 0));// 初始化dp数组的第一个元素为起点的值dp[0][0] = grid[0][0];// 初始化第一行和第一列的最小路径和for (int i = 1; i < m; i++) {dp[i][0] = dp[i-1][0] + grid[i][0];}for (int j = 1; j < n; j++) {dp[0][j] = dp[0][j-1] + grid[0][j];}// 遍历剩余网格，计算每个位置的最小路径和for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + grid[i][j];}}// 返回终点的最小路径和return dp[m-1][n-1];}
};

好的，让我为每个版本的代码提供更详细的基础知识解释。

Go 版本解释

这是 Go 语言版本的解决方案，需要掌握以下基础知识：

  1. 切片 (Slices)：Go 中的切片是可变长度的序列，通常用于处理动态数组。在这个解决方案中，我们使用切片来存储 dp 数组。

  2. 循环 (Loops)：在 Go 中，通常使用 for 循环来迭代数组或切片的元素。在这个解决方案中，我们使用 for 循环来遍历二维数组，计算最小路径和。

  3. 条件语句 (Conditional Statements)：Go 中的条件语句（如 if 语句）用于根据条件执行不同的代码块。在这个解决方案中，我们使用条件语句来处理特殊情况，例如处理第一行和第一列的元素。

  4. 函数 (Functions)：在 Go 中，函数是可以独立调用的代码块。在这个解决方案中，我们定义了一个用于计算最小路径和的函数 minPathSum。

Python 版本解释

这是 Python 版本的解决方案，需要掌握以下基础知识：

  1. 列表 (Lists)：在 Python 中，列表是可变的有序序列，通常用于存储多个值。在这个解决方案中，我们使用列表来表示 dp 数组。

  2. 循环 (Loops)：Python 使用 for 循环来遍历列表、数组或其他可迭代对象的元素。在这个解决方案中，我们使用 for 循环来遍历二维数组，并计算最小路径和。

  3. 条件语句 (Conditional Statements)：Python 中的条件语句（如 if 语句）用于根据条件执行不同的代码块。在这个解决方案中，我们使用条件语句来处理特殊情况，例如处理第一行和第一列的元素。

  4. 类 (Classes)：在这个解决方案中，我们使用了类来定义 Solution 类，其中包含了计算最小路径和的方法 minPathSum。这是一种面向对象的编程方式。

Java 版本解释

这是 Java 版本的解决方案，需要掌握以下基础知识：

  1. 数组 (Arrays)：Java 中的数组是固定大小的数据结构，用于存储多个相同类型的元素。在这个解决方案中，我们使用二维数组来表示 grid 和 dp 数组。

  2. 循环 (Loops)：Java 使用 for 循环来遍历数组或集合中的元素。在这个解决方案中，我们使用嵌套的 for 循环来遍历二维数组，并计算最小路径和。

  3. 条件语句 (Conditional Statements)：Java 中的条件语句（如 if 语句）用于根据条件执行不同的代码块。在这个解决方案中，我们使用条件语句来处理特殊情况，例如处理第一行和第一列的元素。

  4. 类 (Classes)：在这个解决方案中，我们使用了类来定义 Solution 类，其中包含了计算最小路径和的方法 minPathSum。这是一种面向对象的编程方式。

C++ 版本解释

这是 C++ 版本的解决方案，需要掌握以下基础知识：

  1. 数组 (Arrays)：C++ 中的数组是固定大小的数据结构，用于存储多个相同类型的元素。在这个解决方案中，我们使用二维数组来表示 grid 和 dp 数组。

  2. 循环 (Loops)：C++ 使用 for 循环来遍历数组或集合中的元素。在这个解决方案中，我们使用嵌套的 for 循环来遍历二维数组，并计算最小路径和。

  3. 条件语句 (Conditional Statements)：C++ 中的条件语句（如 if 语句）用于根据条件执行不同的代码块。在这个解决方案中，我们使用条件语句来处理特殊情况，例如处理第一行和第一列的元素。

  4. 类 (Classes)：在这个解决方案中，我们没有使用类，而是直接定义了一个全局的 Solution 函数，其中包含了计算最小路径和的代码。

总之，无论使用哪种编程语言，理解和掌握数组、循环、条件语句和函数/类的基本概念是解决这个问题的关键。此外，了解动态规划的基本原理也对理解这些解决方案非常有帮助。

65. Valid Number

题目

A valid number can be split up into these components (in order):

  1. A decimal number or an integer.
  2. (Optional) An ‘e’ or ‘E’, followed by an integer.

A decimal number can be split up into these components (in order):

  1. (Optional) A sign character (either ‘+’ or ‘-’).
  2. One of the following formats:
    1. One or more digits, followed by a dot ‘.’.
    2. One or more digits, followed by a dot ‘.’, followed by one or more digits.
    3. A dot ‘.’, followed by one or more digits.

An integer can be split up into these components (in order):

  1. (Optional) A sign character (either ‘+’ or ‘-’).
  2. One or more digits.

For example, all the following are valid numbers: ["2", "0089", "-0.1", "+3.14", "4.", "-.9", "2e10", "-90E3", "3e+7", "+6e-1", "53.5e93", "-123.456e789"], while the following are not valid numbers: ["abc", "1a", "1e", "e3", "99e2.5", "--6", "-+3", "95a54e53"].

Given a string s, return true if s is a valid number.

Example:

Input: s = "0"
Output: trueInput: s = "e"
Output: false

题目大意

给定一个字符串S，请根据以上的规则判断该字符串是否是一个有效的数字字符串。

解题思路

  • 用三个变量分别标记是否出现过数字、是否出现过’.'和 是否出现过 ‘e/E’
  • 从左到右依次遍历字符串中的每一个元素
    • 如果是数字，则标记数字出现过
    • 如果是 ‘.’, 则需要 '.'没有出现过，并且 ‘e/E’ 没有出现过，才会进行标记
    • 如果是 ‘e/E’, 则需要 'e/E’没有出现过，并且前面出现过数字，才会进行标记
    • 如果是 ‘+/-’, 则需要是第一个字符，或者前一个字符是 ‘e/E’，才会进行标记，并重置数字出现的标识
    • 最后返回时，需要字符串中至少出现过数字，避免下列case: s == ‘.’ or ‘e/E’ or ‘+/e’ and etc…
      好的，让我再详细介绍每个版本的解题思路：

Go 版本解题思路

  1. 标志位设置： 用三个布尔型变量 numFlag、dotFlag、eFlag 分别标记是否出现过数字、是否出现过小数点、是否出现过指数符号。

  2. 遍历字符串： 从左到右遍历字符串的每个字符。

  3. 条件判断：

    • 如果是数字，将 numFlag 置为 true。
    • 如果是小数点，需要确保小数点之前未出现过，并且指数符号未出现过，然后将 dotFlag 置为 true。
    • 如果是指数符号，需要确保指数符号之前未出现过，并且之前出现过数字，然后将 eFlag 置为 true，并重置 numFlag。
    • 如果是正负号，需要是第一个字符，或者前一个字符是指数符号，然后进行标记，并重置数字出现的标识 numFlag。
    • 如果是其他字符，返回 false。

  4. 返回结果： 最后需要确保字符串中至少出现过数字，以避免类似字符串为 “.” 或 “e” 的特殊情况。

Python 版本解题思路

  1. 标志位设置： 用三个布尔型变量 numFlag、dotFlag、eFlag 分别标记是否出现过数字、是否出现过小数点、是否出现过指数符号。

  2. 遍历字符串： 从左到右遍历字符串的每个字符。

  3. 条件判断：

    • 如果是数字，将 numFlag 置为 true。
    • 如果是小数点，需要确保小数点之前未出现过，并且指数符号未出现过，然后将 dotFlag 置为 true。
    • 如果是指数符号，需要确保指数符号之前未出现过，并且之前出现过数字，然后将 eFlag 置为 true，并重置 numFlag。
    • 如果是正负号，需要是第一个字符，或者前一个字符是指数符号，然后进行标记，并重置数字出现的标识 numFlag。
    • 如果是其他字符，返回 false。

  4. 返回结果： 最后需要确保字符串中至少出现过数字，以避免类似字符串为 “.” 或 “e” 的特殊情况。

Java 版本解题思路

  1. 标志位设置： 用三个布尔型变量 numFlag、dotFlag、eFlag 分别标记是否出现过数字、是否出现过小数点、是否出现过指数符号。

  2. 遍历字符串： 从左到右遍历字符串的每个字符。

  3. 条件判断：

    • 如果是数字，将 numFlag 置为 true。
    • 如果是小数点，需要确保小数点之前未出现过，并且指数符号未出现过，然后将 dotFlag 置为 true。
    • 如果是指数符号，需要确保指数符号之前未出现过，并且之前出现过数字，然后将 eFlag 置为 true，并重置 numFlag。
    • 如果是正负号，需要是第一个字符，或者前一个字符是指数符号，然后进行标记，并重置数字出现的标识 numFlag。
    • 如果是其他字符，返回 false。

  4. 返回结果： 最后需要确保字符串中至少出现过数字，以避免类似字符串为 “.” 或 “e” 的特殊情况。

C++ 版本解题思路

  1. 标志位设置： 用三个布尔型变量 numFlag、dotFlag、eFlag 分别标记是否出现过数字、是否出现过小数点、是否出现过指数符号。

  2. 遍历字符串： 从左到右遍历字符串的每个字符。

  3. 条件判断：

    • 如果是数字，将 numFlag 置为 true。
    • 如果是小数点，需要确保小数点之前未出现过，并且指数符号未出现过，然后将 dotFlag 置为 true。
    • 如果是指数符号，需要确保指数符号之前未出现过，并且之前出现过数字，然后将 eFlag 置为 true，并重置 numFlag。
    • 如果是正负号，需要是第一个字符，或者前一个字符是指数符号，然后进行标记，并重置数字出现的标识 numFlag。
    • 如果是其他字符，返回 false。

  4. 返回结果： 最后需要确保字符串中至少出现过数字，以避免类似字符串为 “.” 或 “e” 的特殊情况。

这些解题思路基本上都是利用标志位来记录数字、小数点和指数符号的出现情况，然后通过条件判断来验证字符串是否是一个有效的数字。希望这样的详细介绍能够帮助理解这些代码的思路。

代码

func isNumber(s string) bool {numFlag, dotFlag, eFlag := false, false, false // 用于跟踪数字、小数点和指数标志的布尔变量初始化为falsefor i := 0; i < len(s); i++ { // 循环遍历输入字符串的每个字符if '0' <= s[i] && s[i] <= '9' { // 如果当前字符是数字0-9之间的字符numFlag = true // 设置数字标志为true} else if s[i] == '.' && !dotFlag && !eFlag { // 如果当前字符是小数点，且之前未出现小数点且未出现指数符号dotFlag = true // 设置小数点标志为true} else if (s[i] == 'e' || s[i] == 'E') && !eFlag && numFlag { // 如果当前字符是指数符号 'e' 或 'E'，且之前未出现指数符号且之前出现过数字eFlag = true // 设置指数标志为truenumFlag = false // 重置数字标志以在指数符号后重新判断整数部分} else if (s[i] == '+' || s[i] == '-') && (i == 0 || s[i-1] == 'e' || s[i-1] == 'E') {// 如果当前字符是正号 '+' 或负号 '-'，且该符号在字符串开头或在指数符号 'e' 或 'E' 的后面continue // 继续循环，不执行其他操作} else {return false // 如果当前字符不满足上述任何条件，则字符串不是有效数字，返回false}}// 避免特殊情况: s == '.' 或 'e/E' 或 '+/-' 等等...// 字符串 s 必须包含数字return numFlag // 返回数字标志，如果为true，则表示字符串是有效数字，否则为false
}

Python

class Solution:def isNumber(self, s: str) -> bool:numFlag, dotFlag, eFlag = False, False, Falsefor i in range(len(s)):if '0' <= s[i] <= '9':numFlag = Trueelif s[i] == '.' and not dotFlag and not eFlag:dotFlag = Trueelif (s[i] == 'e' or s[i] == 'E') and not eFlag and numFlag:eFlag = TruenumFlag = Falseelif (s[i] == '+' or s[i] == '-') and (i == 0 or s[i-1] == 'e' or s[i-1] == 'E'):continueelse:return Falsereturn numFlag

Java

class Solution {public boolean isNumber(String s) {boolean numFlag = false, dotFlag = false, eFlag = false;for (int i = 0; i < s.length(); i++) {if (s.charAt(i) >= '0' && s.charAt(i) <= '9') {numFlag = true;} else if (s.charAt(i) == '.' && !dotFlag && !eFlag) {dotFlag = true;} else if ((s.charAt(i) == 'e' || s.charAt(i) == 'E') && !eFlag && numFlag) {eFlag = true;numFlag = false;} else if ((s.charAt(i) == '+' || s.charAt(i) == '-') && (i == 0 || s.charAt(i-1) == 'e' || s.charAt(i-1) == 'E')) {continue;} else {return false;}}return numFlag;}
}

Cpp

class Solution {
public:bool isNumber(string s) {bool numFlag = false, dotFlag = false, eFlag = false;for (int i = 0; i < s.length(); i++) {if (s[i] >= '0' && s[i] <= '9') {numFlag = true;} else if (s[i] == '.' && !dotFlag && !eFlag) {dotFlag = true;} else if ((s[i] == 'e' || s[i] == 'E') && !eFlag && numFlag) {eFlag = true;numFlag = false;} else if ((s[i] == '+' || s[i] == '-') && (i == 0 || s[i-1] == 'e' || s[i-1] == 'E')) {continue;} else {return false;}}return numFlag;}
};

每个版本的代码所需要的基础知识：

Go 版本

  1. 基础数据类型： 代码中对数字、布尔类型进行了处理，所以需要了解 Go 语言的基础数据类型，包括整数和浮点数。

  2. 字符串操作： 对字符串进行了遍历和字符比较操作，需要了解 Go 语言中字符串的基本操作。

  3. 循环和条件语句： 代码使用了 for 循环和 if 条件语句，因此需要了解 Go 中的循环和条件语句的使用。

Python 版本

  1. 基础数据类型： 代码中同样对数字、布尔类型进行了处理，因此需要了解 Python 的基础数据类型，包括整数和浮点数。

  2. 字符串操作： 对字符串进行了遍历和字符比较操作，需要了解 Python 中字符串的基本操作。

  3. 循环和条件语句： 代码使用了 for 循环和 if 条件语句，因此需要了解 Python 中的循环和条件语句的使用。

Java 版本

  1. 基础数据类型： 代码中同样对数字、布尔类型进行了处理，因此需要了解 Java 的基础数据类型，包括整数和浮点数。

  2. 字符串操作： 对字符串进行了遍历和字符比较操作，需要了解 Java 中字符串的基本操作。

  3. 循环和条件语句： 代码使用了 for 循环和 if 条件语句，因此需要了解 Java 中的循环和条件语句的使用。

C++ 版本

  1. 基础数据类型： 代码中同样对数字、布尔类型进行了处理，因此需要了解 C++ 的基础数据类型，包括整数和浮点数。

  2. 字符串操作： 对字符串进行了遍历和字符比较操作，需要了解 C++ 中字符串的基本操作。

  3. 循环和条件语句： 代码使用了 for 循环和 if 条件语句，因此需要了解 C++ 中的循环和条件语句的使用。

总体来说，这些代码都涉及到了基本的数据类型、字符串操作、循环和条件语句。如果你对这些方面有一定的了解，应该能够理解和修改这些代码。如果有具体的问题，欢迎提出。

66. Plus One

题目

Given a non-empty array of digits representing a non-negative integer, plus one to the integer.

The digits are stored such that the most significant digit is at the head of the list, and each element in the array contain a single digit.

You may assume the integer does not contain any leading zero, except the number 0 itself.

Example 1:

Input: [1,2,3]
Output: [1,2,4]
Explanation: The array represents the integer 123.

Example 2:

Input: [4,3,2,1]
Output: [4,3,2,2]
Explanation: The array represents the integer 4321.

题目大意

给定一个由整数组成的非空数组所表示的非负整数，在该数的基础上加一。最高位数字存放在数组的首位， 数组中每个元素只存储单个数字。你可以假设除了整数 0 之外，这个整数不会以零开头。

解题思路

  • 给出一个数组，代表一个十进制数，数组的 0 下标是十进制数的高位。要求计算这个十进制数加一以后的结果。
  • 简单的模拟题。从数组尾部开始往前扫，逐位进位即可。最高位如果还有进位需要在数组里面第 0 位再插入一个 1 。
    当分别介绍每个版本的解题思路时，以下是每个版本的具体思路：

Go 版本解题思路：

  1. 从数组的最后一个元素开始向前遍历，这是因为在题目中要求最高位存储在数组的首位。

  2. 对当前元素加1。

  3. 如果当前元素不等于10，说明没有进位，直接返回结果数组。

  4. 如果当前元素等于10，将当前元素设为0，表示有进位。

  5. 继续向前遍历，重复步骤2和3。

  6. 如果遍历完整个数组还有进位，说明所有元素都是9，将第一个元素设为1，然后在数组末尾添加一个0。

  7. 返回最终结果数组。

Python 版本解题思路：

  1. 从数组的最后一个元素开始向前遍历，这是因为在题目中要求最高位存储在列表的首位。

  2. 对当前元素加1，并使用carry变量来跟踪进位，初始进位设为1，因为要加1。

  3. 计算进位：用当前元素除以10，得到整数部分作为进位，用当前元素取余10，更新当前位的值。

  4. 继续向前遍历，重复步骤2和3。

  5. 如果遍历完整个列表还有进位，说明所有元素都是9，插入新的元素1在最前面。

  6. 返回最终结果列表。

Java 版本解题思路：

  1. 从数组的最后一个元素开始向前遍历，这是因为在题目中要求最高位存储在数组的首位。

  2. 对当前元素加1，并使用carry变量来跟踪进位，初始进位设为1，因为要加1。

  3. 计算进位：用当前元素除以10，得到整数部分作为进位，用当前元素取余10，更新当前位的值。

  4. 继续向前遍历，重复步骤2和3。

  5. 如果遍历完整个数组还有进位，说明所有元素都是9，创建一个新的数组，第一个元素设为进位，然后将原数组的内容复制到新数组中。

  6. 返回最终结果数组。

C++ 版本解题思路：

  1. 从数组的最后一个元素开始向前遍历，这是因为在题目中要求最高位存储在数组的首位。

  2. 对当前元素加1，并使用carry变量来跟踪进位，初始进位设为1，因为要加1。

  3. 计算进位：用当前元素除以10，得到整数部分作为进位，用当前元素取余10，更新当前位的值。

  4. 继续向前遍历，重复步骤2和3。

  5. 如果遍历完整个数组还有进位，说明所有元素都是9，创建一个新的数组，第一个元素设为进位，然后将原数组的内容复制到新数组中。

  6. 返回最终结果数组。

这些解决方案的思路都是模拟加法操作，从最低位开始逐位相加，处理进位情况，并根据最终结果是否需要额外增加新的最高位来得到最终答案。

代码

Go

func plusOne(digits []int) []int {// 从数组的最后一个元素开始向前遍历for i := len(digits) - 1; i >= 0; i-- {// 将当前元素加1digits[i]++if digits[i] != 10 {// 如果当前元素不等于10，说明没有进位// 直接返回结果数组return digits}// 如果当前元素等于10，有进位digits[i] = 0}// 如果遍历完整个数组还有进位，说明所有元素都是9// 将第一个元素设为1，然后在数组末尾添加一个0digits[0] = 1digits = append(digits, 0)// 返回最终结果数组return digits
}

Python

class Solution:def plusOne(self, digits):carry = 1  # 初始进位设为1，因为我们要加1for i in range(len(digits) - 1, -1, -1):digits[i] += carrycarry = digits[i] // 10  # 计算进位digits[i] %= 10  # 更新当前位的值if carry:digits.insert(0, 1)  # 如果仍然有进位，插入新的元素1在最前面return digits

Java

class Solution {public int[] plusOne(int[] digits) {int carry = 1;  // 初始进位设为1，因为我们要加1for (int i = digits.length - 1; i >= 0; i--) {digits[i] += carry;carry = digits[i] / 10;  // 计算进位digits[i] %= 10;  // 更新当前位的值}if (carry > 0) {int[] result = new int[digits.length + 1];result[0] = carry;  // 在数组最前面插入新的元素1System.arraycopy(digits, 0, result, 1, digits.length);  // 复制原数组的内容return result;}return digits;}
}

Cpp

class Solution {
public:vector<int> plusOne(vector<int>& digits) {int carry = 1;  // 初始进位设为1，因为我们要加1for (int i = digits.size() - 1; i >= 0; i--) {digits[i] += carry;carry = digits[i] / 10;  // 计算进位digits[i] %= 10;  // 更新当前位的值}if (carry > 0) {digits.insert(digits.begin(), carry);  // 在向量最前面插入新的元素1}return digits;}
};

当分别介绍每个版本的解决方案时，需要了解以下基础知识：

Go 版本：

  1. 数组和切片（Array and Slice）：Go中的数组和切片是基本数据结构，理解它们的索引、遍历、和元素访问是必须的。

  2. 循环（Loop）：Go版本使用for循环来遍历数组，需要了解for循环的基本语法。

  3. 切片操作（Slice Manipulation）：Go中的切片操作允许您在数组中进行增加和减少元素，需要了解如何在切片中添加元素。

Python 版本：

  1. 列表（List）：Python中的列表类似于数组，是一种有序的数据结构。需要了解如何访问列表元素、遍历列表以及列表的基本操作。

  2. 循环（Loop）：Python使用for循环来遍历列表，需要了解for循环的基本语法。

  3. 整数除法和取余运算（Integer Division and Modulus）：在Python中，整数相除使用//运算符，取余使用%运算符。

Java 版本：

  1. 数组（Array）：Java中的数组是一种固定大小的数据结构，需要了解如何声明、初始化和访问数组元素。

  2. 循环（Loop）：Java使用for循环来遍历数组，需要了解for循环的语法。

  3. 整数除法和取余运算（Integer Division and Modulus）：了解如何使用整数除法/和取余%运算符。

  4. 条件语句（Conditional Statements）：在Java中，if语句用于条件判断，需要了解如何编写条件语句。

  5. 数组复制（Array Copy）：Java中可以使用System.arraycopy来复制数组的内容。

C++ 版本：

  1. 数组（Array）：C++中的数组是一种固定大小的数据结构，需要了解如何声明、初始化和访问数组元素。

  2. 循环（Loop）：C++使用for循环来遍历数组，需要了解for循环的语法。

  3. 整数除法和取余运算（Integer Division and Modulus）：了解如何使用整数除法/和取余%运算符。

  4. 条件语句（Conditional Statements）：在C++中，if语句用于条件判断，需要了解如何编写条件语句。

  5. 向量（Vector）：C++中的vector是一种动态数组，可以使用push_back方法向向量添加元素。在这个解决方案中，使用vector来在数组前插入新元素。

67. Add Binary

题目

Given two binary strings, return their sum (also a binary string).

The input strings are both non-empty and contains only characters 1 or 0.

Example 1:

Input: a = "11", b = "1"
Output: "100"

Example 2:

Input: a = "1010", b = "1011"
Output: "10101"

题目大意

给你两个二进制字符串，返回它们的和（用二进制表示）。输入为 非空 字符串且只包含数字 1 和 0。

解题思路

  • 要求输出 2 个二进制数的和，结果也用二进制表示。
  • 简单题。按照二进制的加法规则做加法即可。
    继续解释每个版本的代码的思路和实现：

Go 版本解题思路：

  1. 代码首先检查输入的两个二进制字符串，如果其中一个比另一个长，就进行交换，确保 a 永远比 b 长。
  2. 创建一个结果切片 res 用于存储最终结果，长度初始化为 len(a) + 1，以容纳可能的最高位进位。
  3. 使用三个指针 i、j 和 k，i 和 j 分别从 a 和 b 的最低位开始向左遍历，k 从 res 的最高位开始向左遍历。
  4. 在循环中，对应位的值（0 或 1）从 a 和 b 中提取并与进位 c 相加，然后更新 res[k] 为该位的结果，并计算新的进位值。
  5. 遍历结束后，如果仍有进位，将进位的值 c 放入 res 的最高位。
  6. 最后，使用 strings.Join 将结果切片中的字符串元素连接在一起，并返回最终的二进制字符串。

Python 版本解题思路：

  1. 代码首先检查输入的两个二进制字符串，如果其中一个比另一个长，就进行交换，确保 a 永远比 b 长。
  2. 创建一个结果字符列表 res 用于存储最终结果。
  3. 使用三个指针 i、j 和 k，i 和 j 分别从 a 和 b 的最低位开始向左遍历，k 从 res 的最高位开始向左遍历。
  4. 在循环中，对应位的值（‘0’ 或 ‘1’）从 a 和 b 中提取并与进位 c 相加，然后将当前位的结果添加到 res 中，并计算新的进位值。
  5. 遍历结束后，如果仍有进位，将进位的值 c 作为最高位添加到 res 中。
  6. 最后，将结果字符列表中的字符连接在一起，返回最终的二进制字符串。

Java 版本解题思路：

  1. 如果两个输入字符串的长度不同，代码会交换它们，以确保 a 始终比 b 长。
  2. 创建一个字符数组用于存储结果，长度为 a.length() + 1（以容纳可能的最高位进位）。
  3. 从最低位（字符串的末尾）开始逐位相加。
  4. 对于每一对相应的位，考虑进位，然后计算当前位的值并更新进位。
  5. 将当前位的值（‘0’ 或 ‘1’）存储在结果字符数组中。
  6. 如果循环结束后仍然有进位，将进位（‘0’ 或 ‘1’）放在结果字符数组的最高位。
  7. 根据进位情况返回最终的二进制字符串，去掉可能的前导零。

C++ 版本解题思路：

  1. 如果两个输入字符串的长度不同，代码会交换它们，以确保 a 始终比 b 长。
  2. 创建一个字符串（std::string）用于存储结果。
  3. 从最低位（字符串的末尾）开始逐位相加。
  4. 对于每一对相应的位，考虑进位，然后计算当前位的值并更新进位。
  5. 将当前位的值（‘0’ 或 ‘1’）添加到结果字符串中。
  6. 如果循环结束后仍然有进位，将进位（‘0’ 或 ‘1’）添加到结果字符串的最高位。
  7. 最后，返回最终的二进制字符串。

在所有版本中，主要思路都是处理进位，逐位相加并生成结果，最后处理可能的前导零。这些实现根据各自编程语言的特性和库函数来操作字符串、数组或切片。

代码


package leetcodeimport ("strconv""strings"
)func addBinary(a string, b string) string {if len(b) > len(a) {a, b = b, a}res := make([]string, len(a)+1)i, j, k, c := len(a)-1, len(b)-1, len(a), 0for i >= 0 && j >= 0 {ai, _ := strconv.Atoi(string(a[i]))bj, _ := strconv.Atoi(string(b[j]))res[k] = strconv.Itoa((ai + bj + c) % 2)c = (ai + bj + c) / 2i--j--k--}for i >= 0 {ai, _ := strconv.Atoi(string(a[i]))res[k] = strconv.Itoa((ai + c) % 2)c = (ai + c) / 2i--k--}if c > 0 {res[k] = strconv.Itoa(c)}return strings.Join(res, "")
}

代码

Go

func addBinary(a string, b string) string {m, n := len(a), len(b)max := m// 确保a和b的长度一致，如果不一致，将短的字符串前面补0，使它们长度相等if m > n {b = strings.Repeat("0", m-n) + b} else if n > m {max = na = strings.Repeat("0", n-m) + a}res := make([]byte, max)var carry byte// 从最高位开始逐位相加for i := max - 1; i >= 0; i-- {tmp := a[i] - '0' + b[i] - '0' + carryres[i] = tmp % 2carry = tmp / 2}// 如果最高位有进位，添加1到结果的最前面if carry > 0 {res = append([]byte{1}, res...)}s := ""// 将结果转换为字符串for i := 0; i < len(res); i++ {s += strconv.Itoa(int(res[i]))}return s
}

Python

class Solution:def addBinary(self, a: str, b: str) -> str:# 确保b的长度不大于a，如果b更长，交换它们if len(b) > len(a):a, b = b, ares = [''] * (len(a) + 1)i, j, k, c = len(a) - 1, len(b) - 1, len(a), 0while i >= 0 and j >= 0:ai = int(a[i])bj = int(b[j])res[k] = str((ai + bj + c) % 2)c = (ai + bj + c) // 2i -= 1j -= 1k -= 1while i >= 0:ai = int(a[i])res[k] = str((ai + c) % 2)c = (ai + c) // 2i -= 1k -= 1if c > 0:res[k] = str(c)return ''.join(res)

Java

class Solution {public static String addBinary(String a, String b) {// 如果a的长度小于b的长度，交换a和bif (a.length() < b.length()) {return addBinary(b, a);}// 创建一个字符数组，用于存储相加的结果，长度比a的长度多1char[] sum = new char[a.length() + 1];int indexA = a.length() - 1; // a的索引int diffLen = a.length() - b.length(); // a和b的长度差char carry = '0'; // 进位初始化为0// 从最低位开始逐位相加while (indexA > -1) {char bitB = indexA - diffLen > -1 ? b.charAt(indexA - diffLen) : '0'; // 获取b的对应位或补0if (a.charAt(indexA) == bitB) {sum[indexA + 1] = carry;carry = bitB;} else {sum[indexA + 1] = carry == '0' ? '1' : '0';}indexA--;}sum[0] = carry; // 设置最高位// 根据进位返回最终的二进制字符串，去掉可能的前导零return carry == '1' ? new String(sum, 0, a.length() + 1) : new String(sum, 1, a.length());}
}

Cpp

class Solution {
public:string addBinary(string a, string b) {int m = a.length();int n = b.length();int maxLen = max(m, n);// 确保a和b的长度一致，如果不一致，将短的字符串前面补0，使它们长度相等if (m > n) {b = string(m - n, '0') + b;
…        return res;}
};

当处理LeetCode问题时，不同的编程语言可能需要不同的基础知识。以下是每个版本的实现需要的基础知识和关键概念的详细介绍：

Go 版本：

  • 字符串操作：Go中有许多内置函数和方法用于字符串操作，例如strings.Repeat和strings.Join。在这个实现中，它们用于处理二进制字符串的填充和拼接。
  • 切片（Slices）：Go中的切片是动态数组，它们用于存储结果。在循环中，切片的长度可能会发生变化，这需要了解如何使用切片来动态管理数据。

Python 版本：

  • 字符串操作：Python提供了丰富的字符串操作方法。在这个实现中，您会看到str类型的字符串，以及字符串的切片和拼接操作。
  • 列表（Lists）：Python中的列表类似于数组，它们用于存储结果。了解如何创建、修改和迭代列表是很重要的。
  • 整数和字符之间的转换：在实现中，您需要将字符(‘0’ 和 ‘1’)转换为整数，以便进行加法操作。Python提供了int和str之间的转换方法。

Java 版本：

  • 字符串操作：Java中的字符串是不可变的，但在这个实现中，您需要了解如何创建和操作字符数组以构建结果字符串。
  • 字符和整数之间的转换：在实现中，需要将字符（‘0’ 和 ‘1’）转换为整数。Java提供了Character.getNumericValue方法来执行这种转换。
  • 数组：Java中的数组用于存储结果。了解如何创建、修改和访问数组元素非常重要。

C++ 版本：

  • 字符串操作：C++中的字符串可以使用std::string来表示，而std::to_string函数用于将整数转换为字符串。这在处理二进制字符串的填充和结果字符串的构建中很有用。
  • 字符和整数之间的转换：需要将字符（‘0’ 和 ‘1’）转换为整数。C++提供了std::stoi函数来执行这种转换。
  • 数组（Vectors）：C++中的std::vector类似于动态数组，用于存储结果。了解如何创建、修改和访问std::vector元素是很重要的。

在每个版本中，还需要理解循环结构和逻辑控制，以便正确地执行二进制加法。此外，要处理进位和结果的拼接，需要了解位运算和字符串操作的基础知识。

不管使用哪种编程语言，理解二进制加法的规则和位运算是解决这个问题的关键。在实际编码中，根据编程语言的特性，选择合适的数据结构和字符串操作方法来实现算法是很重要的。

68.Text-Justification

题目

  1. Text-Justification

Given an array of strings words and a width maxWidth, format the text such that each line has exactly maxWidth characters and is fully (left and right) justified.

You should pack your words in a greedy approach; that is, pack as many words as you can in each line. Pad extra spaces ’ ’ when necessary so that each line has exactly maxWidth characters.

Extra spaces between words should be distributed as evenly as possible. If the number of spaces on a line does not divide evenly between words, the empty slots on the left will be assigned more spaces than the slots on the right.

For the last line of text, it should be left-justified, and no extra space is inserted between words.

Note:

A word is defined as a character sequence consisting of non-space characters only.
Each word’s length is guaranteed to be greater than 0 and not exceed maxWidth.
The input array words contains at least one word.

Example 1:

Input: words = [“This”, “is”, “an”, “example”, “of”, “text”, “justification.”], maxWidth = 16
Output:
[
“This is an”,
“example of text”,
"justification. "
]
Example 2:

Input: words = [“What”,“must”,“be”,“acknowledgment”,“shall”,“be”], maxWidth = 16
Output:
[
“What must be”,
"acknowledgment ",
"shall be "
]
Explanation: Note that the last line is "shall be " instead of “shall be”, because the last line must be left-justified instead of fully-justified.
Note that the second line is also left-justified because it contains only one word.
Example 3:

Input: words = [“Science”,“is”,“what”,“we”,“understand”,“well”,“enough”,“to”,“explain”,“to”,“a”,“computer.”,“Art”,“is”,“everything”,“else”,“we”,“do”], maxWidth = 20
Output:
[
“Science is what we”,
“understand well”,
“enough to explain to”,
“a computer. Art is”,
“everything else we”,
"do "
]

Constraints:

1 <= words.length <= 300
1 <= words[i].length <= 20
words[i] consists of only English letters and symbols.
1 <= maxWidth <= 100
words[i].length <= maxWidth

题目大意

给定一个单词数组 words 和一个长度 maxWidth ，重新排版单词，使其成为每行恰好有 maxWidth 个字符，且左右两端对齐的文本。

你应该使用 “贪心算法” 来放置给定的单词；也就是说，尽可能多地往每行中放置单词。必要时可用空格 ’ ’ 填充，使得每行恰好有 maxWidth 个字符。

要求尽可能均匀分配单词间的空格数量。如果某一行单词间的空格不能均匀分配，则左侧放置的空格数要多于右侧的空格数。

文本的最后一行应为左对齐，且单词之间不插入额外的空格。

解题思路

以下是每个版本的解题思路的分别介绍：

Go 版本
Go 版本使用贪心算法来解决文本两端对齐问题，主要思路如下：

  1. 初始化右边界 right 和单词总数 n。
  2. 通过循环遍历每个单词，找到适合当前行的单词，使得当前行的总长度不超过 maxWidth。
  3. 如果已经处理完了最后一个单词，特殊处理最后一行，左对齐并且不插入额外空格。
  4. 如果当前行不只包含一个单词，计算单词间需要插入的空格数，将空格尽可能均匀分配，注意处理额外的空格。
  5. 构建当前行的字符串，将其加入结果列表。
  6. 重复步骤2-5直到处理完所有单词。

这个思路实现了文本两端对齐的要求，使用贪心算法来尽可能均匀分配空格，以满足每行有 maxWidth 字符的条件。

Python 版本
Python 版本使用贪心算法解决文本两端对齐问题，主要思路如下：

  1. 初始化一个空列表 result，用于存储最终结果。
  2. 初始化一个空列表 cur_line，用于存储当前行的单词。
  3. 初始化 cur_width 为0，表示当前行的宽度。
  4. 遍历每个单词，将单词逐个加入 cur_line，同时计算当前行的宽度。
  5. 如果当前行已满或者不能再加入单词，进行对齐处理，并将当前行加入 result。
  6. 如果当前行为空，处理最后一行的左对齐。
  7. 返回 result 列表，包含对齐好的文本。

这个思路实现了文本两端对齐的要求，使用贪心算法来尽可能均匀分配空格，以满足每行有 maxWidth 字符的条件。

Java 版本
Java 版本采用贪心算法解决文本两端对齐问题，主要思路如下：

  1. 初始化一个空列表 res，用于存储最终结果。
  2. 通过循环遍历每个单词，以及跟踪左边界和当前行的长度。
  3. 尽可能多地加入单词到当前行，使得长度不超过 maxWidth。
  4. 如果当前行只有一个单词，左对齐处理。
  5. 如果是最后一行，左对齐且单词之间只加一个空格。
  6. 否则，尽可能均匀分配单词之间的空格，考虑额外的空格。
  7. 构建当前行的字符串，将其加入 res 列表。
  8. 重复步骤2-7直到处理完所有单词。

这个思路实现了文本两端对齐的要求，使用贪心算法来尽可能均匀分配空格，以满足每行有 maxWidth 字符的条件。

C++ 版本
C++ 版本采用贪心算法解决文本两端对齐问题，主要思路如下：

  1. 初始化一些变量，包括计数器、当前行的单词列表、最终结果的列表等。
  2. 通过循环遍历每个单词，找到适合当前行的单词，使得当前行的总长度不超过 maxWidth。
  3. 特殊处理只包含一个单词的情况，左对齐并在单词后面填充额外空格。
  4. 特殊处理最后一行，左对齐并在单词之间只加一个空格。
  5. 否则，尽可能均匀分配单词之间的空格，考虑额外的空格。
  6. 构建当前行的字符串，将其加入结果列表。
  7. 重复步骤2-6直到处理完所有单词。

这个思路实现了文本两端对齐的要求，使用贪心算法来尽可能均匀分配空格，以满足每行有 maxWidth 字符的条件。

代码

Go

// blank 返回长度为 n 的由空格组成的字符串
func blank(n int) string {return strings.Repeat(" ", n)
}// fullJustify 实现文本两端对齐
func fullJustify(words []string, maxWidth int) (ans []string) {right, n := 0, len(words)  // 初始化右边界和单词总数for {left := right // 当前行的第一个单词在 words 的位置sumLen := 0   // 统计这一行单词长度之和// 循环获取适合当前行的单词for right < n && sumLen+len(words[right])+right-left <= maxWidth {sumLen += len(words[right])right++}// 边界条件，如果已经处理完最后一个单词if right == n {var s stringfor i := left; i < right; i++ {s += words[i] + " "}// 去掉最后一个单词的多余空格ans = append(ans, s[:len(s)-1]+blank(maxWidth-len(s)+1))return ans}// 当前行不只一个单词numWords := right - leftnumSpaces := maxWidth - sumLenavgSpaces := numSpaces / (numWords - 1)  // 平均空格数extraSpaces := numSpaces % (numWords - 1)  // 额外空格数s1 := strings.Join(words[left:left+extraSpaces+1], blank(avgSpaces+1)) // 拼接额外加一个空格的单词s2 := strings.Join(words[left+extraSpaces+1:right], blank(avgSpaces))  // 拼接其余单词ans = append(ans, s1+blank(avgSpaces)+s2)  // 将构建好的当前行加入结果列表}
}

Python

from typing import Listclass Solution:def fullJustify(self, words: List[str], maxWidth: int) -> List[str]:result = []  # 存储最终结果的列表cur_line = []  # 当前行的单词列表cur_width = 0  # 当前行的宽度for word in words:  # 遍历每个单词if cur_width + len(cur_line) + len(word) <= maxWidth:  # 如果当前行可以容纳该单词cur_line.append(word)  # 将单词加入当前行cur_width += len(word)  # 更新当前行的宽度else:  # 当前行不能容纳该单词result.append(self.align(cur_line, cur_width, maxWidth))  # 对当前行进行对齐处理并加入结果列表cur_line = [word]  # 初始化下一行cur_width = len(word)  # 更新当前行宽度if cur_line:  # 处理最后一行result.append(' '.join(cur_line).ljust(maxWidth))  # 最后一行左对齐处理return result  # 返回最终结果列表def align(self, line, cur_width, maxWidth):  # 对齐函数if len(line) == 1:  # 如果当前行只有一个单词return line[0].ljust(maxWidth)  # 左对齐处理total_space = maxWidth - cur_width  # 总空格数space_slot = len(line) - 1  # 空格插槽数量if space_slot == 0:  # 如果只有一个单词return line[0] + ' ' * total_space  # 在单词后面填充剩余空格space_between_words, extra_space = divmod(total_space, space_slot)  # 计算平均每个空格数和多余的空格数spaces = ' ' * space_between_words  # 构建平均空格for i in range(extra_space):  # 分配多余的空格line[i] += ' 'return spaces.join(line)  # 返回对齐后的字符串

Java

class Solution {public List<String> fullJustify(String[] words, int maxWidth) {List<String> res = new ArrayList<>(); // 存储最终结果的列表int n = words.length; // 单词总数int i = 0; // 初始化索引while (i < n) { // 遍历每个单词int len = 0; // 当前行已选单词的长度int wordsNum = 0; // 当前行已选单词的数量StringBuilder sb = new StringBuilder(); // 用于构建当前行的字符串while (i < n && len + words[i].length() + wordsNum <= maxWidth) {// 选取单词len += words[i].length();wordsNum++;i++;}if (wordsNum == 1) { // 如果当前行只有一个单词，左对齐sb.append(words[i - wordsNum]);for (int j = 0; j < maxWidth - len; j++) {sb.append(" ");}} else if (i == n) { // 如果是最后一行，左对齐且单词之间只加一个空格for (int j = i - wordsNum; j < i; j++) {sb.append(words[j]);if (j < i - 1) {sb.append(" ");}}for (int j = 0; j < maxWidth - len - (wordsNum - 1); j++) {sb.append(" ");}} else { // 否则，尽可能均匀分配单词间的空格数量int spaces = maxWidth - len;int slots = wordsNum - 1;int spaceWidth = spaces / slots;int remain = spaces % slots;for (int j = i - wordsNum; j < i; j++) {sb.append(words[j]);if (j == i - 1) {break;}for (int k = 0; k < spaceWidth; k++) {sb.append(" ");}if (remain > 0) {sb.append(" ");remain--;}}}res.add(sb.toString()); // 将构建好的当前行加入结果列表}return res; // 返回最终结果列表}
}

Cpp

class Solution {
public:vector<string> fullJustify(vector<string>& words, int maxWidth) {int n = words.size(), sum = 0, index = 0, countSize = 0;  // 初始化变量string str = "";  // 用于构建当前行的字符串vector<string> vec1;  // 存储当前行的单词vector<string> vec2;  // 存储最终结果for (int i = 0; i < n && index < n; ++i)  // 遍历每个单词{index = i;  // 初始化索引while (index < n)  // 在当前行内遍历单词{if (sum == 0)  // 如果当前行还没有单词{str += words[index];  // 将单词添加到当前行sum++;countSize += words[index++].size();  // 更新当前行的字符数vec1.push_back(words[i]);  // 将单词添加到当前行的单词列表continue;}else if (sum > 0)  // 如果当前行已有单词{int tmp = words[index].size() + vec1.size() - 1;  // 计算加入新单词后的字符数if (tmp + countSize < maxWidth)  // 如果加入新单词后不超过最大宽度{countSize += words[index].size();str += " " + words[index];  // 在当前行末尾加入单词vec1.push_back(words[index++]);  // 将单词添加到当前行的单词列表sum++;continue;}else  // 如果加入新单词后超过了最大宽度{int sub = maxWidth - countSize;  // 计算需要填充的空格数if (vec1.size() - 1 > 0)  // 如果当前行单词数大于1{int div = sub / (vec1.size() - 1);  // 平均每个空隙填充的空格数int rem = sub % (vec1.size() - 1);  // 剩余的空格数for (int j = vec1.size() - sum; j < vec1.size() - 1; j++)  // 在单词之间填充空格{int cir = 0;while (cir++ < div)vec1[j] += " ";}for (int k = vec1.size() - sum; k < vec1.size() - sum + rem; k++)  // 在单词之间均匀填充剩余空格{vec1[k] += " ";}str = "";for (int v = vec1.size() - sum; v < vec1.size(); v++)  // 构建当前行的字符串{str += vec1[v];}}else  // 如果只有一个单词{if (countSize > 0){for (int i = 0; i < maxWidth - countSize; ++i)  // 在单词之后填充剩余的空格{str += " ";}}}vec2.push_back(str);  // 将构建好的当前行加入结果列表str = "";i += sum - 1;  // 跳过已处理的单词sum = 0, countSize = 0;  // 重置当前行的变量vec1.clear();  // 清空当前行的单词列表break;  // 跳出循环}}}}if (countSize > 0)  // 处理最后一行{for (int i = 0; i < maxWidth - countSize  - (sum - 1); ++i)  // 在最后一行填充剩余的空格{str += " ";}vec2.push_back(str);  // 将最后一行加入结果列表}return vec2;  // 返回最终结果列表}
};

当您用中文进行编程时，了解每个版本的代码所需的基础知识可以帮助您更好地理解和使用这些代码。以下是每个版本的基础知识要点：

Go 版本

  1. Go 语言: 您需要了解 Go 编程语言的基础知识，包括变量、函数、数组、切片、字符串处理等。
  2. 字符串处理: 了解如何处理字符串，如字符串连接、重复、判断长度等。
  3. 循环与条件语句: 理解 Go 中的循环和条件语句，以便实现文本两端对齐。
  4. 切片: 了解 Go 中的切片数据结构，用于处理单词列表的添加和删除。
  5. 函数和函数调用: 了解如何定义和调用函数，特别是fullJustify函数。
  6. Greedy 贪心算法: 理解贪心算法的概念，它是解决文本两端对齐问题的核心。

Python 版本

  1. Python 语言: 熟悉 Python 编程语言的基础知识，包括变量、列表、字符串、函数等。
  2. 列表(List): 了解如何使用 Python 的列表来存储和操作单词。
  3. 字符串处理: 了解字符串连接、长度计算、左对齐等字符串处理方法。
  4. 循环与条件语句: 熟悉 Python 的循环和条件语句，用于遍历单词和判断对齐方式。
  5. Greedy 贪心算法: 了解贪心算法的应用，以便实现文本两端对齐。
  6. 类(Class): 了解 Python 类的概念，其中定义了 Solution 类，包含了文本对齐的方法。

Java 版本

  1. Java 语言: 了解 Java 编程语言的基础知识，包括类、数组、字符串处理、循环等。
  2. 数组(Array): 熟悉 Java 中的数组数据结构，用于存储单词。
  3. 字符串处理: 了解字符串的基本操作，如连接、长度计算、填充等。
  4. 循环与条件语句: 理解 Java 中的循环和条件语句，用于遍历单词和判断对齐方式。
  5. Greedy 贪心算法: 了解贪心算法的应用，以便实现文本两端对齐。
  6. ArrayList: 了解 Java 的 ArrayList 类，它用于存储每一行的单词。

C++ 版本

  1. C++ 语言: 熟悉 C++ 编程语言的基础知识，包括类、向量、字符串处理、循环等。
  2. 向量(Vector): 了解 C++ 中的向量数据结构，用于存储单词和文本行。
  3. 字符串处理: 了解字符串连接、长度计算、填充等字符串处理方法。
  4. 循环与条件语句: 了解 C++ 中的循环和条件语句，用于遍历单词和判断对齐方式。
  5. Greedy 贪心算法: 了解贪心算法的应用，以便实现文本两端对齐。
  6. C++ 标准库: 熟悉 C++ 标准库中的数据结构和函数，如字符串处理函数。

无论您选择哪个版本，理解编程语言的基础知识、数据结构和算法概念都是非常重要的，以便有效地理解和修改代码以满足自己的需求。这些基础知识将帮助您理解文本两端对齐问题的解决方案。

69. Sqrt(x)

题目

Implementint sqrt(int x).

Compute and return the square root ofx, wherexis guaranteed to be a non-negative integer.

Since the return typeis an integer, the decimal digits are truncated and only the integer part of the resultis returned.

Example 1:

Input: 4
Output: 2

Example 2:

Input: 8
Output: 2
Explanation: The square root of 8 is 2.82842..., and since the decimal part is truncated, 2 is returned.

题目大意

实现int sqrt(int x)函数。计算并返回x的平方根，其中x 是非负整数。由于返回类型是整数，结果只保留整数的部分，小数部分将被舍去。

解题思路

  • 题目要求求出根号 x

  • 根据题意，根号 x 的取值范围一定在 [0,x] 之间，这个区间内的值是递增有序的，有边界的，可以用下标访问的，满足这三点正好也就满足了二分搜索的 3 大条件。所以解题思路一，二分搜索。

  • 解题思路二，牛顿迭代法。求根号 x，即求满足 x^2 - n = 0 方程的所有解。

代码

Go

// 定义一个函数 mySqrt，用于计算整数 x 的平方根
func mySqrt(x int) int {// 如果 x 为 0，直接返回 0if x == 0 {return 0}// 如果 x 小于 4，直接返回 1，因为 1 的平方是 1，2 的平方是 4，3 的平方是 9if x < 4 {return 1}// 调用 binarySearch2 函数进行二分查找，寻找 x 的平方根res := binarySearch2(2, x/2, x)// 如果找到的平方根的平方大于 x，则返回平方根减 1if res*res > x {return res - 1}// 否则直接返回找到的平方根return res
}// 定义一个二分查找函数 binarySearch2，用于在区间 [l, r] 中寻找 target 的平方根
func binarySearch2(l, r, target int) int {// 使用循环进行二分查找for l < r {// 计算中间值 mid，避免溢出使用位运算mid := l + ((r - l) >> 1)// 计算中间值的平方tmp := mid * mid// 如果中间值的平方等于目标值，则直接返回中间值if tmp == target {return mid} else if tmp < target {// 如果中间值的平方小于目标值，则将搜索范围缩小到[mid+1, r]l = mid + 1} else {// 如果中间值的平方大于目标值，则将搜索范围缩小到[l, mid-1]r = mid - 1}}// 如果循环结束时 l >= r，返回 l 即可return l
}

Python

class Solution:def mySqrt(self, x: int) -> int:if x == 0:return 0if x < 4:return 1res = self.binarySearch(2, x // 2, x)if res * res > x:return res - 1return resdef binarySearch(self, l, r, target):while l < r:mid = l + ((r - l) >> 1)tmp = mid * midif tmp == target:return midelif tmp < target:l = mid + 1else:r = mid - 1return l

Java

class Solution {public int mySqrt(int x) {if (x == 0) {return 0;}// 将 C 初始化为 x，x0 初始化为 xdouble C = x, x0 = x;// 使用牛顿迭代法逼近平方根while (true) {// 计算下一个迭代值 xidouble xi = 0.5 * (x0 + C / x0);// 如果当前迭代值与上一次迭代值之差小于 1e-7，则认为已经逼近到足够精度，跳出循环if (Math.abs(x0 - xi) < 1e-7) {break;}// 更新迭代值 x0x0 = xi;}// 将最终的浮点数转换为整数并返回return (int) x0;}
}

Cpp

class Solution {
public:int mySqrt(int x) {if (x == 0) {return 0;}double C = x, x0 = x;while (true) {double xi = 0.5 * (x0 + C / x0);if (fabs(x0 - xi) < 1e-7) {break;}x0 = xi;}return int(x0);}
};

70. Climbing Stairs

题目

You are climbing a stair case. It takes n steps to reach to the top.

Each time you can either climb 1 or 2 steps. In how many distinct ways can you climb to the top?

Note: Given n will be a positive integer.

Example 1:

Input: 2
Output: 2
Explanation: There are two ways to climb to the top.
1. 1 step + 1 step
2. 2 steps

Example 2:

Input: 3
Output: 3
Explanation: There are three ways to climb to the top.
1. 1 step + 1 step + 1 step
2. 1 step + 2 steps
3. 2 steps + 1 step

题目大意

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？注意：给定 n 是一个正整数

解题思路

  • 简单的 DP，经典的爬楼梯问题。一个楼梯可以由 n-1 和 n-2 的楼梯爬上来。
  • 这一题求解的值就是斐波那契数列。
    当解决LeetCode上的爬楼梯问题时，每个版本的解题思路都基本相同，使用了动态规划的思想，将问题拆分为子问题并存储中间结果以提高效率。以下是每个版本的解题思路的详细介绍：

Go 版本解题思路

  1. 创建一个长度为 n+1 的整数切片 dp，用于存储每个台阶对应的爬楼方法数。

  2. 初始化 dp 切片的前两个元素为 1，因为爬到第一个台阶和第二个台阶的方法数都是 1。

  3. 从第三个台阶开始，使用循环依次计算每个台阶的爬楼方法数。每个台阶的爬楼方法数等于前两个台阶的爬楼方法数之和。

  4. 最后返回爬到第 n 个台阶的方法数，即 dp 切片的最后一个元素。

这个思路将问题分解成了子问题，避免了重复计算，提高了效率。

Python 版本解题思路

  1. 创建一个长度为 n+1 的列表 dp，用于存储每个台阶对应的爬楼方法数。

  2. 初始化 dp 列表的前两个元素为 1，因为爬到第一个台阶和第二个台阶的方法数都是 1。

  3. 从第三个台阶开始，使用循环依次计算每个台阶的爬楼方法数。每个台阶的爬楼方法数等于前两个台阶的爬楼方法数之和。

  4. 最后返回爬到第 n 个台阶的方法数，即 dp 列表的最后一个元素。

这个思路与Go版本类似，使用了相同的动态规划方法来解决问题。

Java 版本解题思路

  1. 创建一个长度为 n+1 的整数数组 dp，用于存储每个台阶对应的爬楼方法数。

  2. 初始化 dp 数组的前两个元素为 1，因为爬到第一个台阶和第二个台阶的方法数都是 1。

  3. 从第三个台阶开始，使用循环依次计算每个台阶的爬楼方法数。每个台阶的爬楼方法数等于前两个台阶的爬楼方法数之和。

  4. 最后返回爬到第 n 个台阶的方法数，即 dp 数组的最后一个元素。

这个思路与Go和Python版本相似，但使用了Java特定的语法和数组结构。

C++ 版本解题思路

  1. 创建一个长度为 n+1 的整数向量 dp，用于存储每个台阶对应的爬楼方法数。

  2. 初始化 dp 向量的前两个元素为 1，因为爬到第一个台阶和第二个台阶的方法数都是 1。

  3. 从第三个台阶开始，使用循环依次计算每个台阶的爬楼方法数。每个台阶的爬楼方法数等于前两个台阶的爬楼方法数之和。

  4. 最后返回爬到第 n 个台阶的方法数，即 dp 向量的最后一个元素。

这个思路与Go、Python和Java版本类似，但使用了C++特定的语法和向量数据结构。

代码

Go

func climbStairs(n int) int {// 创建一个长度为 n+1 的整数切片 dp，用于存储每个台阶对应的爬楼方法数dp := make([]int, n+1)// 初始化 dp 切片的前两个元素为 1，因为爬到第一个台阶和第二个台阶的方法数都是 1dp[0], dp[1] = 1, 1// 从第三个台阶开始，依次计算每个台阶的爬楼方法数for i := 2; i <= n; i++ {// 当前台阶的爬楼方法数等于前两个台阶的爬楼方法数之和dp[i] = dp[i-1] + dp[i-2]}// 返回爬到第 n 个台阶的方法数，即 dp 切片的最后一个元素return dp[n]
}

Python

class Solution:def climbStairs(self, n: int) -> int:# 创建一个长度为 n+1 的列表 dp，用于存储每个台阶对应的爬楼方法数dp = [0] * (n + 1)# 初始化 dp 列表的前两个元素为 1，因为爬到第一个台阶和第二个台阶的方法数都是 1dp[0], dp[1] = 1, 1# 从第三个台阶开始，依次计算每个台阶的爬楼方法数for i in range(2, n + 1):# 当前台阶的爬楼方法数等于前两个台阶的爬楼方法数之和dp[i] = dp[i - 1] + dp[i - 2]# 返回爬到第 n 个台阶的方法数，即 dp 列表的最后一个元素return dp[n]

Java

class Solution {public int climbStairs(int n) {// 创建一个长度为 n+1 的数组 dp，用于存储每个台阶对应的爬楼方法数int[] dp = new int[n + 1];// 初始化 dp 数组的前两个元素为 1，因为爬到第一个台阶和第二个台阶的方法数都是 1dp[0] = 1;dp[1] = 1;// 从第三个台阶开始，依次计算每个台阶的爬楼方法数for (int i = 2; i <= n; i++) {// 当前台阶的爬楼方法数等于前两个台阶的爬楼方法数之和dp[i] = dp[i - 1] + dp[i - 2];}// 返回爬到第 n 个台阶的方法数，即 dp 数组的最后一个元素return dp[n];}
}

Cpp

class Solution {
public:int climbStairs(int n) {// 创建一个长度为 n+1 的数组 dp，用于存储每个台阶对应的爬楼方法数vector<int> dp(n + 1, 0);// 初始化 dp 数组的前两个元素为 1，因为爬到第一个台阶和第二个台阶的方法数都是 1dp[0] = 1;dp[1] = 1;// 从第三个台阶开始，依次计算每个台阶的爬楼方法数for (int i = 2; i <= n; i++) {// 当前台阶的爬楼方法数等于前两个台阶的爬楼方法数之和dp[i] = dp[i - 1] + dp[i - 2];}// 返回爬到第 n 个台阶的方法数，即 dp 数组的最后一个元素return dp[n];}
};

当使用不同的编程语言来解决LeetCode上的爬楼梯问题时，需要了解一些基础知识，包括语言特定的语法和数据结构。以下是每个版本的所需基础知识的详细介绍：

Go 版本

  1. 包导入和函数声明： 在Go中，您需要了解如何导入包和声明函数。代码中使用的func climbStairs(n int) int是一个函数声明的示例，其中int是参数类型，后面的int是返回值类型。

  2. 切片（Slices）： Go使用切片来动态分配数组，您需要了解如何创建和初始化切片，以及如何访问和修改切片中的元素。在这个示例中，切片用于存储爬楼方法数。

  3. 循环： 您需要了解如何使用for循环来迭代数组或切片。在这里，循环用于计算每个楼梯的爬楼方法数。

Python 版本

  1. 类和方法： Python中的解决方法可以定义为类的方法。您需要了解如何声明类和方法。在这个示例中，climbStairs是一个类方法，接受参数n。

  2. 列表（Lists）： Python中的列表用于存储数据。您需要了解如何创建和初始化列表，以及如何访问和修改列表中的元素。在这个示例中，列表用于存储爬楼方法数。

  3. 循环： 您需要了解如何使用for循环来迭代列表或其他可迭代对象。在这里，循环用于计算每个楼梯的爬楼方法数。

Java 版本

  1. 类和方法： Java中使用类和方法来组织代码。您需要了解如何声明类和方法。在这个示例中，Solution是一个类，climbStairs是一个方法，接受参数n。

  2. 数组： Java中使用数组来存储数据。您需要了解如何声明和初始化数组，以及如何访问和修改数组中的元素。在这个示例中，数组用于存储爬楼方法数。

  3. 循环： 您需要了解如何使用for循环来迭代数组或其他可迭代对象。在这里，循环用于计算每个楼梯的爬楼方法数。

C++ 版本

  1. 类和方法： C++中也可以使用类和方法来组织代码。您需要了解如何声明类和方法。在这个示例中，Solution是一个类，climbStairs是一个方法，接受参数n。

  2. 向量（Vectors）： C++中的向量类似于动态数组，用于存储数据。您需要了解如何声明和初始化向量，以及如何访问和修改向量中的元素。在这个示例中，向量用于存储爬楼方法数。

  3. 循环： 您需要了解如何使用for循环来迭代向量或其他可迭代对象。在这里，循环用于计算每个楼梯的爬楼方法数。

除了上述语言特定的知识，您还需要了解动态规划的基本概念，特别是在这个问题中，它涉及到计算爬楼梯的方法数时如何使用动态规划和Fibonacci序列。熟悉这些语言和算法概念将帮助您理解和编写这个问题的解决方案。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.hqwc.cn/news/138739.html

如若内容造成侵权/违法违规/事实不符，请联系编程知识网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

微信小程序会议OA系统

微信小程序会议OA系统

Flex弹性布局 Flex弹性布局是一种 CSS3 的布局模式&#xff0c;也叫Flexbox。它可以让容器中的元素按一定比例自动分配空间&#xff0c;使得它们在不同宽度、高度等情况下仍能保持整齐和密集不间隙地排列。 在使用Flexbox弹性布局时&#xff0c;首先需要创建一个容器和若干个…
阅读更多...
数据结构----算法--五大基本算法

数据结构----算法--五大基本算法

数据结构----算法–五大基本算法 一.贪心算法 1.什么是贪心算法 在有多个选择的时候不考虑长远的情况&#xff0c;只考虑眼前的这一步&#xff0c;在眼前这一步选择当前的最好的方案 二.分治法 1.分治的概念 分治法&#xff1a;分而治之 将一个问题拆解成若干个解决方式…
阅读更多...
勒索病毒最新变种.halo勒索病毒来袭，如何恢复受感染的数据？

勒索病毒最新变种.halo勒索病毒来袭，如何恢复受感染的数据？

导言&#xff1a; 在当今数字化的世界中&#xff0c; .halo 勒索病毒已经崭露头角&#xff0c;对企业和个人的数据构成严重威胁。本文91数据恢复将深入介绍这种新型病毒的本质&#xff0c;探讨如何恢复被 .halo 勒索病毒加密的数据文件&#xff0c;以及提供一些建议&#xff0c…
阅读更多...
SpringBoot整合Activiti

SpringBoot整合Activiti

SpringBoot集成Activiti7 SpringBoot版本使用2.7.16 <parent><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-parent</artifactId><version>2.7.16</version><relativePath/> <!-- lookup…
阅读更多...
Vue3语法-双向绑定

Vue3语法-双向绑定

点击加入精英计划可以加入 点击名字可以删除 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>Title</title><!-- vue.js --><script src"https://unpkg.com/vue3/dist/vue.glob…
阅读更多...
队列的运行算法

队列的运行算法

1.链队&#xff1a; 插入 删除 打印 取队顶 #include <stdio.h> #include <stdlib.h>typedef struct Qnode{int data;struct Qnode *next; }Qnode,*QuenePtr;typedef struct {QuenePtr front;QuenePtr rear; }LinkQueue; //初始化 void InitQueue(LinkQueue *q){(…
阅读更多...
【LeetCode热题100】-- 45.跳跃游戏II

【LeetCode热题100】-- 45.跳跃游戏II

45.跳跃游戏II 方法&#xff1a;贪心 在具体的实现中&#xff0c;维护当前能够到达的最大下标的位置&#xff0c;记为边界。从左到右遍历数组&#xff0c;到达边界时&#xff0c;更新边界并将跳跃次数加一 在遍历数组时&#xff0c;不访问最后一个元素&#xff0c;因为在访问…
阅读更多...
pytorch代码实现之动态蛇形卷积模块DySnakeConv

pytorch代码实现之动态蛇形卷积模块DySnakeConv

动态蛇形卷积模块DySnakeConv 血管、道路等拓扑管状结构的精确分割在各个领域都至关重要&#xff0c;确保下游任务的准确性和效率。 然而&#xff0c;许多因素使任务变得复杂&#xff0c;包括薄的局部结构和可变的全局形态。在这项工作中&#xff0c;我们注意到管状结构的特殊…
阅读更多...
Linux性能优化--性能追踪：受CPU限制的应用程序（GIMP）

Linux性能优化--性能追踪：受CPU限制的应用程序（GIMP）

10.0 概述 本章包含了一个例子&#xff1a;如何用Linux性能工具在受CPU限制的应用程序中寻找并修复性能问题。 阅读本章后&#xff0c;你将能够&#xff1a; 在受CPU限制的应用程序中明确所有的CPU被哪些源代码行使用。用1trace和oprofile弄清楚应用程序调用各种内部与外部函…
阅读更多...
Leetcode刷题详解——长度最小的子数组

Leetcode刷题详解——长度最小的子数组

1. 题目链接&#xff1a;209. 长度最小的子数组 2. 题目描述&#xff1a; 给定一个含有 n 个正整数的数组和一个正整数 target 。 找出该数组中满足其总和大于等于 target 的长度最小的 连续子数组 [numsl, numsl1, ..., numsr-1, numsr] &#xff0c;并返回其长度**。**如果不…
阅读更多...
【打印机故障】打印时一直显示任务“排队中”无法打印或取消

【打印机故障】打印时一直显示任务“排队中”无法打印或取消

解决办法 一、关闭打印服务 如果打印任务无法取消或者删除&#xff0c;可以先暂停打印机的“服务&#xff0c;关闭”后台处理程序。具体方法如下&#xff1a; 1.在开始菜单搜索框中输入 services.msc或者中文输入“服务”&#xff0c;然后按下 enter 键。 2.从服务列表中选择打…
阅读更多...
程序员大厂之鹅厂探秘

程序员大厂之鹅厂探秘

阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023