随着大数据技术的发展,HDFS作为Hadoop的核心模块之一得到了广泛的应用。为了系统的可靠性,HDFS通过复制来实现这种机制。但在HDFS中每一份数据都有两个副本,这也使得存储利用率仅为1/3,每TB数据都需要占用3TB的存储空间。因此,在保证可靠性的前提下如何提高存储利用率已成为当前HDFS面对的主要问题之一。Hadoop 3.0 引入了纠删码技术(Erasure Coding),它可以提高50%以上的存储利用率,并且保证数据的可靠性。
一、什么是EC
起源
纠删码 (Erasure Code)
纠删码技术起源于通信传输领域,后被逐渐运用到存储系统中。它对数据进行分块,然后计算出一些冗余的校验块。当一部分数据块丢失时,可以通过剩余的数据块和校验块计算出丢失的数据块。
Facebook 的开源项目HDFS-RAID在HDFS之上使用了纠删码技术。HDFS-RAID对属于同一文件的块分组并依次生成校验块,将这些校验块构成独立的文件,并与原始的数据文件一一对应。RaidNode作为一个新的角色被引入进来,它负责从DataNode中读取文件的数据块,计算出校验块, 并写入校验文件中;同时,它还周期性地检查被编码了的文件是否存在块丢失,如有丢失则重新进行计算以恢复丢失的块。
HDFS-RAID的优点是其构建于HDFS之上,不需要修改HDFS本已经复杂的内部逻辑,但缺点也显而易见:校验文件对用户是可见的,存在被误删除的可能;依赖于MySQL和MapReduce来存储元数据和生成校验文件;RaidNode需要周期性地查找丢失的块,加重了NameNode的负担;使用的编解码器性能较差,在实际应用中往往不能满足要求。另外,由于缺乏维护,HDFS已将HDFS-RAID的代码从contrib包中移除,这给使用HDFS-RAID带来不少困难。
发展
2014下半年,英特尔和Cloudera共同提出了将纠删码融入到HDFS内部的想法和设计(HDFS EC),随后吸引了包括Hortonworks、华为、Yahoo!等众多公司的参与,使之成为Hadoop开源社区较为活跃的一个项目。将纠删码融入到HDFS内部带来了诸多好处:它不再需要任何的外部依赖,用户使用起来更为方便;其代码成为HDFS的一部分,便于维护;可以充分利用HDFS的内部机制使性能得到最大程度的优化。纠删码的编解码性能对其在HDFS中的应用起着至关重要的作用,如果不利用硬件方面的优化就很难得到理想的性能。英特尔的智能存储加速库(ISA-L)提供了对纠删码编解码的优化,极大的提升了其性能。
二、EC原理
原理介绍
1. 在存储系统中,纠删码技术主要是通过利用纠删码算法将原始的数据进行编码得到校验,并将数据和校验一并存储起来,以达到容错的目的。其基本思想是将k块原始的数据元素通过一定的编码计算,得到m块校验元素。对于这k+m块元素,当其中任意的m块元素出错(包括数据和校验出错),均可以通过对应的重构算法恢复出原来的k块数据。生成校验的过程被成为编码(encoding),恢复丢失数据块的过程被称为解码(decoding)。
Reed-Solomon Codes缩写为RS码,使用复杂的线性代数运算来生成多个奇偶校验块,因此可以容忍多个数据块故障。RS码在使用的时候需指定2个参数RS(n, m),n代表的是数据块的数量,m代表的是校验块的数量,校验块由数据块编码产生。
2. RS编码的编码与解码原理如图1所示。编码时,利用生成矩阵B与数据列向量D的乘积得到信息列向量D+C;重构时,利用现存的信息列向量Survivors与对应的逆矩阵B'-1 乘积得到原数据列向量D,从而达到恢复原数据的目的。
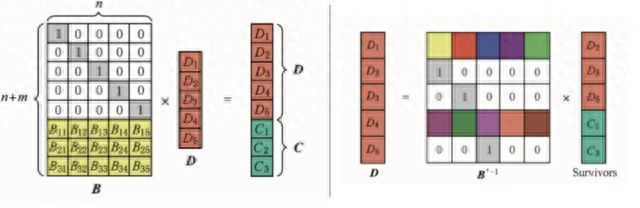
图1 RS编码的编码与重构原理
举例
举个例子:
比如:我们有 7、8、9 三个原始数据,通过矩阵乘法,计算出来两个校验数据 50、122。这时原始数据加上校验数据,一共五个数据:7、8、9、50、122,可以任意丢两个,然后通过算法进行恢复。
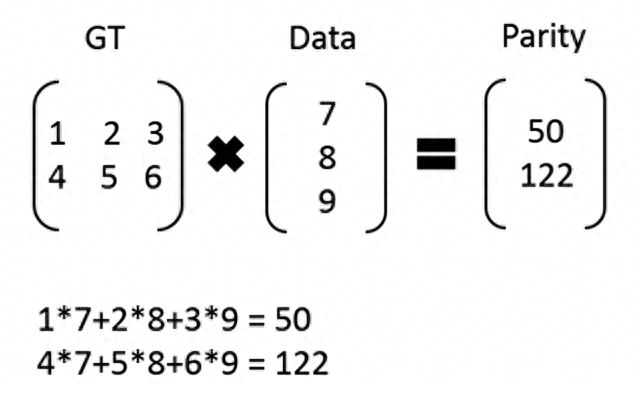
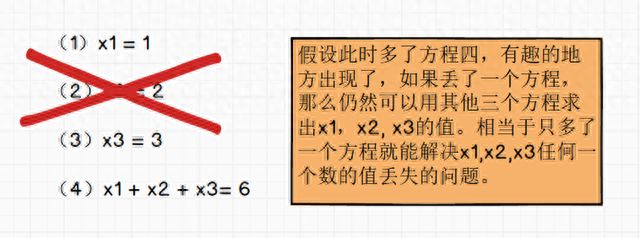
我们再举个简单的例子:


三、HDFS EC方案
连续布局
对HDFS的一个普通文件来说,构成它的基本单位是块。对于EC模式下的文件,构成它的基本单位为块组。块组由一定数目的数据块加上生成的校验块放一起构成。以RS(6,3)为例,每一个块组包含1-6个数据块,以及3个校验块。进行EC编码的前提是每个块的长度一致。如果不一致,则应填充0。
数据被依次写入一个块中,一个块写满之后再写入下一个块,数据的这种分布方式被称为连续布局。在一些分布式文件系统如QFS和Ceph中,广泛使用另外一种布局:条形布局。条(stripe)是由若干个相同大小单元(cell)构成的序列。在条形布局下,数据被依次写入条的各个单元中,当条被写满之后就写入下一个条,一个条的不同单元位于不同的数据块中。
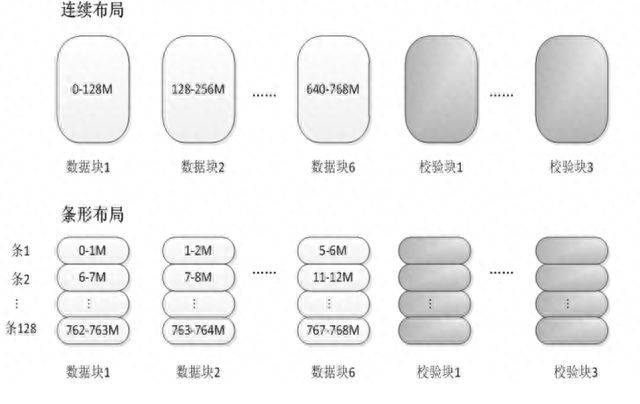
文件数据被依次写入块中,一个块写满之后再写入下一个块,这种分布方式称为连续布局。
优点:
- 容易实现
- 方便和多副本存储策略进行转换
缺点:
- 需要客户端缓存足够的数据块
- 不适合存储小文件
条形布局
条(stripe)是由若干个相同大小的单元(cell)构成的序列。文件数据被依次写入条的各个单元中,当一个条写满之后再写入下一个条,一个条的不同单元位于不同的数据块中。这种分布方式称为条形布局。
优点:
- 客户端缓存数据较少
- 无论文件大小都适用
缺点:
- 会影响一些位置敏感任务的性能,因为原先在一个节点上的块被分散到了多个不同的节点上。
- 和多副本存储策略转换比较麻烦。
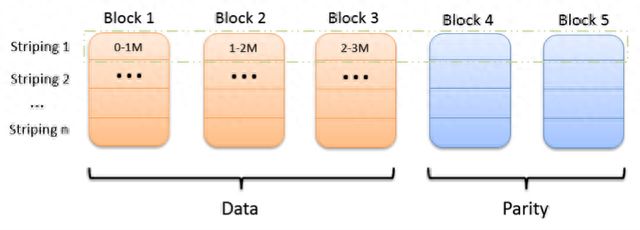
布局方案选择
对HDFS EC来说,首要的问题是选择什么样的布局方式。连续布局实现起来较为容易,但它只适合较大的文件。另外,如果让client端直接写一个连续布局文件需要缓存下足够的数据块,然后生成校验块并写入,以RS(6,3),blockSize=128M为例,client端需要缓存1.12G的数据,这点决定了连续布局的文件更适合由普通文件转化而来,而条形布局就不存在上述缺点。由于一个条的单元往往较小(通常为64K或1M),因此无论文件大小,条形布局都可以为文件节省出空间。client端在写完一个条的数据单元后就可以计算出校验单元并写出,因此client端需要缓存的数据很少。条形布局的一个缺点是会影响一些位置敏感任务的性能,因为原先在一个节点上的一个块被分散到了多个不同的节点上。
HDFS最初就是为较大文件设计的分布式文件系统,但随着越来越多的应用将数据存储于HDFS上,HDFS的小(即小于1个块组)文件数目越来越多,而且它们所占空间的比率也越来越高。以Cloudera一些较大客户的集群为例,小文件占整个空间的比例在36-97%之间。
基于以上分析,HDFS EC优先考虑对条形布局的支持。设计与实现也主要围绕已经实现了的条形布局展开。
四、EC的优势与劣势
优势
纠删码技术作为一门数据保护技术,自然有许多的优势,首先可以解决的就是目前分布式系统,云计算中采用副本来防止数据的丢失。副本机制确实可以解决数据丢失的问题,但是翻倍的数据存储空间也必然要被消耗,这一点却是非常致命的。EC技术的运用就可以直接解决这个问题。
劣势
EC技术的优势确实明显,但是他的使用也是需要一些代价的,一旦数据需要恢复,他会造成2大资源的消耗:
1、网络带宽的消耗,因为数据恢复需要去读其他的数据块和校验块。
2、进行编码,解码计算需要消耗CPU资源。
就是既耗网络又耗CPU。
总结
纠删码技术作为一门数据保护技术,自然有许多的优势。将纠删码技术融入到HDFS中,可以保证在同等(或者更高)可靠性的前提下,将存储利用率提高了一倍。同样的集群用户可以存储两倍的数据,这将大大减少用户硬件方面的开销。
对于EC,最好的选择是用于冷数据集群,有下面2点原因:
1. 冷数据集群往往有大量的长期没有被访问的数据,体量确实很大,采用EC技术,可以大大减少副本数。
2.冷数据集群基本稳定,耗资源量少,所以一旦进行数据恢复,将不会对集群造成大的影响。
出于上述2种原因,冷数据集群是一个很好的选择。