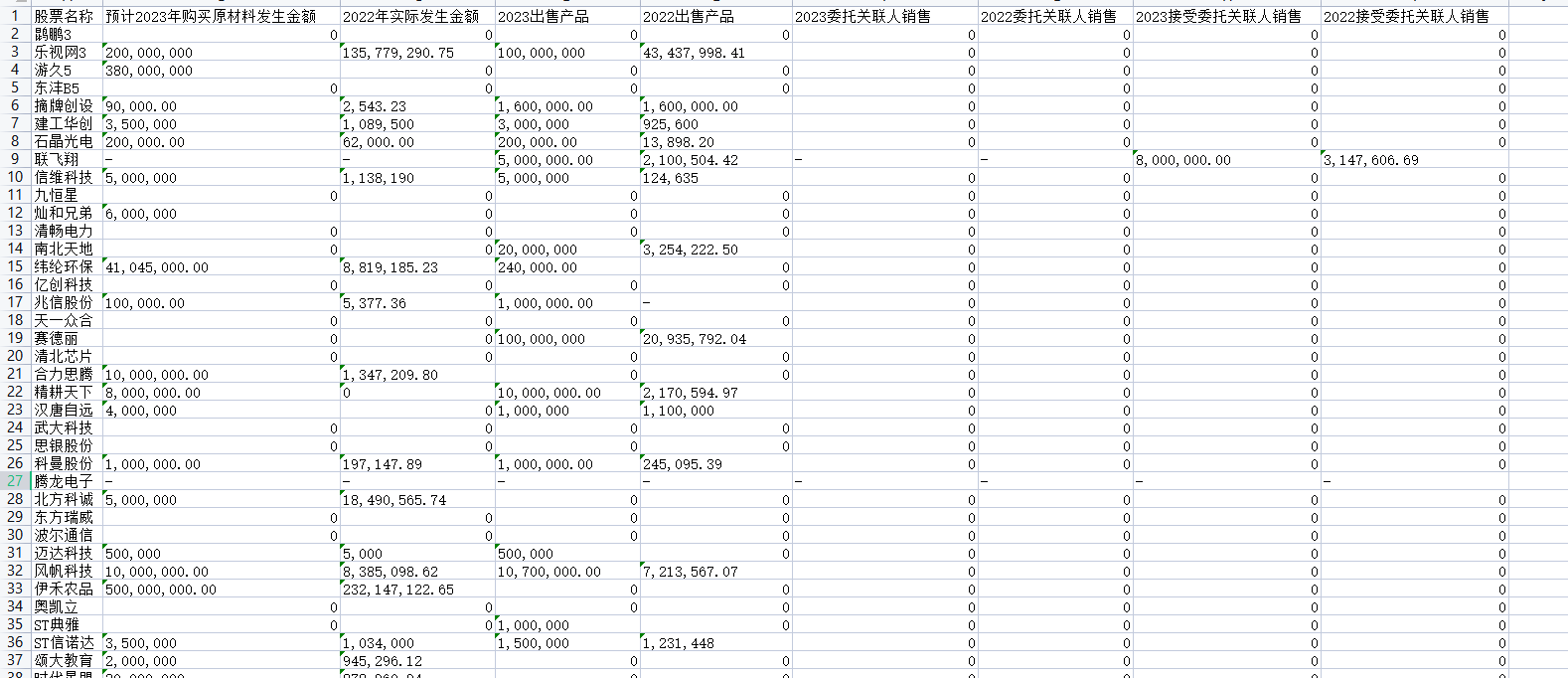
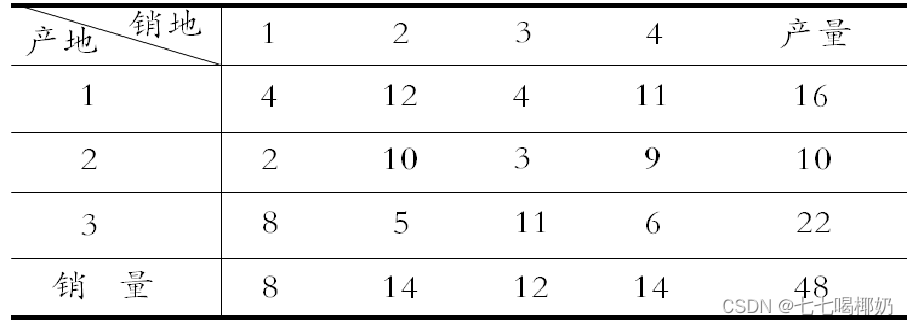
某部门有三个生产同一产品的工厂(产地),生产的产品运往四个销售点(销地)出售,各个工厂的生产量、各销地的销量(单位:吨)、从各个工厂到各个销售点的单位运价(元/吨)如下表,研究如何调运才能使得总运费最小。
【数学模型】
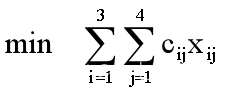
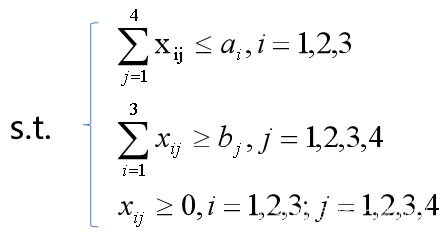
如果此模型扩展到有50个产地和100个销售地的规模,从理解问题的角度看,就是让i=1,2,…,50;j=1,2,…,100就行了,但是为了让计算机处理,还是按照前面的一行一个语句逐字逐句地输入,工作量就太大了。Lingo就有节约时间的输入方式,且计算机也能理解,那就是集合式输入法。
1、集合(下标)部分
这一部分定义集合(数组)以及属性(也就是只与这些下表有关的决策变量(符号变量))
规范格式
sets:
chandi/1,2,3/:a;
endsets
这样就定义了集合chandi={1,2,3},对应的属性(只与这个下标有关的量)a,于是上述语句就定有了a(1),a(2),a(3)这三个变量名(可能是决策变量,也可能是已知量),表示是三个产地的产量。
在计算过程中,只要出现chandi,就表示按顺序取值于1,2,3。
上面的集合定义,如果集合元素比较多,则采用下面的定义方式
sets:
chandi/1..3/:a;
endsets
如果是
sets:
chandi/1..50/:a;
endsets
那就定义了50个变量名a(1),a(2),…,a(50)。
而上例中,有三个产地(及其产量),四个销售地(及其相应的销量),则可以如下定义
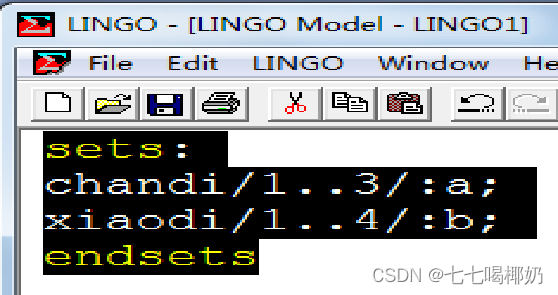
这样就定义了chandi这个集合,与这个集合有关的属性a,xiaodi这个集合,与这个集合有关的属性b,直接定义了a(1),a(2),a(3),b(1),b(2),b(3),b(4),这样直接定义的集合称为基本集合。
上例中,还有形如x12,c12这样的变量名如何定义呢?这样的变量既与产地有关,又与销地有关,于是就由chandi这个集合与xiaodi这个集合联合生成一个笛卡尔集,称为派生集合(关联变量的下标范围):
sets:
chandi/1..3/:a;
xiaodi/1..4/:b;
link(chandi,xiaodi):x,c;
endsets
这样就增加了一个新的集合link,它由chandi和xiaodi两个集合生成,从数学看
![]()
与之有关的属性为x,c,就定义了如下变量名
x(1,1),x(1,2),x(1,3),x(1,4) x(2,1),x(2,2),x(2,3),x(2,4) x(3,1),x(3,2),x(3,3),x(3,4)
c(1,1),c(1,2) ,c(1,3),c(1,4) c(2,1),c(,2,2),c(2,3),c(2,4) c(3,1),c(3,2) ,c(3,3),c(3,4)
2、数据部分
这部分格式:
data:
a=16,10,22;
b=8,14,12,14;
c=4 12 4 112 10 3 98 5 11 6;
enddata
以”data:”开始,以“enddata”结束。不管变量是行还是列,都采用行写,行元素之间可以逗号“,”隔开,也可以空格隔开。而矩阵输入时,先行后列,每行输入完毕,就回车(enter),再输入一行,直到输入完毕,再分号“;”每个变量的数据输入完毕,都用分号“;”结束。
3、模型部分
这部分要把模型的约束和目标函数全部反应出来,如下约束
即对每个产地i(i=1,2,3)来说,从这里运往各个销地(j=1,j=2,j=3,j=4)的运输量之和:x(i,1)+x(i,2)+x(i,3)+x(i,4)不超过产地i 的产量a(i),即x(i,1)+x(i,2)+x(i,3)+x(i,4)<= a(i), i=1,2,3
翻译为lingo程序语言:
@for(chandi(i):@sum(xiaodi(j): x(i,j))<=a(i));
实际就是其它程序语言的for循环结构的打包形式!
按照上面的分析方法,对每个销售地来说,调运量总和必须满足销售需求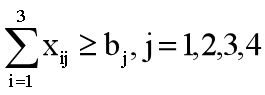
翻译为lingo程序语言为
@for(xiaodi(j): @sum(chandi(i): x(i,j)) >= b(j) );
目标是将所有线路的运费求和,并使之最小化,即
翻译为Lingo程序语言,就是
min= @sum( link(i,j): c(i,j)*x(i,j));
注意:以上写法中,注意括号匹配,分号结束。
4、初始值部分
在针对线性规划时,这个部分不需要。但是针对非线性规划,这个部分就有必要了,给出决策值的迭代始点,更容易找到局部最优解,同时,给出不同的初始值,可以尝试寻找不同的局部最优解,然后加以比较,找到较好的局部最优解,作为全局最优解使用。格式为init开始,endinit结束。
举例:
初始值设为x1=0,x2=5
设x1=5,x2=1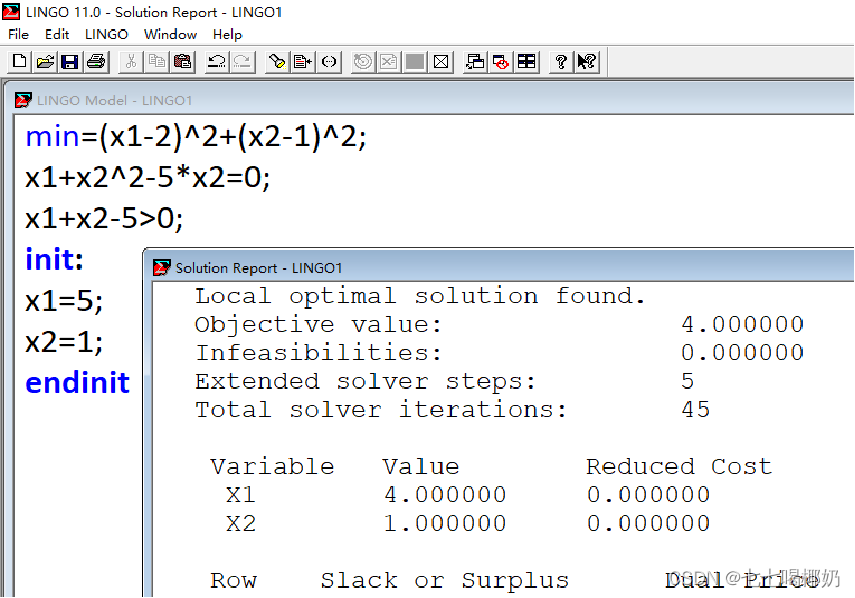
本例子的总代码
sets:
chandi/1..3/:a;
xiaodi/1..4/:b;
link(chandi,xiaodi):x,c;
endsets
data:
a=16,10,22;
b=8,14,12,14;
c=4 12 4 112 10 3 98 5 11 6;
enddata
@for(chandi(i):@sum(xiaodi(j):x(i,j))<a(i));
@for(xiaodi(j):@sum(chandi(i):x(i,j))>b(j));
min=@sum(link(i,j):x(i,j)*c(i,j));