A. Rudolph and Cut the Rope

只需要按照钉子距离的高度$a_i$和绳子的长度$b_i$的差值进行排序即可

代码

int n;
pii a[N];
bool cmp(pii a,pii b)
{return a.x-a.y<b.x-b.y;
}void solve()
{cin>>n;for(int i=1;i<=n;i++)cin>>a[i].x>>a[i].y;sort(a+1,a+1+n,cmp);reverse(a+1,a+1+n);int res=0;for(int i=1;i<=n;i++){if(a[i].x<=a[i].y){break;}res++;}cout<<res<<endl;
}

B. Rudolph and Tic-Tac-Toe

模拟即可

代码

void solve()
{int n=3;for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)cin>>s[i][j];for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){if(s[i][j]==s[i][j+1]&&s[i][j+1]==s[i][j+2]&&s[i][j]!='.'){cout<<s[i][j]<<endl;return;}if(s[i][j]==s[i+1][j]&&s[i+1][j]==s[i+2][j]&&s[i][j]!='.'){cout<<s[i][j]<<endl;return;}if(s[i][j]==s[i+1][j+1]&&s[i+1][j+1]==s[i+2][j+2]&&s[i][j]!='.'){cout<<s[i][j]<<endl;return;}if(s[i][j]==s[i+1][j-1]&&s[i+1][j-1]==s[i+2][j-2]&&s[i][j]!='.'){cout<<s[i][j]<<endl;return;}}}cout<<"DRAW"<<endl;
}

C. Rudolf and the Another Competition

统计出每个人的过题的数量$x_i$和罚时$t_i$然后依次先对比过题数然后再对比罚时即可

void solve()
{cin>>n>>m>>t;vector<pii>p(n+10);int res=0;for(int i=0;i<n;i++){p[i].x=p[i].y=0;vector<int>a;int s=0;for(int j=0;j<m;j++){int x;cin>>x;a.push_back(x);}sort(a.begin(),a.end());for(int j=0;j<m;j++){s=s+a[j];if(s<=t){p[i].x+=1;p[i].y+=s;}	}if(i>0){if((p[0].x<p[i].x)||(p[0].x==p[i].x&&p[i].y<p[0].y))res++;}}cout<<res+1<<endl;}

D. Rudolph and Christmas Tree

先统计所有三角形的面积，然后减去重叠部分即可，重叠部分可以根据初中学过的相似三角形定理对应边成比例即可

void solve()
{cin>>n>>d>>h;for(int i=1;i<=n;i++)cin>>y[i];sort(y+1,y+1+n);double s=n*d*h*0.5;for(int i=2;i<=n;i++){int v=h+y[i-1];if(v>y[i]){double x=v-y[i]*1.0;double t=x/h*d*x*0.5;s-=t;}}printf("%f\n",s);
}

E2. Rudolf and Snowflakes (hard version)

根据样例中的图解

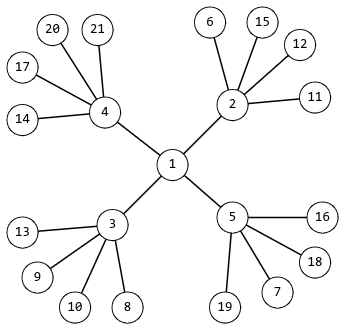
节点个数假设为$n$

$n=1+4^1+4^2=21$

我们假设他有$k$个子节点，会扩展$x$次那我们可以推出一个方程

$n=1+k+k^2+....+k^x$

所以只要将$n$分解成多项式即可

我们可以看出这个具有单调性，所以可以利用二分来快速求得答案

先枚举指数$x\in [2,60]$ 然后再二分$k$即可

void solve()
{cin>>n;for(int i=2;i<=60;i++){int l=1,r=n+1;auto check=[&](int x){int s=0,t=1;for(int j=0;j<=i;j++){s+=t;if(s>inf)s=inf;if((__int128_t)t*x>inf)t=inf;else t*=x;}return s;};while(l+1<r){int mid=l+r>>1;if(check(mid)>=n)r=mid;else l=mid;}if(check(r)==n){cout<<"YES"<<endl;return;}}cout<<"NO"<<endl;return;
}int mid=l+r>>1;if(check(mid)>=n)r=mid;else l=mid;}if(check(r)==n){cout<<"YES"<<endl;return;}}cout<<"NO"<<endl;return;
}