文章目录
- 题目
- 标题和出处
- 难度
- 题目描述
- 要求
- 示例
- 数据范围
- 解法一
- 思路和算法
- 代码
- 复杂度分析
- 解法二
- 思路和算法
- 代码
- 复杂度分析
题目
标题和出处
标题:最大二叉树
出处:654. 最大二叉树
难度
5 级
题目描述
要求
给定一个没有重复元素的整数数组 nums \texttt{nums} nums。最大二叉树可以用下面的算法从 nums \texttt{nums} nums 递归地构建:
- 创建一个根结点,其值为 nums \texttt{nums} nums 中的最大值。
- 递归地在最大值左边的子数组前缀上构建左子树。
- 递归地在最大值右边的子数组后缀上构建右子树。
返回从 nums \texttt{nums} nums 构建的最大二叉树。
示例
示例 1:
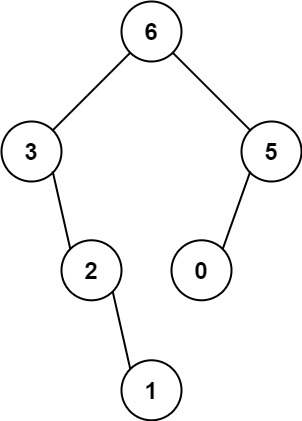
输入: nums = [3,2,1,6,0,5] \texttt{nums = [3,2,1,6,0,5]} nums = [3,2,1,6,0,5]
输出: [6,3,5,null,2,0,null,null,1] \texttt{[6,3,5,null,2,0,null,null,1]} [6,3,5,null,2,0,null,null,1]
解释:递归调用如下所示:
- [3,2,1,6,0,5] \texttt{[3,2,1,6,0,5]} [3,2,1,6,0,5] 中的最大值是 6 \texttt{6} 6,左边部分是 [3,2,1] \texttt{[3,2,1]} [3,2,1],右边部分是 [0,5] \texttt{[0,5]} [0,5]。
- [3,2,1] \texttt{[3,2,1]} [3,2,1] 中的最大值是 3 \texttt{3} 3,左边部分是 [] \texttt{[]} [],右边部分是 [2,1] \texttt{[2,1]} [2,1]。
- 空数组,无子结点。
- [2,1] \texttt{[2,1]} [2,1] 中的最大值是 2 \texttt{2} 2,左边部分是 [] \texttt{[]} [],右边部分是 [1] \texttt{[1]} [1]。
- 空数组,无子结点。
- 只有一个元素,所以子结点是一个值为 1 \texttt{1} 1 的结点。
- [0,5] \texttt{[0,5]} [0,5] 中的最大值是 5 \texttt{5} 5,左边部分是 [0] \texttt{[0]} [0],右边部分是 [] \texttt{[]} []。
- 只有一个元素,所以子结点是一个值为 0 \texttt{0} 0 的结点。
- 空数组,无子结点。
- [3,2,1] \texttt{[3,2,1]} [3,2,1] 中的最大值是 3 \texttt{3} 3,左边部分是 [] \texttt{[]} [],右边部分是 [2,1] \texttt{[2,1]} [2,1]。
示例 2:
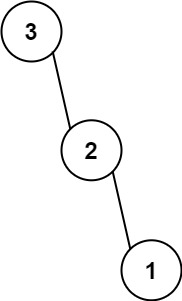
输入: nums = [3,2,1] \texttt{nums = [3,2,1]} nums = [3,2,1]
输出: [3,null,2,null,1] \texttt{[3,null,2,null,1]} [3,null,2,null,1]
数据范围
- 1 ≤ nums.length ≤ 1000 \texttt{1} \le \texttt{nums.length} \le \texttt{1000} 1≤nums.length≤1000
- 0 ≤ nums[i] ≤ 1000 \texttt{0} \le \texttt{nums[i]} \le \texttt{1000} 0≤nums[i]≤1000
- nums \texttt{nums} nums 中的所有整数各不相同
解法一
思路和算法
由于给定的数组中的整数各不相同,因此可以唯一地确定最大二叉树的根结点,以及每个子树中的根结点。
遍历数组得到最大值所在的下标,使用该下标处的值创建根结点,使用该下标左边的子数组创建左子树,使用该下标右边的子数组创建右子树。对于左边的子数组和右边的子数组,使用同样的方法构造最大子二叉树。
上述构造最大二叉树的过程是一个递归分治的过程。将二叉树分成根结点、左子树和右子树三部分,首先构造左子树和右子树,然后构造原始二叉树,构造左子树和右子树是原始问题的子问题。
分治的终止条件是子数组为空,此时构造的子树为空。当子数组不为空时,子数组中一定存在整数,因此存在最大值,得到最大值所在的下标之后,即可得到左子树和右子树对应的子数组,然后递归地构造左子树和右子树。
实现方面,为了降低时间复杂度和空间复杂度,每个子数组使用开始下标和结束下标确定,当开始下标大于结束下标时表示子数组为空,则不用新建数组和复制数组元素。
代码
class Solution {public TreeNode constructMaximumBinaryTree(int[] nums) {return constructMaximumBinaryTree(nums, 0, nums.length - 1);}public TreeNode constructMaximumBinaryTree(int[] nums, int start, int end) {if (start > end) {return null;}int maximumValueIndex = getMaximumValueIndex(nums, start, end);TreeNode root = new TreeNode(nums[maximumValueIndex]);root.left = constructMaximumBinaryTree(nums, start, maximumValueIndex - 1);root.right = constructMaximumBinaryTree(nums, maximumValueIndex + 1, end);return root;}public int getMaximumValueIndex(int[] nums, int start, int end) {int maximumValueIndex = start;for (int i = start + 1; i <= end; i++) {if (nums[i] > nums[maximumValueIndex]) {maximumValueIndex = i;}}return maximumValueIndex;}
}
复杂度分析
-
时间复杂度: O ( n 2 ) O(n^2) O(n2),其中 n n n 是数组 nums \textit{nums} nums 的长度,即二叉树的结点数。二叉树有 n n n 个结点,需要分别构造 n n n 个子树,对于每个子树最多需要 O ( n ) O(n) O(n) 的时间定位到根结点和 O ( 1 ) O(1) O(1) 的时间构造,因此总时间复杂度是 O ( n 2 ) O(n^2) O(n2)。
-
空间复杂度: O ( n ) O(n) O(n),其中 n n n 是数组 nums \textit{nums} nums 的长度,即二叉树的结点数。空间复杂度主要是递归调用的栈空间,取决于二叉树的高度,最坏情况下二叉树的高度是 O ( n ) O(n) O(n)。
解法二
思路和算法
注意到从给定的数组 nums \textit{nums} nums 构造的最大二叉树中,结点值的左右相对位置和数组 nums \textit{nums} nums 中的左右相对位置保持一致。对于数组 nums \textit{nums} nums 中的任意两个元素 x x x 和 y y y,其中 x x x 在 y y y 的左侧,当 x > y x > y x>y 时 y y y 在 x x x 的右子树中,当 x < y x < y x<y 时 x x x 在 y y y 的左子树中。
对于数组 nums \textit{nums} nums 中的每个整数,为了得到该结点的父结点,需要在数组 nums \textit{nums} nums 中找到比该整数大的最小整数。可以使用单调栈,单调栈存储结点,满足从栈底到栈顶的结点值单调递减。
从左到右遍历数组 nums \textit{nums} nums,对于每个整数,执行如下操作。
-
如果栈不为空且栈顶结点值小于当前整数,则将栈顶结点出栈,由于结点出栈的顺序对应数组中从右到左的顺序,因此如果有多个结点出栈,则每次将出栈结点的右子结点设为上一个出栈的结点。重复该操作,直到栈为空或者栈顶结点值大于当前整数时,停止该操作。
-
用当前整数创建结点,将当前结点的左子结点设为最后一个出栈的结点,然后将当前结点入栈。
遍历结束后,每个结点的左子树构造完毕,除了栈内的结点以外的每个结点的右子树也构造完毕。栈内的每个结点的右侧都不存在更大的整数,因此除了根结点以外,每个结点都是其父结点的右子结点。栈底结点为值最大的结点,因此作为根结点。当栈内结点数大于 1 1 1 时,每次将一个结点出栈,然后将新的栈顶结点的右子结点设为出栈结点。当栈内只剩 1 1 1 个结点时,该结点即为最大二叉树的根结点,将该结点出栈并返回。
上述做法的正确性可以根据单调栈的性质和操作过程得到。对于整数 x x x,考虑如下情况。
-
如果 x x x 是数组中的最大整数,则结点 x x x 即为根结点。
-
如果只有 x x x 的一侧存在比 x x x 大的整数,则比 x x x 大的最小整数对应的结点即为结点 x x x 的父结点。
-
如果 x x x 的两侧都存在比 x x x 大的整数,用 y y y 表示 x x x 的左侧的整数中比 x x x 大的最小整数,用 z z z 表示 x x x 的右侧的整数中比 x x x 大的最小整数,则 x x x 的父结点值为 y y y 和 z z z 中的最小整数,考虑 y y y 和 z z z 的大小关系。
-
如果 y < z y < z y<z,则当遍历到 z z z 时,结点 x x x 和 y y y 依次出栈,将结点 y y y 的右子结点设为结点 x x x,结点 z z z 的左子结点设为结点 y y y,此时结点 x x x 的父结点为结点 y y y。
-
如果 y > z y > z y>z,则当遍历到 z z z 时,结点 x x x 出栈,将结点 z z z 的左子结点设为结点 x x x,此时结点 x x x 的父结点为结点 z z z。
-
以下是示例 1 的构造过程,其中 nums = [ 3 , 2 , 1 , 6 , 0 , 5 ] \textit{nums} = [3,2,1,6,0,5] nums=[3,2,1,6,0,5]。
-
下标 0 0 0 处的整数是 3 3 3,创建结点 3 3 3 并入栈, stack = [ 3 ] \textit{stack} = [3] stack=[3],其中左边为栈底,右边为栈顶,栈内元素为结点,此处用数字表示结点且省略父结点和子结点的关系。
-
下标 1 1 1 处的整数是 2 2 2,创建结点 2 2 2 并入栈, stack = [ 3 , 2 ] \textit{stack} = [3, 2] stack=[3,2]。
-
下标 2 2 2 处的整数是 1 1 1,创建结点 1 1 1 并入栈, stack = [ 3 , 2 , 1 ] \textit{stack} = [3, 2, 1] stack=[3,2,1]。
-
下标 3 3 3 处的整数是 6 6 6,由于栈内的结点 1 1 1、 2 2 2、 3 3 3 的结点值都小于 6 6 6,因此需要将结点出栈并更新每个结点的子结点。
-
依次将结点 1 1 1、 2 2 2、 3 3 3 出栈并更新每个结点的右子结点,将结点 2 2 2 的右子结点设为结点 1 1 1,将结点 3 3 3 的右子结点设为结点 2 2 2。
-
创建结点 6 6 6,将结点 6 6 6 的左子结点设为结点 3 3 3,将结点 6 6 6 入栈, stack = [ 6 ] \textit{stack} = [6] stack=[6]。
-
-
下标 4 4 4 处的整数是 0 0 0,创建结点 0 0 0 并入栈, stack = [ 6 , 0 ] \textit{stack} = [6, 0] stack=[6,0]。
-
下标 5 5 5 处的整数是 5 5 5,由于栈内的结点 0 0 0 的结点值小于 5 5 5,因此需要将结点出栈并更新每个结点的子结点。
-
将结点 0 0 0 出栈。
-
创建结点 5 5 5,将结点 5 5 5 的左子结点设为结点 0 0 0,将结点 5 5 5 入栈, stack = [ 6 , 5 ] \textit{stack} = [6, 5] stack=[6,5]。
-
-
遍历结束,此时栈内有 2 2 2 个结点。将结点 5 5 5 出栈,将结点 6 6 6 的右子结点设为结点 5 5 5。
-
栈内剩余的结点 6 6 6 即为最大二叉树的根结点,将结点 6 6 6 出栈并返回。
代码
class Solution {public TreeNode constructMaximumBinaryTree(int[] nums) {Deque<TreeNode> stack = new ArrayDeque<TreeNode>();int length = nums.length;for (int i = 0; i < length; i++) {int num = nums[i];TreeNode prev = null;while (!stack.isEmpty() && stack.peek().val < num) {TreeNode curr = stack.pop();curr.right = prev;prev = curr;}TreeNode node = new TreeNode(num);node.left = prev;stack.push(node);}while (stack.size() > 1) {TreeNode curr = stack.pop();stack.peek().right = curr;}return stack.pop();}
}
复杂度分析
-
时间复杂度: O ( n ) O(n) O(n),其中 n n n 是数组 nums \textit{nums} nums 的长度,即二叉树的结点数。需要遍历数组 nums \textit{nums} nums,每个结点最多入栈和出栈各一次,更新每个结点的子结点的时间是 O ( 1 ) O(1) O(1),因此总时间复杂度是 O ( n ) O(n) O(n)。
-
空间复杂度: O ( n ) O(n) O(n),其中 n n n 是数组 nums \textit{nums} nums 的长度,即二叉树的结点数。空间复杂度主要是栈空间,栈内元素个数不超过 n n n。