1 介绍

1.1 概述

运动控制（Motion control）是自动化技术的一部份，是指让系统中的可动部份以可控制的方式移动的系统或是子系统。
机器的位置或是速度一般会由液压泵、线性致动器或是电动马达（例如servo）之类的设备所控制。

1.2 运动控制的基本架构

• 运动控制器（motion controller）可以产生控制目标（理想的输出或是运动廓线），或是闭环控制系统中要配合位置或是速度回授形成回授控制[2]
• 驱动器或是放大器可以将运动控制器的控制信号转换为可以提供给致动器的能量。较新型的“智能性”驱动器可以利用驱动器进行速度控制或是位置控制，因此控制可以更加的精准。
• 原动机或是致动器，例如液压泵浦、液压缸、线性致动器或是马达可以实际使物体移动的设备。
• 若是闭回授控制，会需要许多的感测器（如旋转编码器、解角器或是霍尔元件将致动器的位置或是速度的资讯传送回控制器或是驱动器，才能达成回授控制。
• 机械元件让致动器的输出转换为实际需要的输出，机械元件有齿轮、驱动轴、滚珠螺杆、驱动皮带、连杆机构以及线性或是旋转的轴承。

1.3 常见的控制功能

• 速度控制。
• 位置（点对点）控制：有多种计算运动轨迹的方法。这些通常基于移动的速度分布，例如三角形分布、梯形分布或 S 曲线分布。
• 压力、力或是力矩的控制。
• 阻抗控制：这种类型的控制适用于环境交互和对象操纵，例如机器人技术。
• 电子齿轮（或凸轮轮廓）：从动轴的位置和主动轴位置之间的关系可以用数学函数来表示。简单的是一系统中有二个滚筒，但其转速需维持一定比例（即为电子齿轮）。电子凸轮的情形类似凸轮，从动轴的位置是主动轴位置的数学函数（例如主动轴150至180度时，从动轴从0度转至30度，180至210度时，从动轴从30度转至0度，主动轴在其他位置时，从动轴维持在0度的位置）。

1.4 运动控制研究的问题分类

位置变化问题

其特征是被控对象空间位置发生改变，我们称之为第一类运动控制问题。

对第一类运动控制问题而言，被控对象的运动特征是：空间位置发生变化，在位置变化的过程中被控对象的速度或加速度发生变化。解决第一类运动问题的要点是根据牛顿运动学理论与电机拖动的基本理论，按照被控制对象的空间运动轨迹，把被控对象的运动轨迹分解为空间坐标系的坐标变化。然后通过对坐标系坐标的变化进行分析，建立描述运动轨迹的方程；根据牛顿力学和运动学理论，第一类运动控制问题被转化为路程、速度、加速度和时间等几个参数关系的分析问题。表述运动轨迹有三个要素：起始点、终止点及两点之间的连接曲线；平面二维运动是空间三维运动的特例，直线一维运动则是平面二维运动的特例。

周期式旋转速度变化问题

由于某一类物理量（如温度、压力、流量、转矩等）而迫使电机转速随负载的变化而变化，以满足温度、压力、流量、转矩等恒定的目的。我们把这类运动控制问题称为第二类运动控制问题。

第二类运动控制问题是由具体的、实际生产问题演化派生出来的。例如，某小区的生活供水问题，由于用户的用水量是随机变化的，要确保用户的用水品质，从控制的角度就需要保持供水压力恒定；再例如，要求某温室的温度恒定，其问题的实质是在研究循环风机通风量大小的问题，室内温度与设定的温度差决定着通风风机通风量的大小，温差越大，要求风机的循环风量越大，也就是电机的转速越高，而温差越小，要求循环风量越小，电机的转速越低。从第二类运动问题对控制系统的要求看，对这类对象的控制往往是与某些特定的物理量（温度、压力、流量等）相关联的，其前提条件是维持该物理量不变或者按照规定的规律变化。通过前述分析发现，这些要求都能与电机的转速建立起函数关系，因此第二类运动控制问题就转变为电机驱动速度实时控制的问题。工农业生产与人们日常生活中广泛应用的诸如风机、水泵、空调压缩机等负载都属于这个类型。据有关统计资料表明，这类负载占据了整个工业生产能量消耗的 50%～60%。鉴于水泵、风机、压缩机电机的控制都是单向、周期的，因此这一类问题可以归纳为单轴运动控制的周期式旋转控制问题。

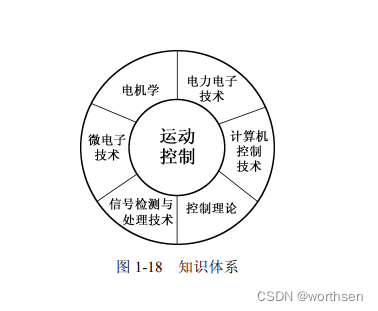
1.5 知识体系

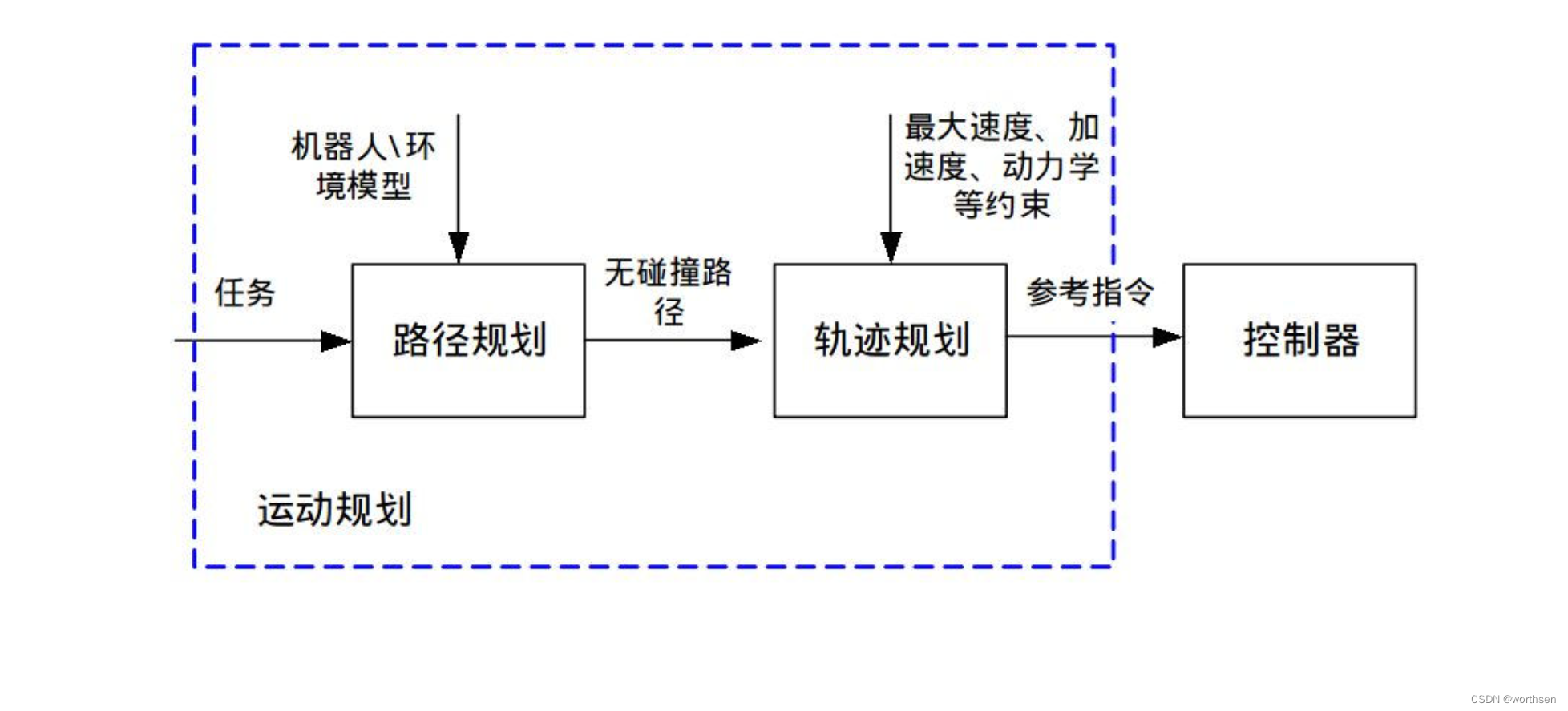
1.6 路径规划 和 轨迹规划区别与联系

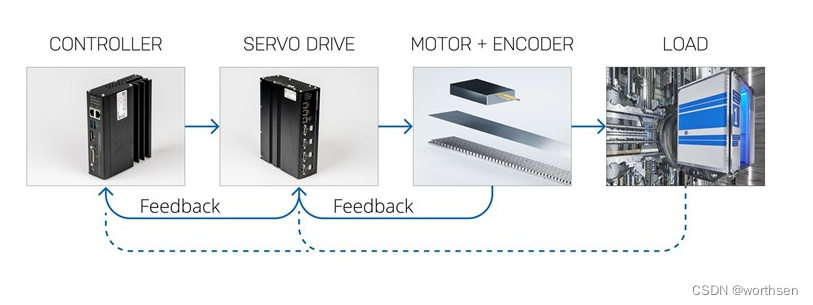
1.7 运动控制系统

2 《运动控制系统》[班华 李长友 主编] 摘要

1 绪论

1.1 运动控制研究的问题

1.1.1 第一类运动控制问题

凡是被控制对象的空间位置或者轨迹随着运动而发生改变的运动控制系统，都属于第一类运动控制系统。
因为第一类运动控制在理论上完全遵循牛顿力学定律和运动学原则，为了便于对第一类运动控制问题进行分析与解析，我们把第一类运动控制问题转化为物理学的牛顿运动学问题。把被控对象的研究转化为被控物体在笛卡儿坐标系中的位移、速度及加速度与运动时间的关系上。

第一类运动控制的核心是研究被控制对象的运动轨迹，分析运动路径、运动速度、运动对象的加速度（力或者力矩）与时间的联系，利用牛顿定律建立求解方程，从而探求快速、平稳、精确的控制方法和控制策略。第一类运动控制问题均可使用典型曲线特征点对其位置轨迹或者速度轨迹加以描述，因此运动轨迹的研究实质上是分析各类运动轨迹的特征点，找出其规律性。典型的第一类运动问题有如下几类。

1．一维运动
一维运动的特点是运动形式十分简单。其基本运动形式分为两类：一是直线运动，二是旋转运动；此外，还可以是两类基本运动的复合，如图 1-1 所示。


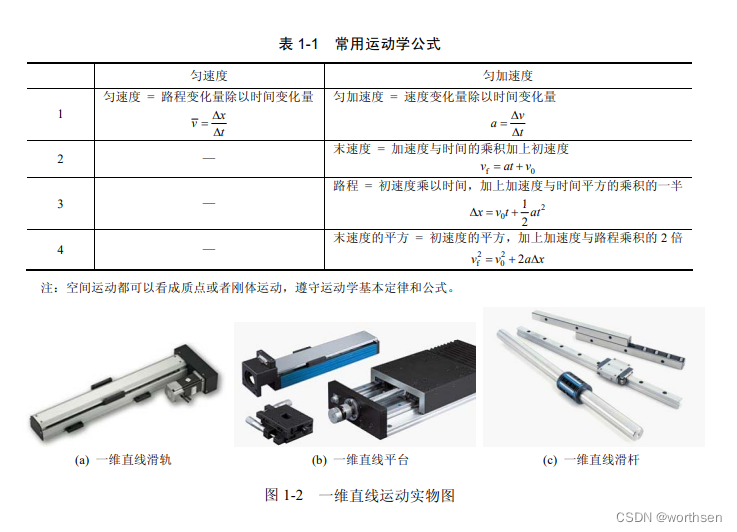
2．二维运动
把两个一维直线运动平台互相垂直搭接在一起，就组成了一个二维运动平台。显然，一维运动是二维运动的特例，二维运动是一维直线运动的平面化，是一维轨迹的延伸和拓展。二维运动平台由两个一维平台构成，每一个一维平台分别代表一个坐标轴，其中与坐标系 x 轴重合的那个平台定义为 x 轴，它的轨迹变化就是 x 轴坐标变化；另一个平台与 y 轴重合，被定义为 y 轴。二维运动轨迹可以是直线，也可以是曲线，曲线轨迹是通过构成二维平台的一维直线平台复合运动得到的。二维运动的轨迹是平面曲线，直线是其特例。根据平面坐标系的约定，把二维运动轨迹分析转化为平面坐标 xy 的平面几何曲线分析。图 1-3 所示的是一个二维平台的组成示意图，图中有一个 xy 坐标系，分别由两个独立的一维直线平台实现。


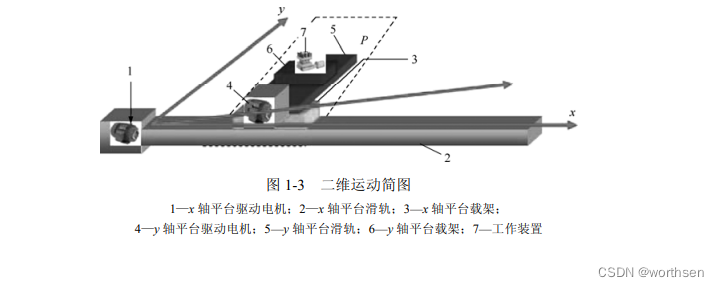
图 1-5 所示的是平面运动的另外一种形式——复合运动。

对于现实生产过程中大量应用着的取放、探针定位、物品载送等，提升其效率的有效途径之一就是复合运动。

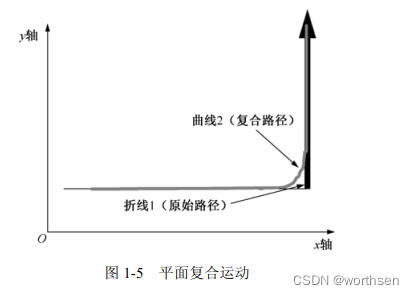
图 1-7 所示的是平面运动的轮廓线控制模式。轮廓线由一系列特征点组成，系统的运动特征是按照轮廓线运动。其方法是把轮廓的特征点存放到一组缓冲区中，并保持相关数据，然后通过这些点建立一条光滑的路径（或者称为样条曲线），该方法的优点是可以确保经过了每一个特征点。

除了把平面运动看成一个质点平面运动之外，还有一种情况就是把运动对象看成一个刚体，刚体是由一系列质点组成的。图 1-8 所示的是刚体的平面运动图。

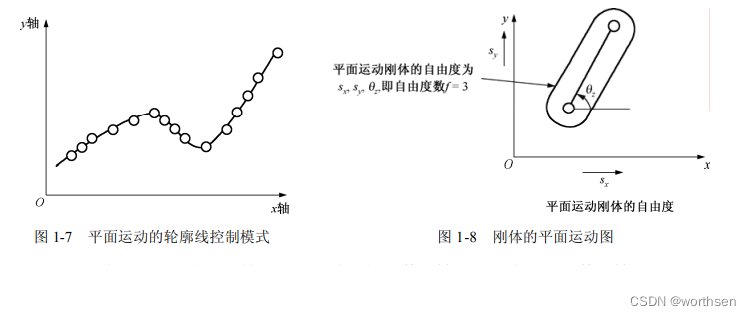
平面刚体运动可能的运动情况是：刚体能够沿着 x 轴平动，也可以沿着 y 轴平移，还可以以一个端点作为原点做旋转运动，是典型的三自由度运动。

3．三维运动
三维运动从总的运动形态可以分成两大类：三维质点运动和三维刚体运动。三维运动是二维运动的空间化，二维运动是三维运动的一个特例。三个一维运动单元的合成就是典型的三维运动，每一维度的运动形式可以是平动（位移），也可以是旋转，其运动轨迹是空间曲线。

1. 三维质点运动
   三维质点运动的移动规律与平面质点移动规律无差异，也有三类形式：第一类为空间点对点的移动，可以是直线移动，也可以是旋转运动；第二类为复合移动，是在三个运动轴按照一定的复合比例所做的运动；第三类为空间轮廓线运动。图 1-9 所示的是典型的空间质点移动矢量关系也就是从坐标原点到空间点（x0, y0, z0）的笛卡儿坐标关系。三维空间质点移动的轨迹问题还可以转化为复合移动问题和轮廓线追踪问题。

2. 三维刚体运动
   图 1-10 所示的是一个放置于三维空间坐标系内的一个刚体 A。与图 1-8 比较，图 1-10 中刚体 A 的运动要比二维平面刚体运动复杂，平面刚体如前所述只有三个自由度，而空间刚体可以沿着 x 轴平动 sx，也可以沿着 y 轴平动 sy，还可以沿着 z 轴平动 sz。刚体 A 还可以以 x 轴为轴心做旋转运动θx，类似地，也可以以 y 轴和 z 轴为轴心做旋转运动。因此，空间刚体 A 具有沿着 x、y、z 三个轴的平移自由度和三个旋转自由度. 所以空间刚体具有 6 个自由度。

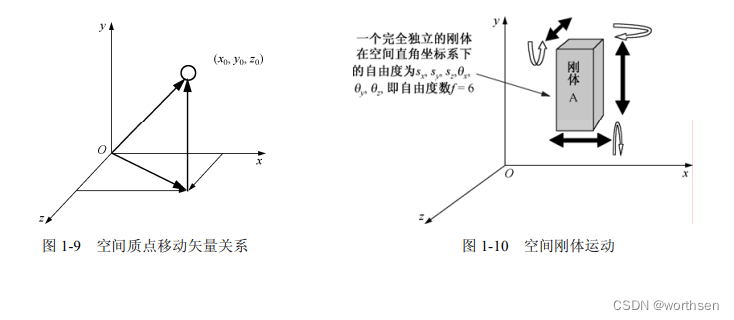
图 1-11 所示的是四个三维平台的实物。其中，图 1-11(a)是龙门架式结构三维平台，结构特点是受力均匀，这是最常见的一种应用形式；图 1-11(b)是悬臂梁式结构，往往是当空间受限时所采用的结构，很明显，这种机构的受力是不均匀的；图 1-11©是塔架式结构；图 1-11(d)是悬臂式实物图。

4．运动控制系统的轴

1. 运动轴
   通常，我们把一个定义在直线段上移动的物体或者按照预定旋转方向旋转的物体定义为运动轴。轴一般分为两类：线性轴和旋转轴。
2. 线性轴
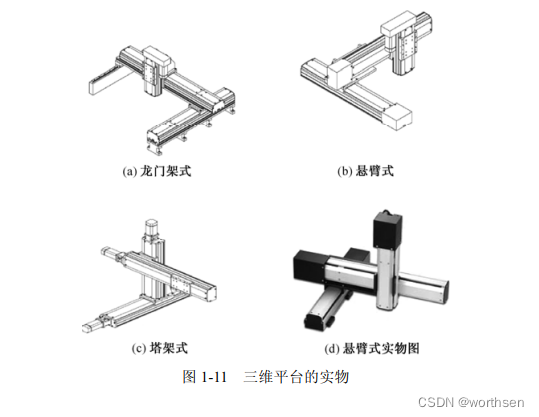
   线性轴的定义为：只有初始位置和结束位置，而且轴的当前实际位置一定是在其初始位与结束位之间，如图 1-12 所示。图 1-12 所示的是两种表现形式。图 1-12(a)是直线平移，图的左边点是起点，右边点是终点。图 1-12(b)是旋转移动，同样地，左面点是起点，右面点是终点。
3. 旋转轴
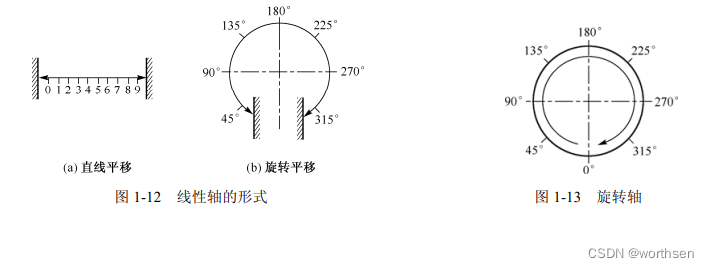
   一个周期式的旋转轴做圆周运动，其起始点是 0°，完成一个循环之后，又重新回到 0°。这种情况也称为模轴，如图 1-13 所示。
   

1.1.2 第二类运动控制问题

第二类运动控制问题与风机、水泵、压力、温度等大量实际生产、生活问题是相关联的。根据风机、水泵等的驱动特点，第二类运动控制问题都可以转化为单轴运动控制的周期式旋转控制问题。

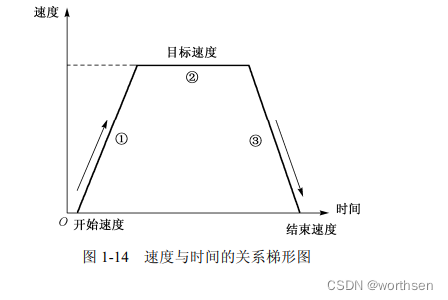
对于单轴周期式旋转控制问题，由三个要素组成：开始速度、目标速度和结束速度。图 1-14 所示的是一个速度与时间的关系梯形图，梯形由三段构成：①从开始速度位起的加速度阶段；②恒速阶段，该阶段的典型特征是速度按照目标速度运行；③减加速度阶段，该阶段将速度降到零，到达结束速度位。

1.2 运动控制系统

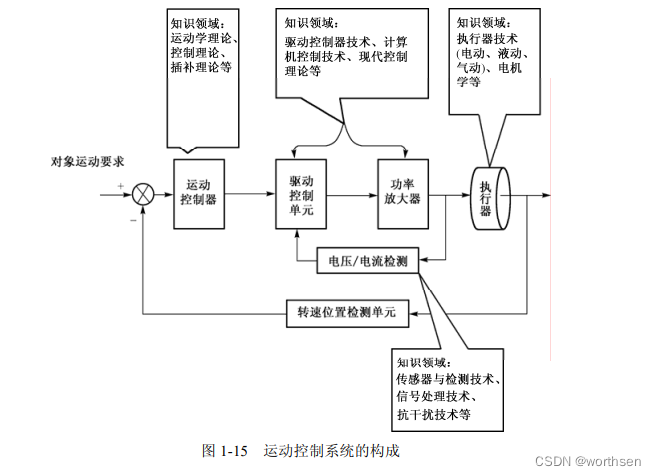
运动控制系统就是依照具体对象的运动轨迹要求，根据其负载情况，配置合理的驱动器，驱动执行电机，完成相应的运动轨迹要求的系统。典型的运动控制系统有以下部分构成：运动控制器、驱动执行器、运动反馈单元等，如图 1-15 所示。其中，运动控制器主要由三大要素构成：轨迹生成器、插补器与控制回路。

图 1-15 不仅是系统构成的反映，更是各个要素单元所涉及的知识领域的反映。其中，运动控制器的知识领域为：运动学理论、控制理论、插补理论等。驱动控制单元与功率放大器的知识领域为：驱动控制器技术、计算机控制技术、现代控制理论等。执行器的知识领域为：执行器技术（电动、液动、气动）、电机学等。转速位置检测单元与电压/电流检测的知识领域为：传感器与检测技术、信号处理技术、抗干扰技术等。

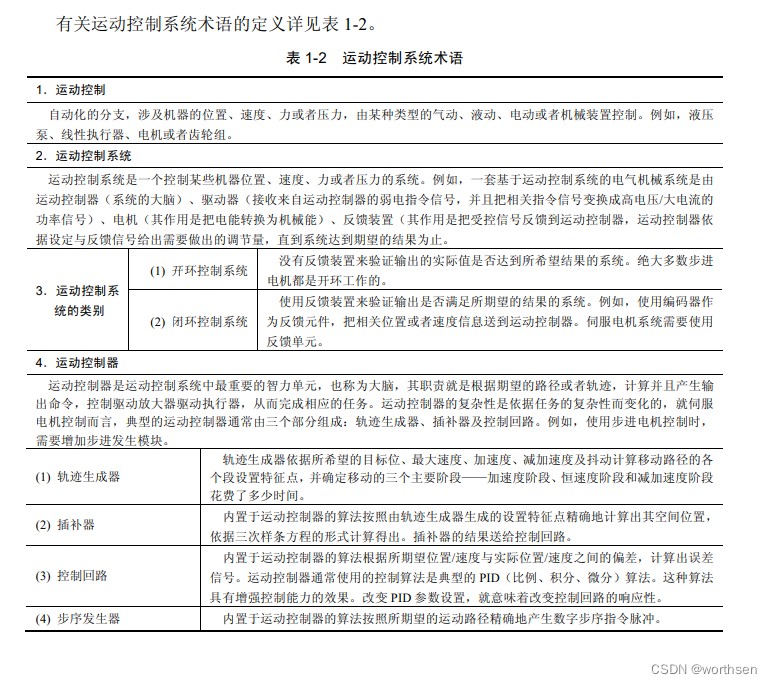
1.3 运动控制系统术语

1.4 运动控制系统的发展历程与未来发展趋势

1．运动控制与驱动技术的发展历史

发展阶段	技术分类	主要技术特征（典型代表）
最早期	模拟时代（步进时代）	步进控制器 + 步进电机 + 电液脉冲马达
20 世纪 70 年代	直流模拟时代	基于微处理器技术的控制器 + 大惯量直流电机
20 世纪 80 年代	交流模拟时代	基于微处理器的控制器 + 模拟式交流伺服系统
20 世纪 90 年代	数字化初级阶段	数字/模拟/脉冲混合控制，通用计算机控制器 + 脉冲控制式数字交流伺服系统
21 世纪至今	全数字化时代	基于 PC 的控制器 + 网络数字通信 + 数字伺服系统

2．运动控制技术目前存在的问题

1. 控制方式的问题
   (1) 脉冲信息处理与交换存在双重瓶颈，不能满足高速控制的需求。
   (2) 混合轨迹控制不能实现高精度控制。
   (3) 无协议信息交换的传递可靠性低，制约系统综合性能的提高。
   (4) 硬件规模大，影响系统可靠性的提高。
   (5) 开发、生产和使用成本高，扩展性差。

2 运动控制器技术

2.1 运动控制系统简介

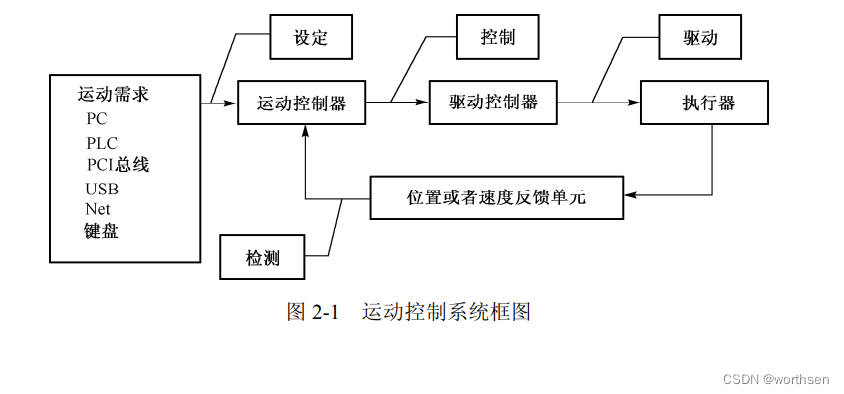
任务是具体对象对运动系统的要求，其形态可以是路径、位置增量或位移、移动速度，也可以是速度的变化率——加速度，还可以是驱动力或驱动力矩。

2.2 运动控制器的基本原理

2.2.1 运动控制器的构成

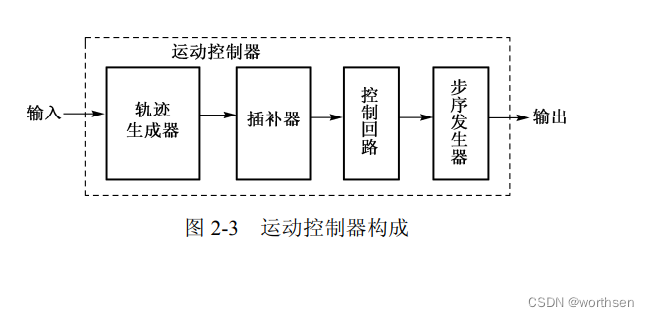
运动控制器由轨迹生成器、插补器、控制回路和步序发生器四部分构成，如图 2-3 所示。其基本原理为：运动控制器根据任务的需要，首先由轨迹生成器计算出任务希望的理想轨迹，插补器根据位置或者速度反馈单元的实际状态，按照轨迹生成器的要求，计算出驱动单元下一步将要执行的命令，然后交由控制回路进行精确控制。如果是步进电机，则还有一部分就是步序发生器，步序发生器根据控制回路控制指令进一步生成控制相序和脉冲，达到控制运动对象的目的。

2.2.2 轨迹生成器

轨迹生成器的主要作用就是根据运动任务要求，为系统生成运动轨迹，作为运动系统控制器插补器的输入设定。轨迹生成器的职责是把运动控制器的输入转化为系统希望得到的理想轨迹。运动轨迹是运动系统必须要完成的运动任务。就运动控制器而言，轨迹生成器是运动控制器三个核心部件之一，轨迹生成器性能好与坏对运动控制器起着至关重要的作用。我们这里所说的轨迹是广义上的轨迹，广义上的轨迹可以是路径或者轮廓轨迹，也可以是速度轨迹，还可以是加速度轨迹。狭义上的轨迹则特指路径或者轮廓轨迹。

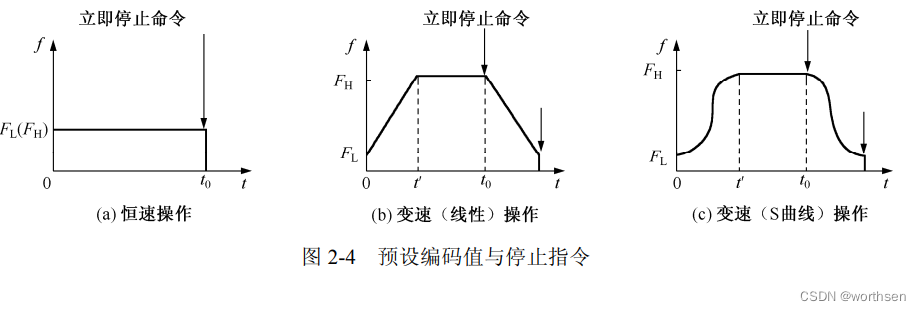
下面，通过图 2-4 说明轨迹问题。图 2-4 中有三个子图，分别表示三种停止操作过程。图中所示的速度变化曲线就是一条速度运行轨迹。由于电机的转速与供电电源频率成正比，因此尽管纵坐标表示的是频率，实质上还是电机的转速。其中，FL 表示电机最低转速值，FH表示电机最高转速值，横坐标 t 表示时间，t0 表示立即停止命令发出的时刻，即运动控制器在 t0 时刻向电机驱动单元发出停止信号。很显然，从图 2-4(a)看出，系统恒速度运行的特征是最低速度与最高速度相同，即 FL=FH，当 t≥t0 时，频率 FL(FH) = 0，表示电机转速从某一个常数值立刻下降到 0。图 2-4(b)所示的是一条典型的速度梯形曲线，电机最低速度是 FL，然后经过t′时间达到最高速度 FH，这个时段加速度是常数；在 t0时刻到来之前，系统按照 FH运行；当 t = t0时，又经过t′时段，电机转速将由 FH降低到 FL，这个时段减加速度也是一个常数。图 2-4©所示的是一条典型的速度 S 曲线，系统从 t = 0 时刻开始，初始速度是 FL，经过t′时间段，系统稳态速度变为 FH，速度的变化率是变化的，不是一个定值；当t′ ≤t < t0 时，系统速度为 FH，当 t≥t0时，系统速度由 FH变化为 FL。速度变化遵循 S 曲线。图 2-4 所示的三种操
作模式可以采用编码方式预先内置到控制器中。例如，恒速操作的编码为 001，变速（线性）操作的编码为 002，变速（S 曲线）操作的编码为 003。控制编程时，可以通过提前往控制器之中预设编码值来选择停止操作的方式。

1．点对点运动轨迹
虽然有很多种运动轨迹可以选择，但是最简单、最直接的运动曲线是点对点运动轨迹。

下面举一个简单的例子，图 2-5 所示的就是一个点对点的运动轨迹。由图可知，运动的起点从 20°开始，运动的终点到 100°结束。通常情况下，就位置或者速度系统而言，运动控制器更常用的方法是用编码器脉冲数来取代角度。点对点运动的应用范围十分宽广，包括各种大型医疗自动化诊疗设备，如 CT 机、MR 核磁共振等；机械制造业使用的各类加工中心、数控机床等；科学研究领域的自动检测与定位仪器；军事领域中的自动定位跟踪、自动瞄准系统等；民用自动设施，如电梯等（需要注意的是，自动扶梯不是点对点运动方式）。点对点运动方式的特点是运动需求描述简单，控制容易。对于点对点运动方式，负载速度从零开始，加速到设定速度，稳定运行，然后减速至停止，此时被控对象到达目标位置——终点。在一个典型的点对点运动中，速度从零开始到零结束，并启动加速和停止减速都是平滑的。

点对点运动有两种最常用的速度轨迹曲线，分别是 S 曲线和梯形曲线。点对点运动的主要研究方法是特征值描述法，其主要研究内容是运动速度轨迹特征曲线和运动加速度轨迹特征曲线。如图 2-6(a)所示，S 曲线由 7 个不同的运动时序段构成，不论是速度曲线还是加速度曲线均有 7 个时序段。对于这 7 个时序段，时序段Ⅰ中运动对象从静止开始运动，速度平滑增加，而加速度则线性增加，直到最大加速度；时序段Ⅱ中运动对象的速度是线性增加，而加速度则维持在最大加速度，直到时序段Ⅱ结束；时序段Ⅲ中速度继续圆滑上升至最高速度，加速度则呈线性下降，直至加速度为零；时序段Ⅳ中速度保持恒定，直至时序段Ⅳ结束，此时速度达到最大值，加速度则为零。时序段Ⅴ、Ⅵ、Ⅶ是减速方式，它们与时序段Ⅰ、Ⅱ、Ⅲ的加速方式完全是对称的。

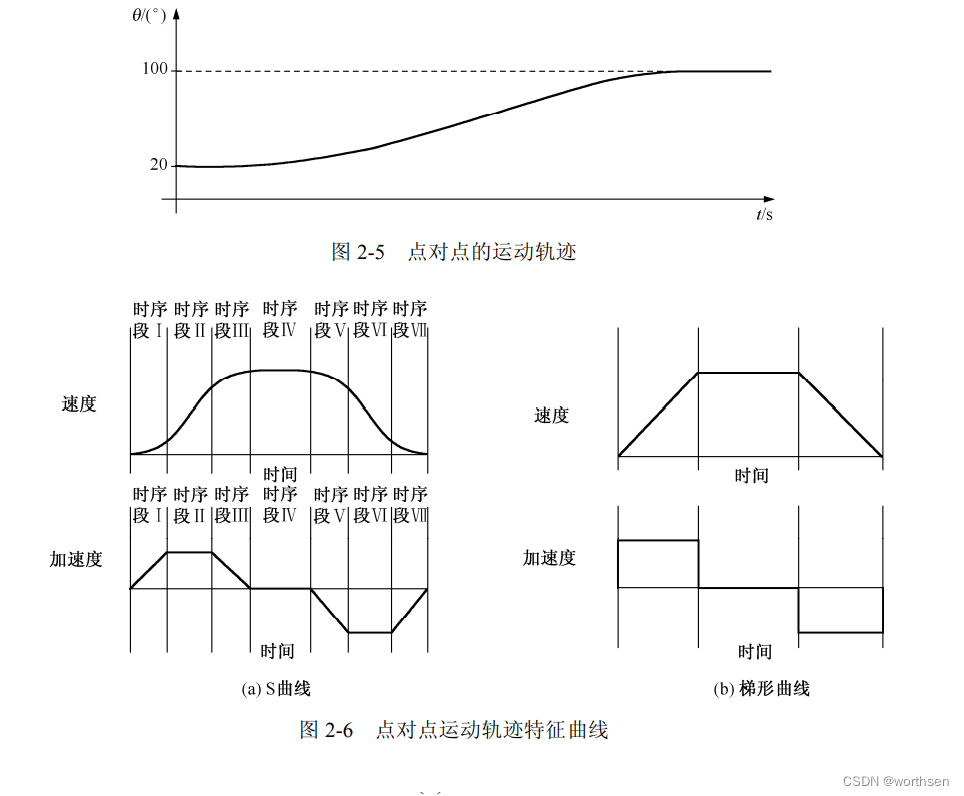
梯形曲线由三个时序段构成，如图 2-6(b)所示。很显然，梯形曲线是 S 曲线的一个子集，与 S 曲线相比，它仅具有时序段Ⅱ（恒加速）、时序段Ⅳ（恒速）和时序段Ⅵ（恒减速）三个时序段。

S 曲线与梯形曲线进行对比，可以看出 S 曲线的速度曲线的平滑性远远优于梯形曲线的速度曲线；同时，也发现 S 曲线的加速度曲线是连续的，而梯形曲线的加速度曲线是阶跃函数，存在突变点，这表明前者的平稳性大大优于后者。因此，对于需要高的运动平稳性的场合，可以优先选用 S 曲线。

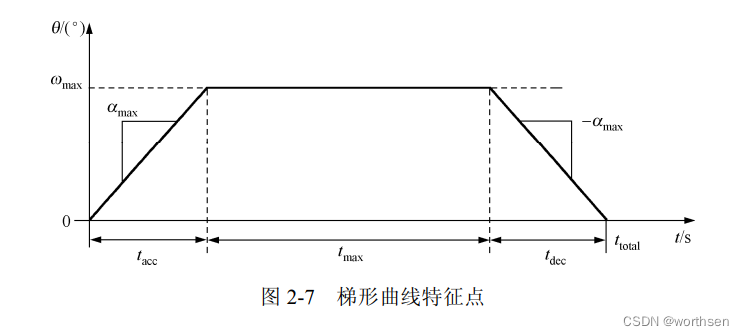
图 2-7 所示的是梯形曲线的特征点，其中 ${\omega }_{max}$ 为最大速度，${\alpha }_{max}$ 为最大加速度，$t_{acc}$ 为加速度时间，$t_{dec}$ 为减速度时间，$t_{max}$ 为最大速度时间，$t_{total}$ 为整个运动时间，则有如下公式。
$$t_{acc}=t_{dec}=\frac{{\omega }_{max}}{{\alpha }_{max}}\text{\hspace{1em}(2-1)}$$
$$t_{total}=t_{acc}+t_{max}+t_{dec}\text{\hspace{1em}(2-2)}$$
$$\theta =\frac{1}{2}{t}_{acc}{\omega }_{max}+t_{max}{\omega }_{max}+\frac{1}{2}{t}_{dec}{\omega }_{max}={\omega }_{max}(\frac{t_{acc}}{2}+t_{max}+\frac{t_{dec}}{2})\text{\hspace{1em}(2-3)}$$
$$t_{max}=\frac{|\theta |}{{\omega }_{max}}-\frac{t_{acc}}{2}-\frac{t_{dec}}{2}\text{\hspace{1em}(2-4)}$$
注意，如果由式(2-4)计算出的时间是负值，那么说明实际速度不可能达到最大速度，而且速度曲线不是一个梯形，而是一个三角形。式(2-1)～式(2-4)是梯形速度曲线特征点的基本关系式。

梯形曲线的缺陷是如果加速度和减速度是定值，那么在加速度段和减速度段，负载会发生抖动。在某些场合，这种抖动希望能减小到最小，故多项式曲线就起到这样的作用。图 2-9所示的是一种典型的多项式曲线。由图可见，在加速度段和减加速度段，速度由多项式 $\omega (t)=A{t}^2+Bt+C$ 表示。这种多项式曲线的最大特色为速度平滑，稳定性好，不存在负载抖动的问题。

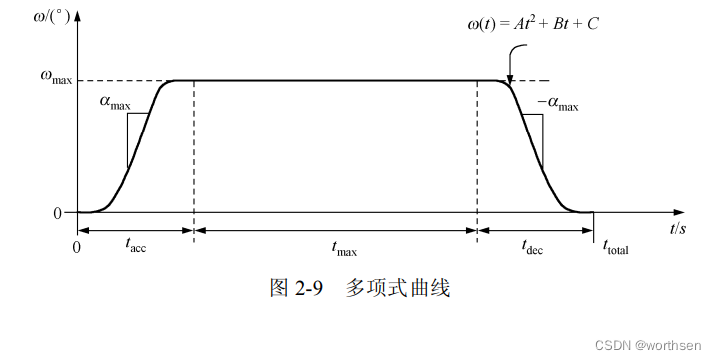
对于图 2-9 所示的多项式曲线，已知四个参数值 ${\theta }_{start}、{\theta }_{end}、{\omega }_{max}、{\alpha }_{max}，$即起点位置、结束位置、最大角速度与最大角加速度，并且如图 2-9 所示的速度多项式的约束条件是
$$\begin{array}{rl}\omega (0)& =0\\ \omega (\frac{t_{acc}}{2})& =\frac{{\omega }_{max}}{2}\\ \frac{d}{dt}\omega (0)& =0\\ \frac{d}{dt}\omega (\frac{t_{acc}}{2})& ={\alpha }_{max}\end{array}$$
因此，按照上述约束条件，可以计算出多项式的系数 A、B 和 C。
$$\begin{array}{rl}0=A\cdot 0^2+B\cdot 0+C& \Rightarrow C=0\\ 0=2A\cdot 0+B& \Rightarrow B=0\\ {\omega }_{max}=A{t}_{acc}^2& \Rightarrow A=\frac{{\omega }_{max}}{t_{acc}^2}\end{array}$$
故
$$\begin{array}{rl}A& =\frac{{\omega }_{max}}{t_{acc}^2}=\frac{{\alpha }_{max}}{2t_{acc}}\\ t_{acc}& =\frac{2{\omega }_{max}}{{\alpha }_{max}}\end{array}$$
则
$$A=\frac{{\alpha }_{max}}{2t_{acc}}=\frac{{\alpha }_{max}}{2(\frac{2{\omega }_{max}}{{\alpha }_{max}})}=\frac{{\alpha }_{max}^2}{4{\omega }_{max}}$$
那么，可以求得图 2-9 中所描述的第一段曲线的方程为
$$\omega (t)=\frac{{\alpha }_{max}^2}{4{\omega }_{max}}{t}^{2}0\le t<\frac{t_{acc}}{2}\text{\hspace{1em}(2-9)}$$
同理，第二段曲线的方程为
$$\begin{array}{rl}\omega (t)& ={\omega }_{max}-\frac{{\alpha }_{max}^2}{4{\omega }_{max}}(t_{acc}-t{)}^2\\ \omega (t)& ={\omega }_{max}-\frac{{\alpha }_{max}^2}{4{\omega }_{max}}(t^2-2t_{acc}t+t_{acc}^2)\frac{t_{acc}}{2}\le t<t_{acc}\end{array}\text{\hspace{1em}(2-10)}$$
第一段曲线（加速段）的路程为
$$\begin{array}{rl}{\theta }_{acc}& ={\int }_0^{\frac{t_{acc}}{2}}\frac{{\alpha }_{max}^2}{4{\omega }_{max}}{t}^{2}dt+{\int }_{\frac{t_{acc}}{2}}^{t_{acc}}({\omega }_{max}-\frac{{\alpha }_{max}^2}{4{\omega }_{max}}(t^2-2t_{acc}t+t_{acc}^2))dt\\ & =\frac{{\alpha }_{max}^2}{12{\omega }_{max}}{t}^3{|}_0^{\frac{t_{acc}}{2}}+({\omega }_{max}t-\frac{{\alpha }_{max}^2}{4{\omega }_{max}}(\frac{t^3}{3}-t_{acc}{t}^2+t_{acc}^{2}t)){|}_{\frac{t_{acc}}{2}}^{t_{acc}}\\ & =\frac{{\alpha }_{max}^2}{12{\omega }_{max}}\frac{t_{acc}^3}{8}+{\omega }_{max}{t}_{acc}-\frac{{\alpha }_{max}^2}{4{\omega }_{max}}(\frac{t_{acc}^3}{3}-t_{acc}^3+t_{acc}^3)-{\omega }_{max}\frac{t_{acc}}{2}+\frac{{\alpha }_{max}^2}{4{\omega }_{max}}(\frac{t_{acc}^3}{24}-\frac{t_{acc}^3}{4}+\frac{t_{acc}^3}{2})\\ & =\frac{{\alpha }_{max}^2}{96{\omega }_{max}}{t}_{acc}^3+\frac{{\omega }_{max}^2{t}_{acc}}{2}-\frac{{\alpha }_{max}^2}{12{\omega }_{max}}{t}_{acc}^3-\frac{7{\alpha }^{2}max}{96{\omega }_{max}}{t}_{acc}^3\\ & =\frac{-14{\alpha }_{max}^2}{96{\omega }_{max}}{t}^3+\frac{{\omega }_{max}{t}_{acc}}{2}\end{array}\text{\hspace{1em}(2-11)}$$
第二段曲线（最大速度）的时间为
$$t_{max}=\frac{(\theta -2{\theta }_{acc})}{{\omega }_{max}}\text{\hspace{1em}(2-12)}$$

2．路径轨迹
沿着一条路径的所有位置点来描述的轨迹曲线就是路径轨迹曲线。路径轨迹曲线还有其他说法，如位置轨迹曲线和轮廓轨迹曲线，都是表述行走的路径，但是路径与轮廓还是有所差别，路径更强调的是行驶线路，而轮廓则更加强调走过的具体位置及其精度。那么，什么样的场合适合于采用路径轨迹曲线呢？通常，当运动需求没有速度或者加速度要求、而对路径或者形状有很严格的要求时，采用这种方法。路径轨迹曲线的运动表述法利用的是参数函数“p(u)”。当参数值 u 的值域是 0～1 时，函数值的变化范围也是 0～1。无论如何，函数的参数选择条件是，运动开始与停止时的速度都是 0，这样就使得最终多项式方程简化为公式(2-11)。随后这个方程可以用在式(2-9)中，使控制器能够在起点和终点之间产生一条光滑的运动路径。
$$\theta (t)={\theta }_{start}+({\theta }_{end}-{\theta }_{start})p(\frac{t-t_{start}}{t_{end}-t_{start}})\text{\hspace{1em}(2-13)}$$
式中，${\theta }_{start}$ 为运动的起点位置，${\theta }_{end}$ 为运动的结束位置， $t_{start}$ 为运动的开始时间， $t_{end}$ 为运动的结束时间。
$$p(u)=A{u}^3+B{u}^2+Cu+D\text{\hspace{1em}(2-14)}$$
式中，多项式的系数是
$$\begin{array}{rl}p(0)& =0\\ p(1)& =1\\ \frac{d}{d\tau }p(0)& =0\\ \frac{d}{d\tau }p(1)& =0\end{array}$$
然后，按照下列计算式计算求出，即
$$\begin{array}{rl}p(0)& =0\Rightarrow 0=A\cdot 0^3+B\cdot 0^2+C\cdot 0+D\\ p(1)& =1\Rightarrow 1=A\cdot 1^3+B\cdot 1^2+C\cdot 1+D\\ \frac{d}{d\tau }p(0)& =0\Rightarrow 0=3\cdot A\cdot 0^2+2\cdot B\cdot 0+C\\ \frac{d}{d\tau }p(1)& =0\Rightarrow 0=3\cdot A\cdot 1^2+2\cdot B\cdot 1+C\\ B& =(-\frac{3}{2})A\\ A=-2,B& =3,C=0,D=0\\ p(u)& =-2u^3+3u^2\end{array}\text{\hspace{1em}(2-15)}$$

3．多轴运动轨迹
除了单轴运动之外，很多机器的运动轨迹都是多轴运动复合的产物。例如，一个机器人完成平面运动，从一个位置点到达另一个新的位置点，必须完成两点之间的复合运动。

在机械加工领域，工作装置头的运动往往是一种多轴运动。对于平面二维复合运动，有办公室里广泛使用的打印机、绘图仪，机械加工领域中的车床、排钻等；对于空间三维点位运动，有机械加工中的数控钻、数控坐标镗、数控坐标铣、加工中心与柔性制造系统，大型物流中心中的自动运搬机、行车等。

4．往复运动轨迹
除了点对点运动之外，还有一个范围广泛的应用就是往复运动。往复运动的运动轨迹是周期的，其特点是由一个主定时器或编码器做运动索引。电子凸轮也属于运动索引范畴，它还有一个功能就是变速器，其变速功能是通过电子齿轮实现的。

电子凸轮（也称电子轴）的设定方式有两种：①输入特征参数，②使用可下载表格（这种方式基本上是通过串口或者数据总线完成的）。表格的数据用来为主编码器或者主时钟提供基本数据，每一项表格数据对应编码器的一个位置，每一个编码器位置确定对应的一个运动目标点。可以提前把各类运动轨迹编制成数据表，用户根据实际需要下载一个梯形曲线或一个 S 形曲线。更常见的是，还可以自定义一个配置文件，模拟一个专门的机械凸轮的功能。

有很多方法可以指定主时钟和控制轴之间的关系。最常见的方法是使用编码器计数的数值换算对应主编码器旋转的角度。例如，用主编码器旋转 360°对应编码器计数数值变化，并允许在表的每个位置定义一个或多个输出点，当执行表时，在阅读表的最后一个位置的数据之后，运动控制器将对表格数据进行覆盖，并重新从起点开始，因此开始和结束位置的目标必须是相同的，这样才能避免产生跳跃运动。

2.2.3 插补器

1．插补器定义
插补器是运动控制器中的算法。所谓“插补”，就是在一条已知起点和终点的曲线上进行数据点的密化。通常，可以采用的形式有简单的一次插补、二次插补或者更为复杂一些的三次样条函数插补。插补结果将送入控制回路。

由插补的定义可以看出，在轮廓控制系统中，插补是最重要的功能，是轮廓控制系统的本质特征。插补算法的稳定性和精度将直接影响到 CNC 系统的性能指标，所以为使高级数控系统能发挥其功能，不论是在国外还是国内，精度高、速度快的插补算法一直是科研人员希望能够突破的难点，也是各数控公司保密的核心技术。例如，西门子、Fanuc 公司的数控系统，其许多功能都是对用户开放的，但其插补算法却从不对用户开放。

2．插补的种类
插补的种类很多。按插补工作是由硬件电路还是由软件程序完成的，可将其分为硬件插补和软件插补。图 2-11 所示的就是直线插补和圆弧插补，以及二者的组合。

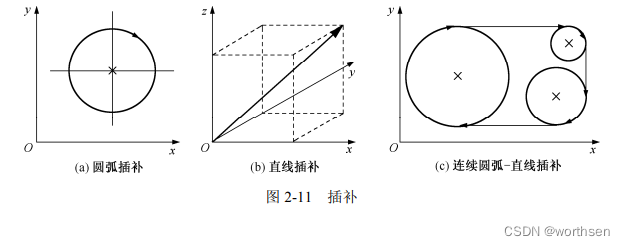
按照数学模型，可分为一次（直线插补）、二次（圆弧插补、抛物线插补、椭圆、双曲线、二次样条曲线）和高次（样条线插补）。

目前，应用最多的插补分为两类：基准脉冲插补和数据采样插补。下面对插补做一下详细的分析。

1. 直线插补
   (1) 直线插补原理
   若坐标点 0 0 (, ) x y 和 1 1 (, ) x y 已知，则直线插补就是这两点之间的直线。对于 x∈ 0 1 (,) x x ，符合直线规则的 y 值可以由下式求出：
   $$\frac{y-y_0}{x-x_0}=\frac{y_1-y_0}{x_1-x_0}\text{\hspace{1em}(2-16)}$$
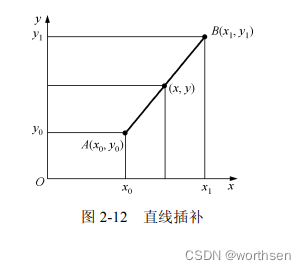
   如图 2-12 所示， 0 0 A(, ) x y 和 1 1 Bx y (, ) 是已知点，直线 AB上点 (, ) x y 是两个点间的直线插值，直线插补依据 x，就能求得 y，即
   $$y=y_0+(x-x_0)\frac{y_1-y_0}{x_1-x_0}=y_0+\frac{(x-x_0)y_1-(x-x_0)y_0}{x_1-x_0}\text{\hspace{1em}(2-17)}$$
   式(2-17)还可以被看成加权平均数，加权值大小反比于终点与未知点间的距离。距离越近，影响越大。权值是 $\frac{x-x_0}{x_1-x_0}$ 和 $\frac{x_1-x}{x_1-x_0}$ 。
   在这个区间之外，计算采用的是与式(2-17)形式相同的线性归纳法。

在计算机图形学中会经常应用到直线插补。两个值间的直线插补是基本的操作，常用单词“lerp”作为计算机图形学领域中的术语，“lerp”的确切含义就是直线插补。

(2) 直线插补步骤
直线插补一般有三个步骤：①偏差函数的构造，②偏差函数递推计算，③终点判别。

2) 圆弧插补
(1) 圆弧插补原理
圆弧插补算法针对的是多轴运动，其思想就是用弦进给代替弧进给。圆弧插补分为顺时针圆弧插
补和逆时针圆弧插补两种。对于机械加工而言，当加工圆弧时，可以将加工点到圆心的距离与该圆的
半径相比较，以此来反映加工时的偏差。以第一象限逆圆弧为例，可推导出圆弧插补的偏差计算公式。

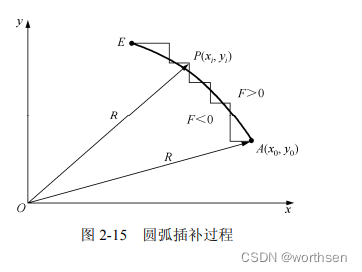
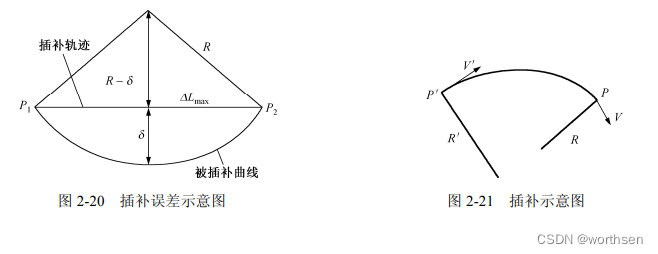
要加工如图 2-15 所示的圆弧 AE。圆弧 AE 位于第一象限，逆时针走向，半径为 R，以原点为圆心，
起点坐标为 $A(x_0,y_0)$，对于圆弧上任一加工点的坐标设 为 $P(x_i,y_i)$ 。 点 P 与圆心的距离的平方为 $R_p^2=x_i^2+y_i^2$。

运用上述法则，使用偏差公式，便可加工出图 2-15 所示折线的近似圆弧。
(2) 圆弧插补步骤
圆弧插补的具体步骤与直线插补完全相同，也是三个步骤：①偏差函数的构造，②偏差函数递推计算，③终点判别。

3) 抛物线插补
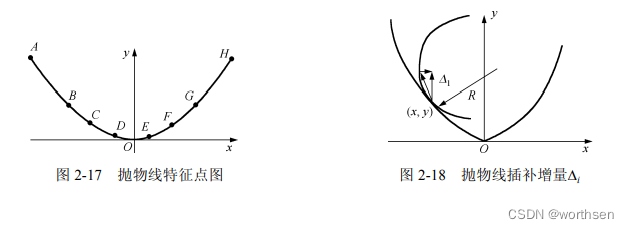
抛物线插补算法是一种新型插补算法。抛物线函数是一种简单函数，既可以利用硬件，也可以利用软件来实现。

抛物线插补算法以抛物线顶点的坐标值作为原点，抛物线的起点和终点都换算成以抛物线顶点为原点的相对坐标。抛物线的开口方向不同，它的数学表达式也不一样。为简明起见，以一种情况为例说明抛物线插补计算的方法和过程。设抛物线方程为
$$x^2=2py\text{\hspace{1em}(2-29)}$$

4. 样条插补
   为了满足快速成形制造及模具加工领域中高速度和高精度的要求，利用 B 样条曲线良好的局部控制性和计算机 CPU 处理速度快的优点，开发出基于三次非均匀 B 样条曲线的插补算法。
   (1) 样条插补原理
   快速成形制造系统读入 STL 文件后，首先利用拟合算法将这些离散的数据点拟合为分段的三次非均匀无理 B 样条；然后构造一链表用来保存每段 B 样条的系数和长度；插补时读入此链表，根据分段标志，以当前插补点为控制目标，求出下一插补点的坐标值，完成变速度自适应插补。
   (2) 样条插补步骤
   样条插补算法采用参数化数据采样原理来实现插补过程，其基本思想是按照给定的采样周期将时间轴分成非均匀间隔的小区间，插补过程中根据给的速度、加减速要求和允许误差，在各采样周期产生空间小直线段 $\Delta L_1、\Delta L_2、\Delta L_3、...、\Delta L_m"$ ，… 去逼近被插补曲线，逐步求得伺服控制所需的各插补直线段端点 $p_1、p_2、p_3、...、p_m、...$ 的坐标值，即以当前插补点的速度为控制目标，以插补周期 $\tau$ 内的插补步长等于曲线上的弧长为依据，最终求出下一插补点的坐标。
   (3) 样条插补计算

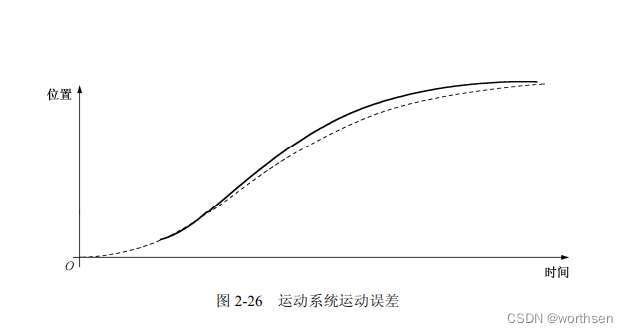
图 2-26 所示的是理论期望的位置与实际得到的位置误差关系图，其中实线是期望的位置，虚线是实际得到的位置。

2.2.4 控制回路

在运动控制器中固化有控制算法，由算法依据期望的位置或速度与实际的位置或速度的差值信号进行计算。运动控制器通常使用增强型 PID（比例、积分、微分）算法，使得控制功能更加强大。PID 的增益设定值决定控制回路的控制能力。下面结合前馈控制研究实际运动控制系统控制回路的基本架构，如图 2-27 所示。图中包括两个组成部分：一是实时控制回路，二是物理系统。这里所说的物理系统就是执行器，具体在本系统中是电机。图 2-27 中 ${\theta }_d$是位置输入设定；${\theta }_a$ 是位置实际输出，实时控制回路的作用是为物理系统提供控制指令；${\omega }_d$是前馈控制输入设定值，通过 ${\omega }_d$ 的变更，就可以实现对算法的修正。

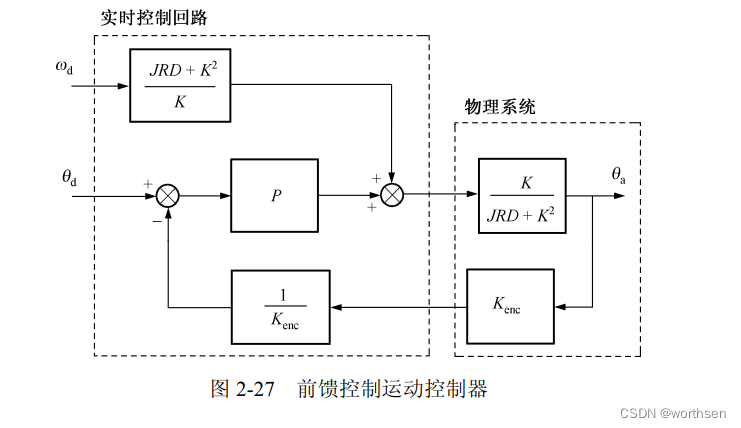
图 2-28 所示的是多回路运动控制器的组合控制回路。该系统具有灵活的组合性，可以实现单回路（位置、速度、力矩）控制，也可以实现双回路控制，还可以实现三回路控制。其基本控制程序也是三种调节器的控制算法（位置、速度、力矩），已经固化在只读存储器中。用户与运动控制器的通信可以通过 CAN、RS232、RS485 来实现。系统中还有八路 I/O 控制接口，其中六路输入、两路输出，具体如图 2-28 所示。

随着智能控制技术的发展，新型运动控制系统控制回路开始采用模糊 PID 算法。下面举一个实例。

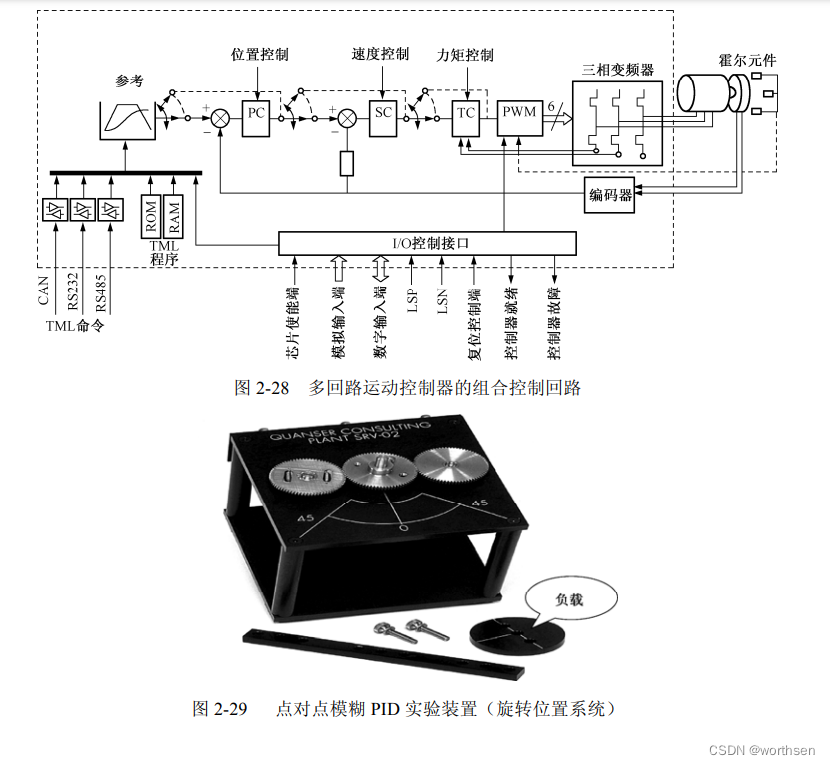
图 2-29 所示的是一个实验装置，任务就是实现点对点的运动。它由一套伺服电机驱动器、伺服电机、编码器和 PC 组成。控制器是 PC，PC 上运行的控制软件是利用 MATLAB 的实验程序。

1．数学模型
忽略系统的非线性，按照牛顿学有关定律，这套旋转位置系统实验装置的动态数学模型为
$$\frac{{\theta }_1(s)}{V_m(s)}=\frac{64.12}{s(s+36.43)}\text{\hspace{1em}(2-45)}$$

图 2-30 所示的是一个模糊 PID 调节器的系统框图，其基础算法是 PID 算法，但 P、I、D参数$（K_P、K_I、K_D）$是依据输入与输出的误差及误差的变化率来决定的。

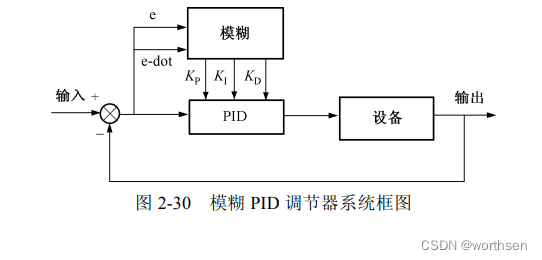
2．PID 标称值设计
图 2-30 所示的 PID 调节器的控制算法可以用式(2-33)表示。$K_P、K_I、K_D$ 分别为调节器增益的比例、积分和微分。
$$e(t)=K_{p}e(t)+K_i{\int }_0^{t}e(t)dt+K_d\frac{de(t)}{dt}\text{\hspace{1em}(2-46)}$$

2.3 运动控制器的硬件

1. 基于微处理器（MCU）的技术
   8位、16位、32位单片机。
   

2. 基于专用集成电路的技术
   利用一块专用芯片 Application Specific Integrated Circuit（ASIC）可以实现某些特定的控制算法如 PID 算法、编码器信号处理等功能。用户可以通过发送专用指令的方式对其进行控制。此类技术的优点是使用相对容易，系统输入/输出指令跟随性强、响应快速、可靠性高。NPM 公司的 PCL6045B、NOVA 公司的 MCX314 等就是专用运动控制芯片。这类控制器的不足之处在于不易升级，控制算法变更升级不易，硬件成本价格高。

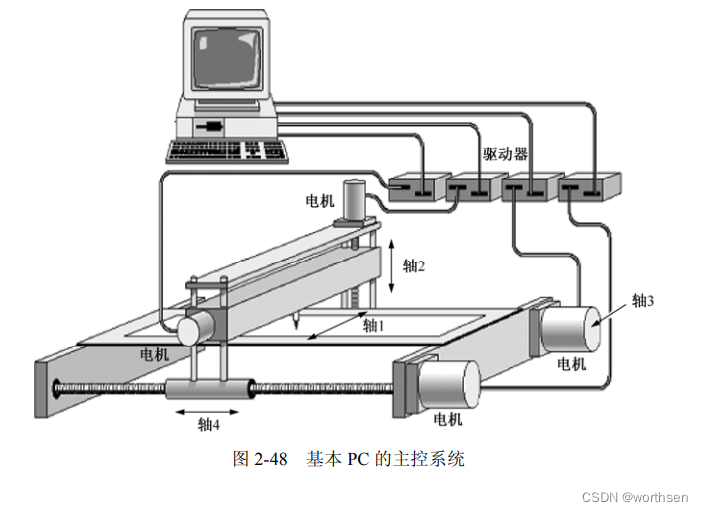
3. 基于 PC 的技术
   由于 PC 发展迅速，技术成熟，软件资源丰富，因此充分利用 PC 资源，并将其功能集成到运动控制器中，已成为世界各国发展研究的重点。具体地说，PC NC 就是在 PC 硬件平台和操作系统的基础上，利用公共软件和硬件板卡，按照运动控制器的要求，构造出运动控制系统。由于 PC 总线是一种开放性的总线，PC 系统的硬件体系结构具有开放性、模块化、可嵌入的特点，为广大用户通过开发应用软件给数控系统追加功能和实现功能个性化提供了保证。PC 的运动控制器的缺点是与专用运动控制系统相比实时性差，可靠性也不如专用运动控制系统高，对实际编程者的水平要求较高，尤其是要利用 PC 进行高性能运动控制算法开发，经验变得十分重要，而且验证平台本身的成本也不低，故基于 PC 的运动控制器系统比较适合于中高档、多用途的运动系统对象。
   

4. 基于 DSP 的技术
   20 世纪 90 年代以来，随着微电子技术水平的快速提升，数字信号处理（DSP）芯片因其高速运算能力而被越来越广泛地用于运动控制系统中。DSP 芯片使复杂算法的实时性得到有效保证，因此 DSP 在运动控制器中得以应用。目前，主流的运动控制器都采用 DSP 技术。比如，美国 Delta 公司的 PMAC 运动控制卡采用了 Motorola 公司的 DSP56001；国内固高科技有限公司的 GT—400 运动控制卡采用了 ADI 公司的 ADSP2181。

5. 基于可编程逻辑控制器的技术
   在可编程逻辑控制器上实现运动控制器的算法和电路，可以提高系统的集成度和性能，具有很大的灵活性。但整个系统需要大量的逻辑单元，编程难度大，价格昂贵。所以，这种方式的实现也只有在一些功能较简单、快速性要求较高的场合。

6. 基于多核处理器的技术
   此类控制器在一个芯片内部集成了多个处理器内核。如 TI 公司的达·芬奇平台集成了一个DSP C64X 内核和一个 ARM9 内核，其中 DSP 用于运算，ARM 用于控制。多核处理器技术是未来处理器发展的一个方向。

运动控制器的数据传递形式可分为总线式和网络式。运动控制器的总线式有 ISA、PCI、VME、USB、SPI、STD 总线、CAN 总线；网络式有 Motionnet、Ethernet、Internet 等。

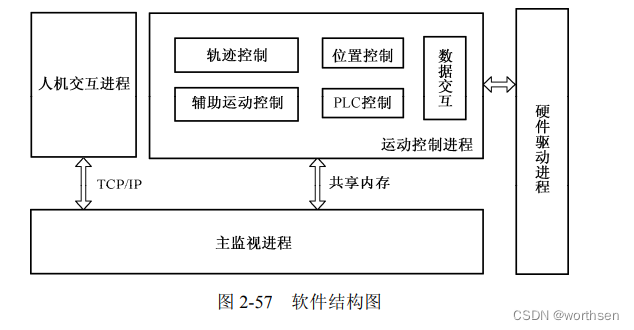
2.4 运动控制器的软件

运动控制系统总体来说是一个复杂的控制系统，兼有控制实时性、功能多样性、性能层次性和界面个性的要求。如何构建功能模块，实现功能模块的有机组合，达到实时性和非实时性的有机统一，是采用所谓引擎机制实现具体运动控制器产品的决定性技术。其实质是采用特定的方法完成软件的二次组装并实现可靠高效的信息交互。软件可以采用的支撑技术有参数定制技术、软件组装技术、进程通信技术和脚本技术等。运动控制器软件系统可以简单地划分为界面、运动控制和伺服驱动三大部分。

3 执行器技术

执行器在运动控制系统中是必不可少的元件，是现实系统完成运动任务的关键。随着现代科技的快速发展，执行器技术也得到了长足的进步。

1．执行器的分类
执行器种类繁多、大小各异，但可以按照其动力来源等特点加以区分。
(1) 按照动力来源，执行器可分为电动执行器、液压执行器、气动执行器和新型微机电执行器。
(2) 按照运动部件结构特征，执行器可分为缸类执行器、马达类执行器等。
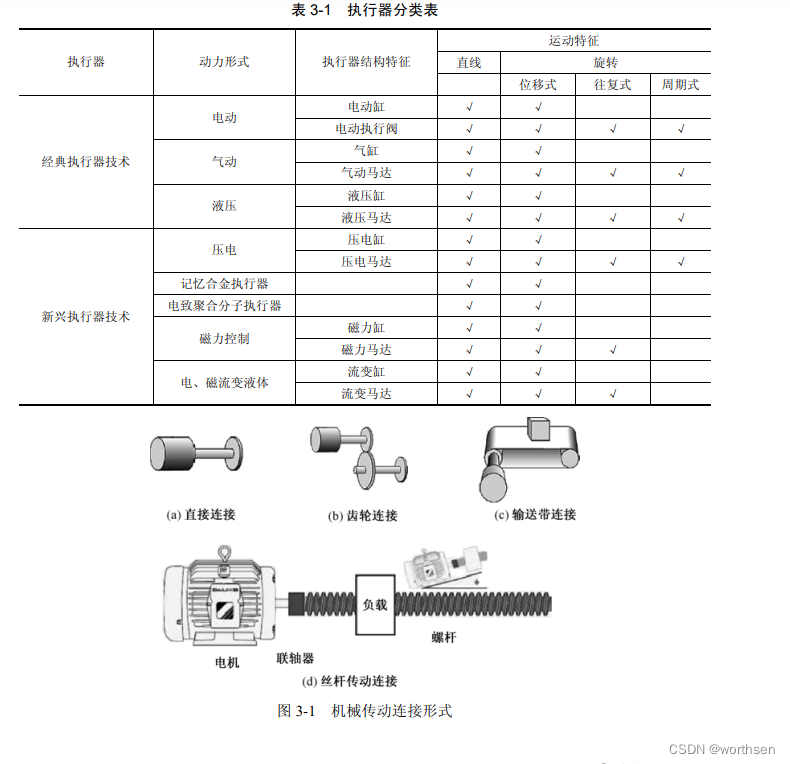
(3) 按照运动轨迹特征，执行器可分为直线型执行器、旋转型执行器，旋转型执行器又可分为位移式、周期式和往复式。
(4) 对于新型执行器，有压电执行器，记忆合金执行器，电致聚合分子执行器，磁力控制执行器，电、磁流变液体执行器等。

2．执行器的设计
执行器的设计是建立在系统运动功能分析的基础上的。要完成执行器设计，首先需要明确运动控制系统所要完成的机械任务，建立对系统的机械分析，主要包括运动学分析与力学分析。

通过对基本机械连接方式的分析，可计算出机械传动机构的惯性矩。这类系统可分为四种基本连接形式：直接连接、齿轮连接、输送带连接和丝杆传动连接，如图 3-1 所示。

4 直流电机控制技术

4.1 直流电机调速概述

4.1.1 直流电机调速的发展历程

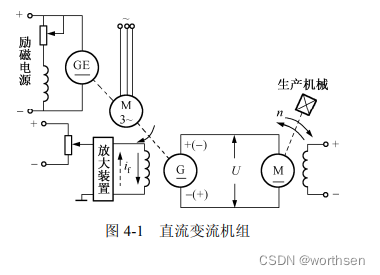
1．变流机组时代
图 4-1 所示的是早期直流电机的调速方案，称为直流变流机组。系统主要由 5 大部件组成：原动机、直流发电机、直流电动机、励磁电源和生产机械。其基本工作原理是：一台三相交流电动机拖动一台直流发电机，直流发电机发出直流电，作为直流电动机的供电电源，然后直流电动机拖动生产机械。通过对励磁电路和放大装置的控制，就能改变直流发电机的输出电压，从而达到控制直流电动机转速的目的。

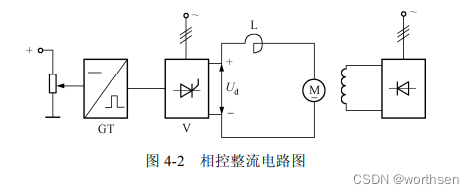
2．相控整流时代
20 世纪 50 年代末期，随着电力电子技术的早期代表——晶闸管（SCR）的出现，直流电机调压调速技术进入到一个新的时期。图 4-2 所示的是相控整流电路图。相控整流由 5 大部件组成：相控整流器、电抗器、直流电机、直流励磁控制电路和相控整流器触发电路。其工作原理是：相控整流触发电路根据设定对相控整流器进行控制，输出电压可调的直流电，经电抗器后供给直流电机。当需要改变直流电机转速时，只要改变触发电路的触发角，就可实现调速的目的。但是由于晶闸管属于半控型器件，其最大问题就是会对电网造成纹波干扰。因此，这项技术在 20 世纪 80 年代后期就逐渐被淘汰了。

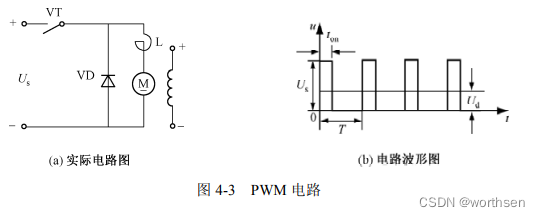
3．PWM 变频技术时代
随着电力电子技术的快速发展，自关断器件（MOSFET、IBGB、GTR、GTO）的开关频率大大提高。与相控整流器相比，PWM 变换器直流调速系统具有较高的动态性能和较宽的调速范围，其综合性能明显优于相控方式，主要优点有：
(1) 主电路结构简单，所需功率器件少；
(2) 电枢电流连续性好，谐波少，电机的损耗和发热小；
(3) 低速性能得到改善，稳速精度提高，因而调速范围增大；
(4) 系统的频带宽，快速性能好，动态抗干扰能力增强；
(5) 主电路元件工作在开关状态，导通损耗小；
(6) 直流电源采用三相可控整流，电网的功率因数提高。

由于 PWM 调压调速的优点较其他直流调速方法更加合理，因此目前 PWM 直流调速已经成为核心技术。

图 4-3 所示的就是一个典型的 PWM 电路。

4.1.2 直流电机的调速方法

1．改变电枢回路电阻调速法
2．减弱磁通调速法
3．调节电枢电压调速法

4.1.4 直流 H 型可逆 PWM 变换器-电机系统的能量回馈

如图 4-14 所示，直流 H 型可逆 PWM 变换器-电机系统由一个三相整流桥组件、一个蓄能平波电容器、一套 H 型可逆 PWM 变换电路组件和一台直流电机组成。直流电机采用他励式供电方式，其电路功能如下。
(1) 由 6 个二极管组成的整流器把电网提供的交流电整流成直流电。
(2) 直流电源采用大电容滤波。
(3) PWM 组件对电机电枢电压进行控制。

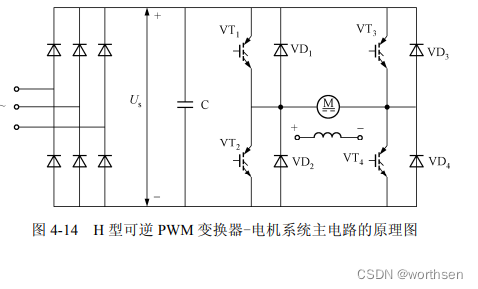
图 4-14 所示的电路存在如下问题。
1．电能回馈问题
(1) 当电机工作在回馈制动状态时，将动能转变为电能并回馈到直流侧。
(2) 由于二极管整流器的能量单向传递性，电能不可能通过整流装置送回交流电网，只能向滤波电容器充电。
(3) 由此产生了电能回馈问题。
2．泵升电压
(1) 对滤波电容器充电的结果会造成直流侧电压升高，称为“泵升电压”。
(2) 系统在制动时释放的动能将表现为电容器储能的增高，所以要适当地选择电容器的电容量或采取其他措施，以保护电力电子功率开关器件不被泵升电压击穿。储能的增量约等于电机系统在制动时释放的全部动能。

4.1.5 直流 PWM 调速系统的数学模型及机械特性

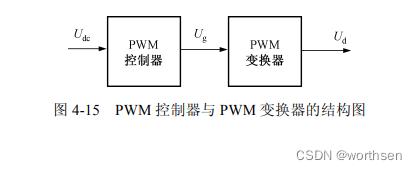
1．PWM 控制与 PWM 变换器的结构图
图 4-15 所示的是 PWM 控制器与 PWM 变换器的结构图，输入是 $U_{dc}$，控制是 $U_g$，输出是 $U_d$。

4.2 闭环调速系统与调速控制器

4.2.1 闭环调速系统

按照调节器的个数和功能，闭环调速系统可以分为单闭环调速系统、双闭环调速系统和多闭环调速系统。

1. 单闭环调速系统
   单闭环调速系统有速度、位置、电压、电流、电压变化率和电流变化率等类型，本书中除了特别说明，单闭环调速系统通常指的是速度调节器为主的系统。
2. 双闭环调速系统
   双闭环调速系统通常有：
   ①位置、电流环双闭环调速系统；
   ②速度、电流环双闭环调速系统；
   ③电压、电流环双闭环调速系统；
   ④电压、电流变化率环双闭环调速系统。
   通常，若无特殊指明，双闭环调速系统指的是速度、电流环双闭环调速系统。
3. 三闭环调速系统
   常见的三闭环调速系统有：
   ①位置、电压、电流环三闭环调速系统；
   ②速度、电压、电流环三闭环调速系统；
   ③速度、电流、电流变化率环三闭环调速系统。
   若无特别指明，三闭环调速系统指的是速度、电压、电流环三闭环调速系统。

在图 4-18 中，对直流调速系统进行了汇总。

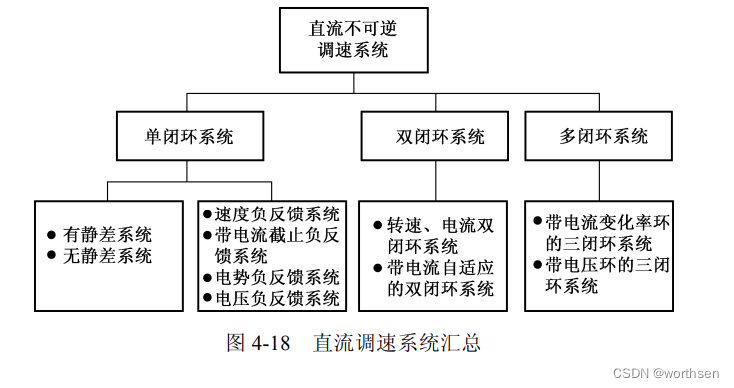
1．单闭环调速系统

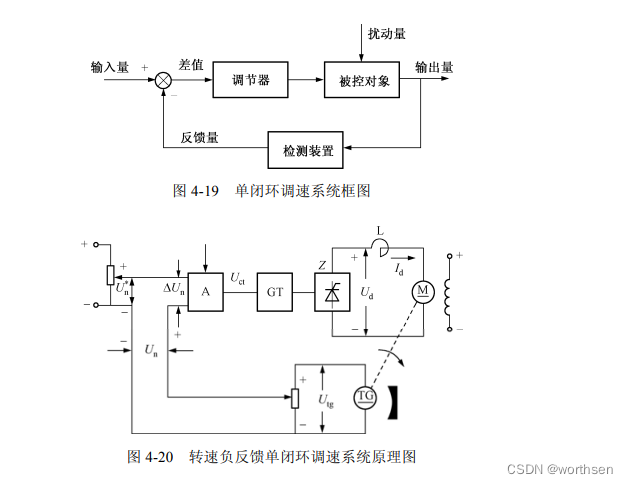
2．速度、电流双闭环调速系统
速度、电流双闭环调速系统具有如下特点：①系统的被调节量是转速，所检测的误差是转速，要消除的也是扰动对转速的影响；②速度单闭环调速系统不能控制电流（或转矩）的动态过程。

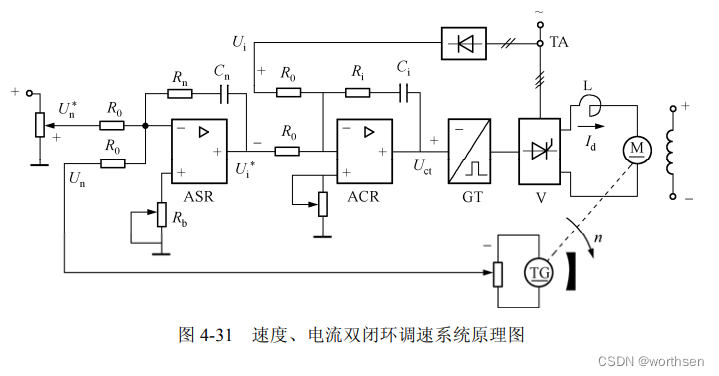
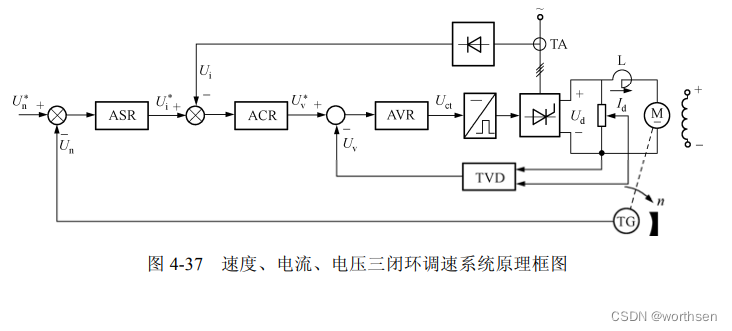
3．速度、电流、电压三闭环调速系统
速度、电流、电压三闭环调速系统是为了追求更高的调速控制性能，在速度环、电流环的基础上引入电流变化率或者电压环。

5 交流电机控制技术

交流电机具有结构简单、使用与维护方便等特点，在风机、水泵、压缩机、输送机等领域使用广泛。

5.1 交流电机调速系统基本理论

交流电机主要分为异步交流电机和同步交流电机两大类。异步交流电机有鼠笼式和绕线式；同步交流电机有自控式、他控式和永磁式。

5.1.1 研究交流电机的解耦问题的必要性

交流电机与直流电机相比，结构简单，使用维护方便，那么为什么早期交流电机调速却得不到应有的普及呢？主要有以下四个原因：
第一是数学模型，由于交流电机的特点是强耦合、时变、非线性，因此其数学模型描述复杂，使得电机转矩控制困难；
第二是控制器技术，需要解算的对象相对于直流电机而言复杂，要求交流电机的控制器功能强大；
第三是电力电子技术，早期电力电子器件的功能难以满足交流电机对 PWM 的要求；第四是检测技术，早期反馈检测元件达不到交流电机调速的要求。

6 伺服电机（servo motor ）控制技术

6.1 伺服控制系统概述

伺服意味着“伺候”和“服从”。广义的伺服控制系统指的是精确地跟踪或复现某个过程的反馈控制系统，也可称为随动系统。而狭义的伺服控制系统指的是，被控制量（输出量）是负载的线位移或角位移，当位置给定量（输入量）任意变化时，系统使输出量快速而准确地复现输入量的变化，又称为位置随动系统。
1．伺服控制系统的基本要求
伺服控制系统的基本要求是：①稳定性好；②精度高；③动态响应快；④抗扰动能力强。
2．伺服控制系统的基本特征
伺服控制系统的基本特征是：
① 必须具备高精度的传感器，能准确地给出输出量的电信号；
② 功率放大器及控制系统都必须是可逆的；
③ 足够大的调速范围及足够强的低速带载能力；
④ 快速的响应能力和较强的抗干扰能力。
3．伺服控制系统的组成
图 6-1 所示的是伺服控制系统的框图。由图可见，系统由五大部件组成，控制器、驱动装置、伺服电机、机械传动机构和传感器。

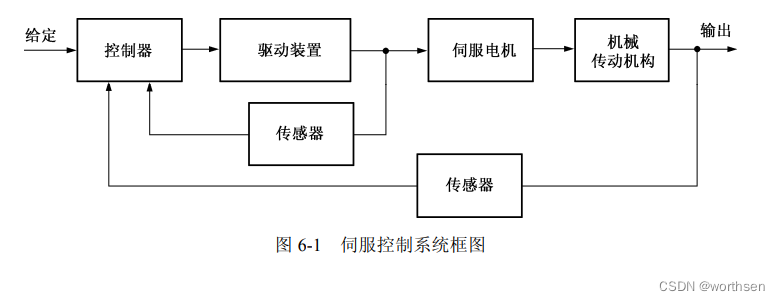
1. 控制器
   控制器是伺服控制系统的关键所在，伺服控制系统的控制规律体现在控制器上。控制器依据任务需求，结合传感器的反馈情况，得出偏差信号，经过必要的控制算法，产生驱动装置的控制信号。
2. 驱动装置与伺服电机
   驱动装置主要起功率放大作用。根据不同的伺服电机，驱动装置控制伺服电机的转矩和转速，以满足伺服控制系统实际的需求。伺服电机是伺服系统的执行元件，通常用于精密机械的传动控制。
3. 传感器
   传感器的检测精度和准确度对于伺服控制系统的性能至关重要。通常，把控制器、驱动装置与传感器预处理电路整合在一起，制成一个标准产品，即伺服驱动器。
4. 机械传动机构
   机械传动机构是实现控制的直接物理形式。为了满足各种功能需求，离不开机械机构的保证。高精度的机械传动是实现精密控制的坚实基础。

6.2 伺服控制系统的数学模型

6.2.1 直流伺服控制系统的数学模型

1．直流伺服控制系统的静态结构框图
2．直流伺服控制系统的数学模型
3．带电流环控制的直流伺服控制系统

6.2.2 交流伺服控制系统的数学模型

1．异步交流伺服电机按转子磁链定向的数学模型
2．交流伺服控制系统控制对象的统一模型

6.3 永磁同步电机交流伺服控制

1．永磁同步电机
交流伺服电机由于克服了直流伺服电机电刷和机械换向器带来的各种限制，因此在工厂自动化中获得了广泛的应用。在数控机床、工业机器人等小功率应用场合，转子采用永磁材料的同步伺服电机驱动比异步笼型伺服电机有更为广泛的应用，这主要是因为现代永磁材料性能不断提高，价格不断下降，相对异步电机来说控制也比较简单，容易实现高性能的优良控制。
2．PMSM 伺服控制系统的数学模型
3．PMSM 的等效电路
4．PMSM 的矢量控制
5．PMSM 解耦状态方程

6.4 伺服控制系统的设计

6.4.1 单环位置伺服控制系统设计

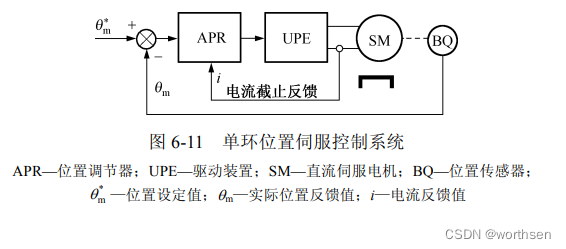
对于直流伺服电机可以采用单环位置伺服控制方式——直接设计位置调节器 APR，如图 6-11 所示。为了避免在过渡过程中电流冲击过大，应采用电流截止反馈保护，或者选择允许过载倍数比较高的伺服电机。
由于交流伺服电机具有非线性、强耦合的性质，因此单环位置伺服控制方式难以达到伺服控制系统的动态要求，故一般不采用单环位置伺服控制。

作为动态校正和加快跟随作用的位置调节器，常选用 PD 或 PID 调节器，或者在位置反馈的基础上附加位置微分反馈（即转速反馈）。采用微分控制是为了提高响应跟随的快速性。若要求系统对负载扰动无静差，应选用 PID 调节器。

6.4.2 双环伺服控制系统设计

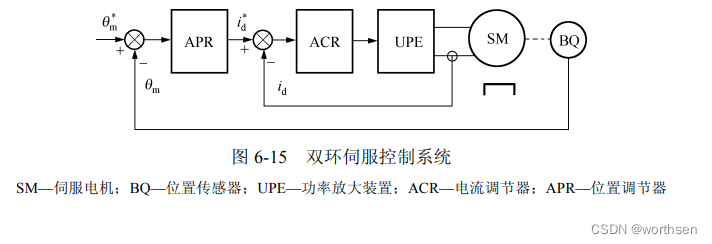
如前所述，电流环控制可以抑制启、制动电流，加快电流的响应。对于交流伺服电机，电流环还可以改造受控对象，实现励磁分量和转矩分量的解耦，得到等效的直流电机模型。因此，可以在电流环作为内环的基础上，直接设计位置调节器，构成外环，从而形成位置、电流双环伺服控制系统。其结构如图 6-15 所示。

6.4.3 三环伺服控制系统设计

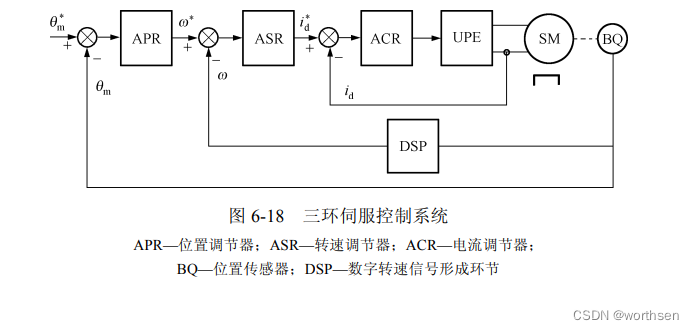
在位置环、电流环伺服控制系统的基础上，再设一个速度环，从而形成三环伺服控制系统，如图 6-18 所示。其中，位置调节器 APR 是位置环的校正装置，其输出限幅值决定着电机的最高转速。

6.4.4 PMSM 伺服控制系统设计

1. 影响电流环性能的主要因素
   影响电流环性能的主要因素是反电动势的干扰、PI 调节器的影响及零点漂移。
2. 电流环 PI 综合设计

6.5 标准商用伺服驱动器应用简介

伺服驱动器作为一种标准商品，已经得到广泛应用。目前，生产各种伺服电机和配套伺服驱动器的公司很多，如德国的力士乐、西门子，日本的三菱、安川、松下、欧姆龙，韩国的 LG 等。

标准商用伺服驱动器的四种工作模式：
(1) 位置控制方式
(2) 速度控制方式
(3) 转矩控制方式
(4) 全闭环控制方式

7 检测技术

7.1 直线位移检测

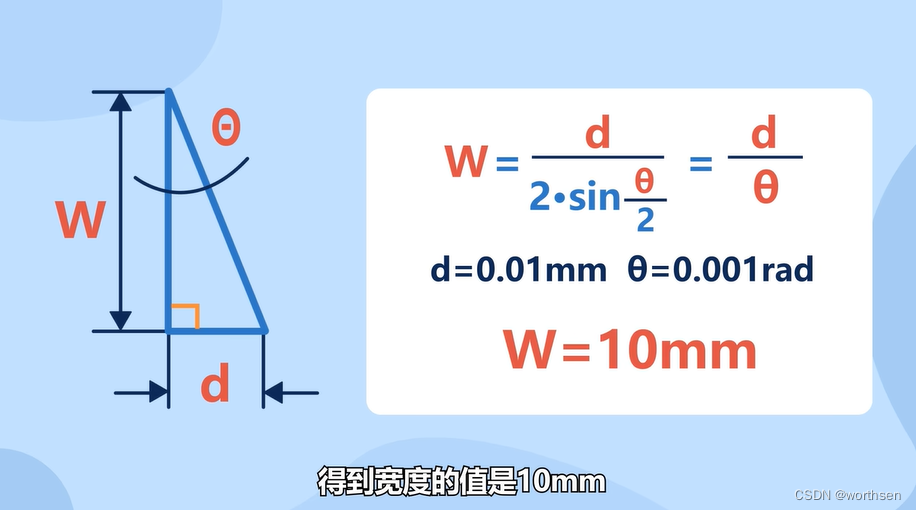
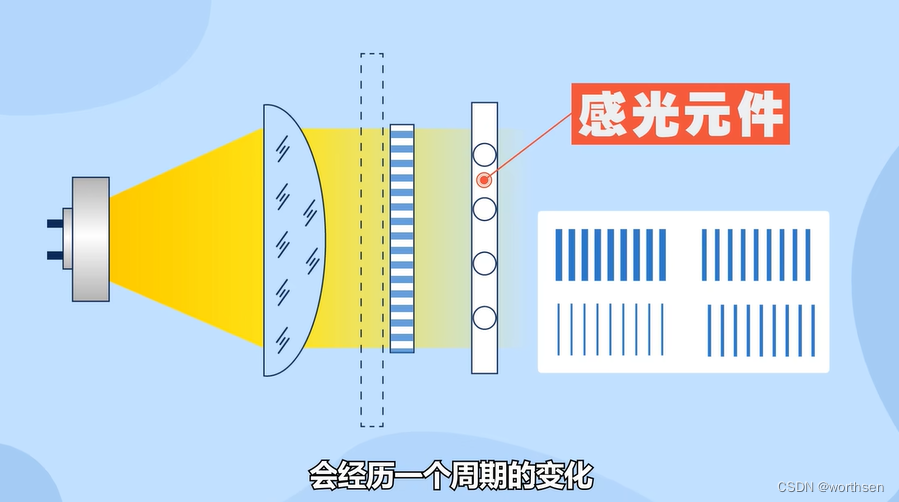
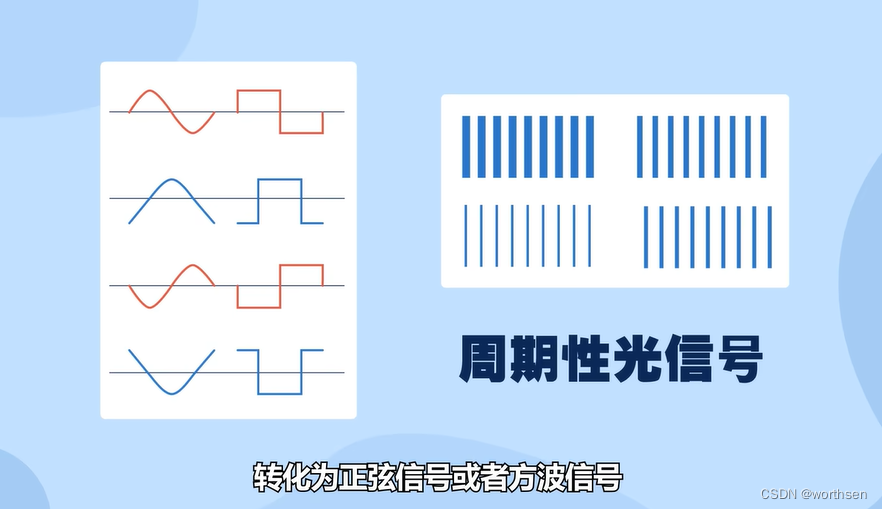
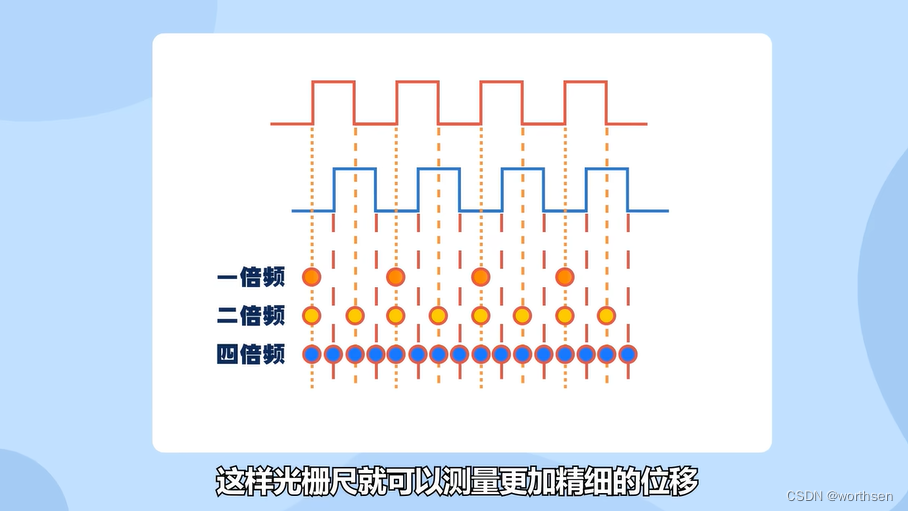
7.1.1 光栅

数据采集卡与【编码器】【光栅尺】【位移采集】

光栅尺是编码器的一种。

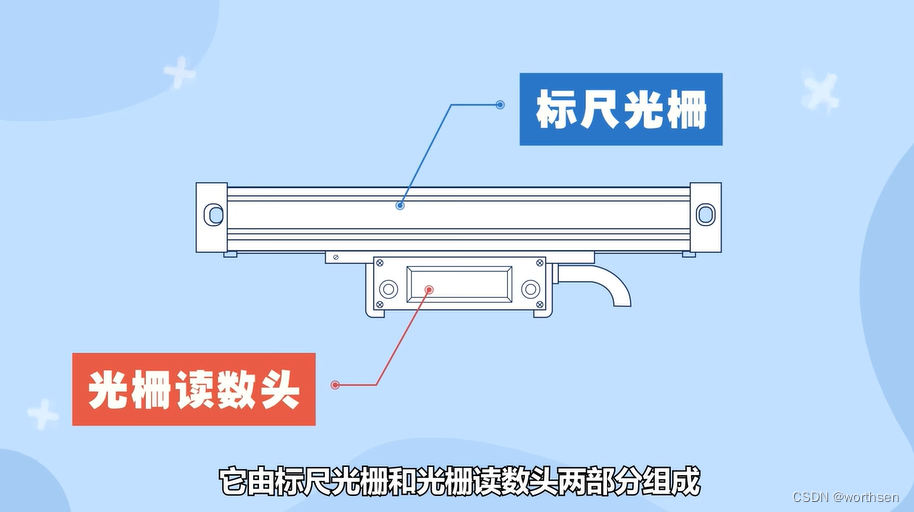
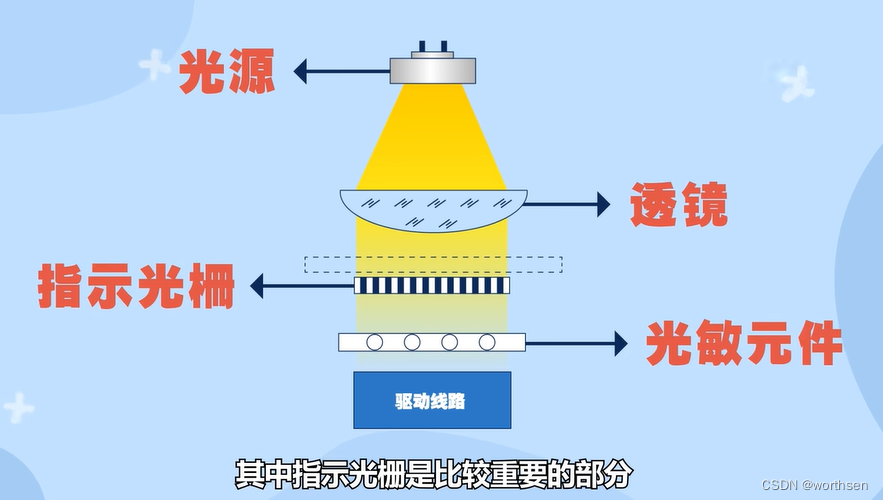
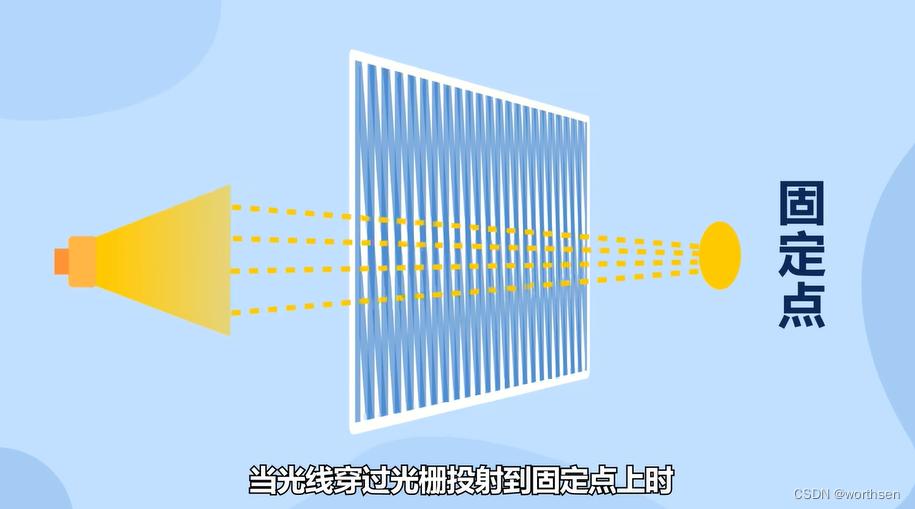
7.1.2 感应同步器

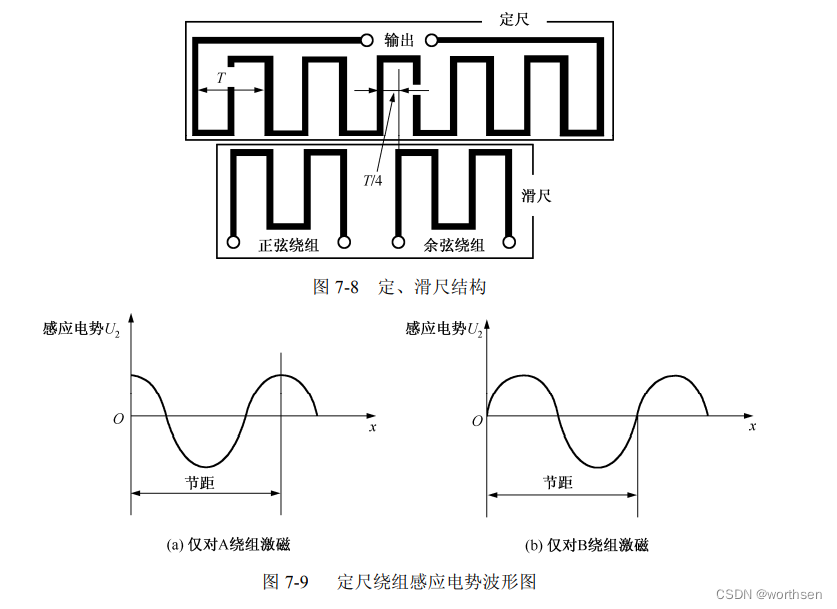
感应同步器是利用电磁感应原理把两个平面绕组间的位移转换成电信号的一种位移传感器。

7.1.3 磁栅式传感器

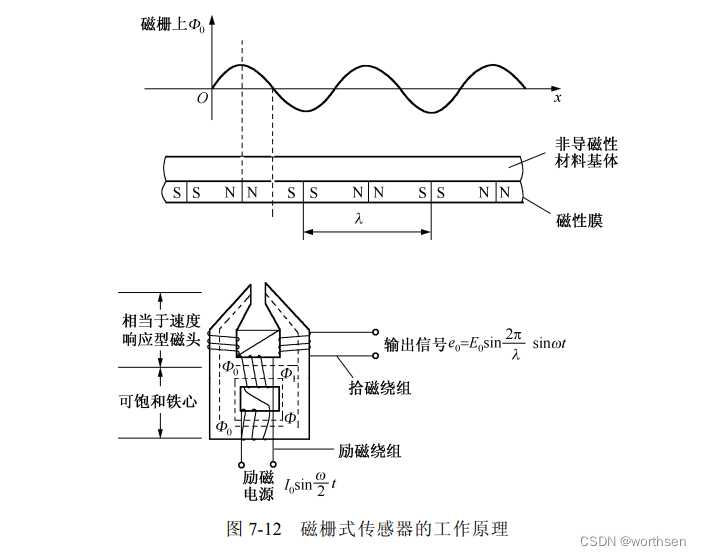
磁栅式传感器是利用磁栅与磁头的磁作用进行测量的位移传感器。它是一种新型的数字式传感器，成本较低且便于安装和使用。当需要时，可将原来的磁信号（磁栅）抹去，重新录制。还可以安装在机床上后再录制磁信号，这对于消除安装误差和机床本身的几何误差，以及提高测量精度都是十分有利的。磁栅式传感器可以采用激光定位录磁，而不需要采用感光、腐蚀等工艺，因而精度较高，可达±0.01 mm/m，分辨率为 1～5 μm。

7.2 角位移检测

7.2.1 旋转变压器

旋转变压器是一种利用电磁感应原理将转角变换为电压信号的传感器。由于它结构简单，动作灵敏，对环境无特殊要求，输出信号大，抗干扰好，因此被广泛应用于机电一体化产品中。


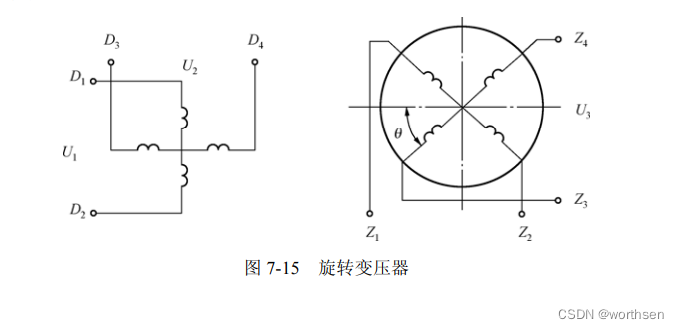
旋转变压器适用于所有使用光电编码器的场合，特别是高温、严寒、潮湿、高速等光电编码器无法正常工作的场合。由于旋转变压器的以上特点，它被广泛应用在伺服控制系统、机器人系统、机械工具、汽车、电力、冶金、纺织、印刷、航空航天、船舶、兵器、电子、冶金、矿山、油田、水利、化工、轻工、建筑等领域的角度或位置检测系统中。

7.2.2 光电编码器

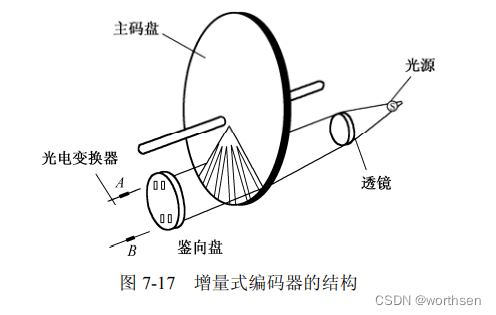
光电编码器是一种码盘式角度-数字检测元件。它有两种基本类型：增量式编码器、绝对式编码器。增量式编码器具有结构简单、价格低、精度易于保证等优点，所以目前采用最多。绝对式编码器能直接给出对应于每个转角的数字信息，便于计算机处理，但当进给数大于一转时，必须进行特别处理，而且必须用减速齿轮将两个以上的编码器连接起来，组成多级检测装置，使其结构复杂、成本高。
1．增量式编码器

2．绝对式编码器

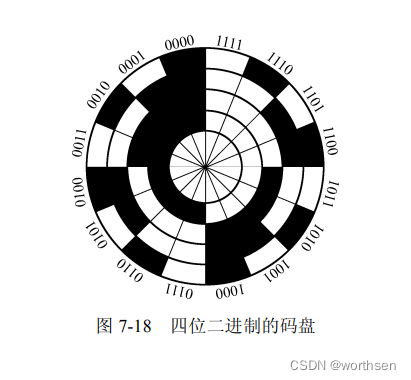
1. 循环码盘
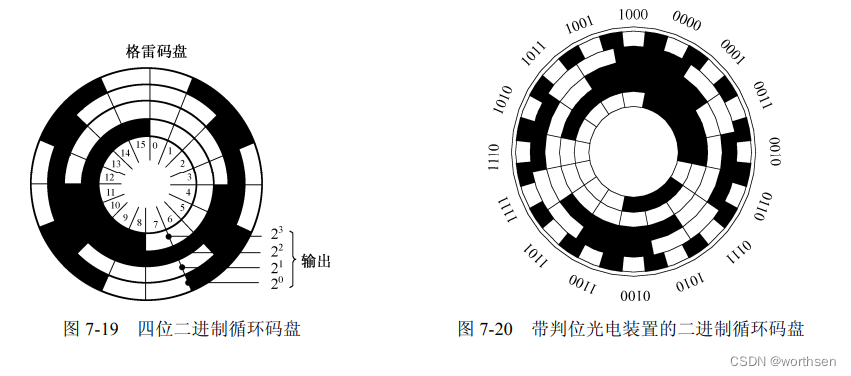
   循环码习惯上又称为格雷码，它也是一种二进制编码，只有“0”和“1”两个数。图 7-19 所示的是四位二进制循环码盘。这种编码的特点是任意相邻的两个代码间只有一位代码有变化，即“0”变为“1”或“1”变为“0”。因此，在两数变换过程中，所产生的读数误差最多不超过“1”，只可能读成相邻两个数中的一个数。所以，它是消除非单值性误差的一种有效方法，码盘由外至内表征的数制的权位分别是 $2^0、2^1、2^2、2^3$，其表述的数值是 0～15 或者十六进制的 0～F。
2. 带判位光电装置的二进制循环码盘
   这种码盘是在四位二进制循环码盘的最外圈再增加一圈信号位。图 7-20 所示的就是带判位光电装置的二进制循环码盘。该码盘最外圈的信号位上正好与状态交线错开，只有当信号位所处的光电元件有信号时才读数，这样就不会产生非单值性误差。
   

7.3 速度、加速度检测

7.3.1 直流测速发电机
7.3.2 光电式速度传感器
7.3.3 加速度传感器

7.4 力、力矩检测

在机电一体化工程中，力、压力和扭矩是很常用的机械参量。近年来，各种高精度的力和扭矩传感器的出现，更以其惯性小、响应快、易于记录、便于遥控等优点得到了广泛的应用。按其工作原理可分为弹性式、电阻应变式、电感式、电容式、压电式和磁电式等，而电阻应变式传感器应用较为广泛。
7.4.1 测力传感器
7.4.2 压力传感器
7.4.3 力矩传感器
7.4.4 力与力矩复合传感器

8 应用实例

补充

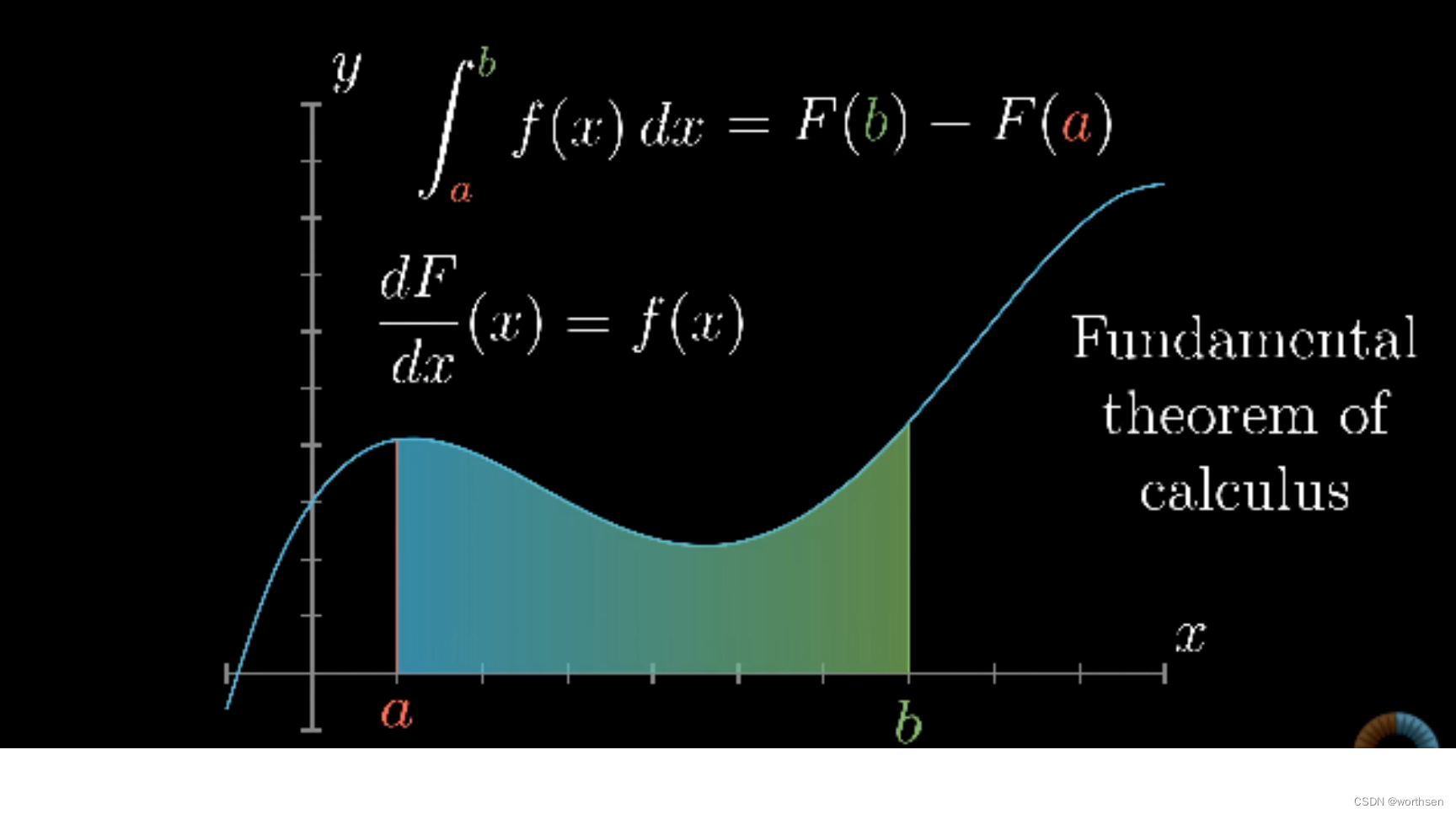
积分公式

$${\int }_a^{b}f(x)dx=F(b)-F(a)$$

电机分类

From

• 吐血整理最通俗易懂的电机控制讲解（二）-你知道BLDC和PMSM的区别吗？
• 【机电杂谈2】BLDC和PMSM的特点和区别
• 机器人开发–伺服电机介绍
• 机器人开发–有刷电机 与 无刷电机
• 转稚晖军大佬 --【自制FOC驱动器】深入浅出讲解FOC算法与SVPWM技术

有刷直流电机、无刷直流电机、永磁同步电机由于其结构和输出特定的不同也被应用到不同的场合。常见的玩具和家电中能看到大量的有刷直流电机和无刷直流电机，而永磁同步电机主要应用在高精度的工业伺服和电动汽车领域。

从控制精准度上说，则伺服调速精度最高，步进次之，直流有刷及无刷电机最低。伺服电机一般都是被使用在精度要求高的场合，而无刷电机就只用在精度不是特别高的地方了，步进电机居中，但步进电机的转速没有无刷电机快。

有刷直流电机和无刷直流电机

有刷直流电机是结构和控制最简单的直流电机，电机主要依靠电刷进行电流换向。使用一个电磁继电器或者半导体开关即可对其进行启停控制；如果有正反转要求，则需要4颗半导体开关器件构成H桥的形式进行正反电流的控制。使用半导体开关可以很方便的实现有刷电机的调速（通过控制PWM的占空比进行调节），因此基本上现在对于有刷电机都是采用功率MOSFET进行调速和控制。

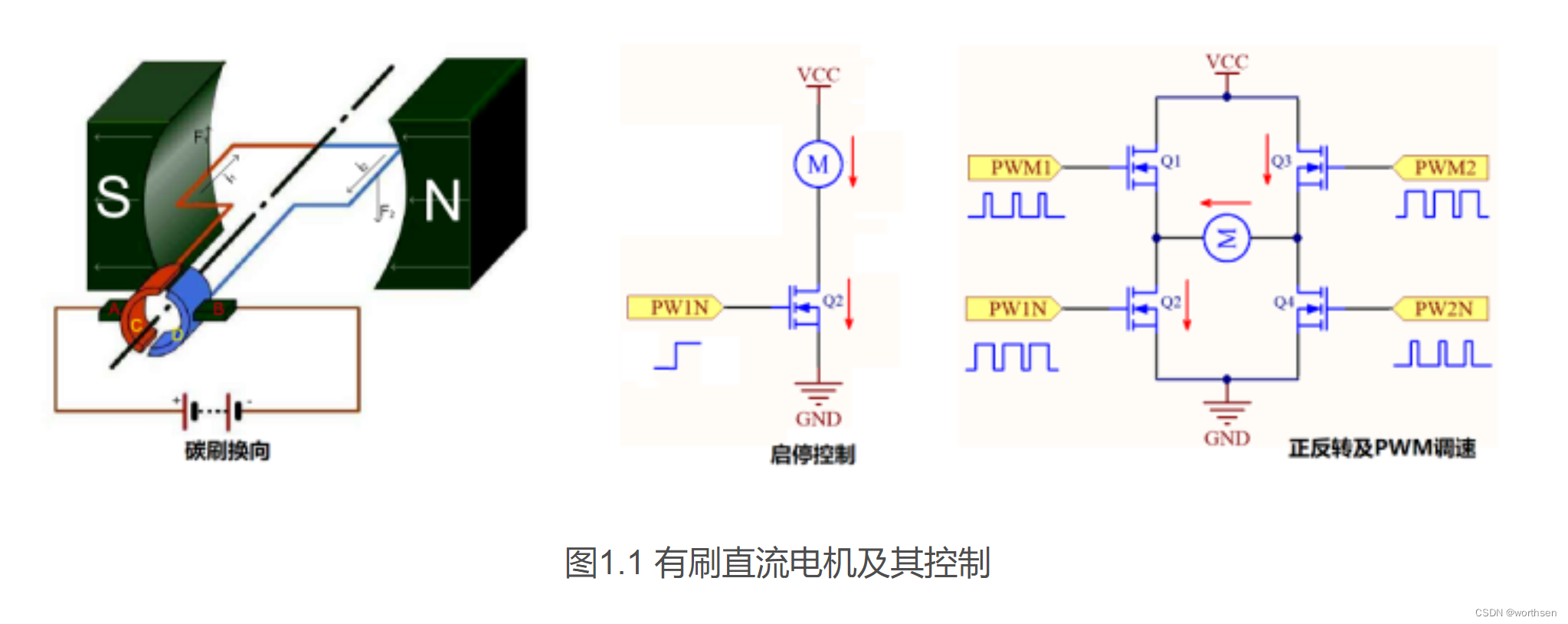
有刷电机的电刷是一个易损件，因此有刷电机的使用寿命有限，并且碳刷换向过程中释放出电火花无法应用在类似煤矿、油田这类具有易燃易爆物质的场景中。

无刷直流电机（BLDC）的出现得益于开关半导体和电机控制芯片的发展，无刷直流电机取消的电刷换向，而使用功率半导体进行换向，驱动拓扑几乎都是三相两电平的结构，也就是我们常说的三相桥。通过控制三相桥的导通时序和方向，产生牵引转子永磁体的磁场，在三相桥的切换过程中能够保持定子磁场和转子磁场一个相对比较稳定的位置（90°±30°），如图1.2所示。

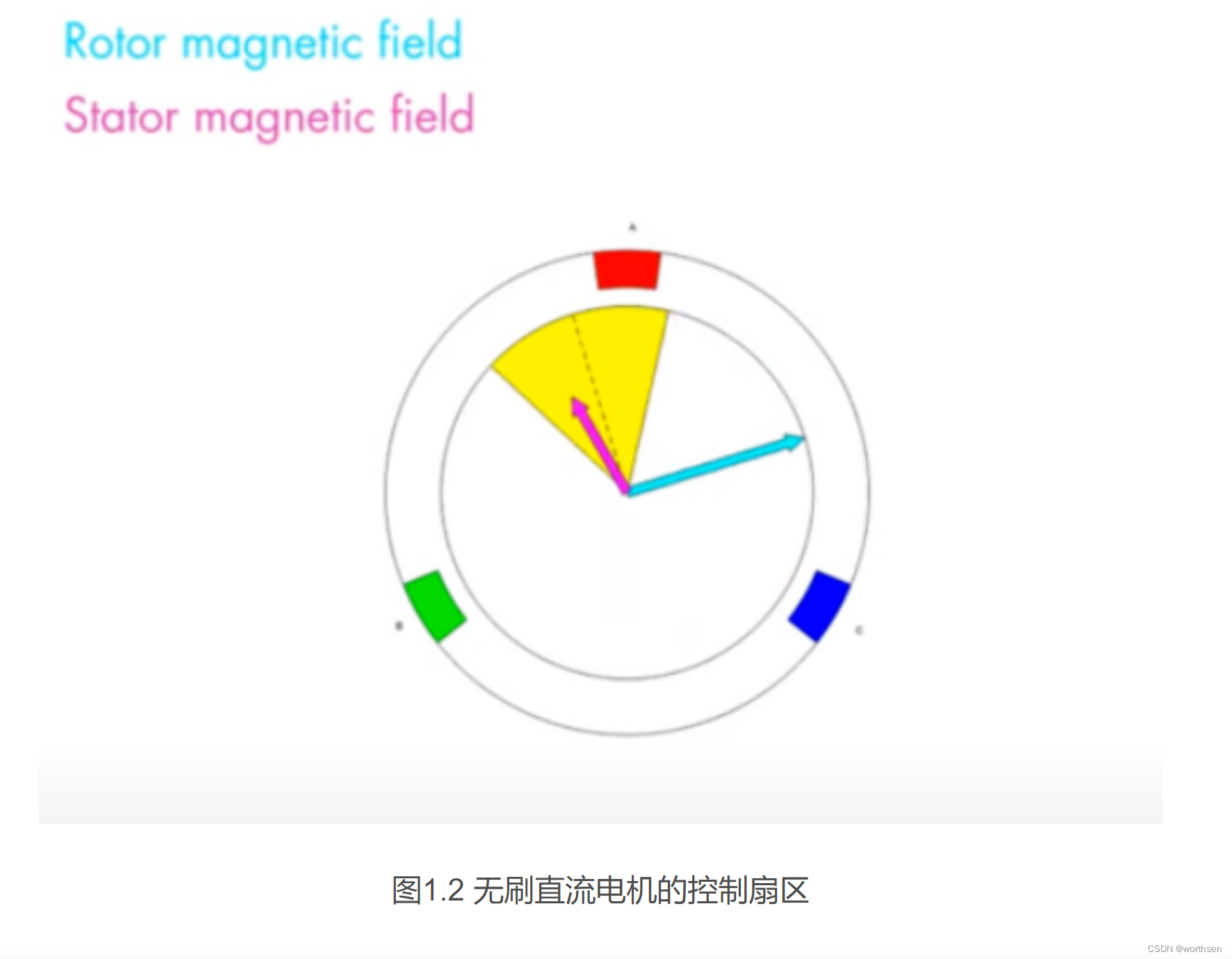
无刷直流电机（BLDC）反电势是梯形波形，这样就可以采用具有矩形波形的直流电压来生成低转矩纹波的旋转磁场。 由于所施加的矩形电压很容易产生，比如随便一款MCU，或者C2000系列DSP乃至于51单片机都可以产生这种PWM波，所以电机的控制和驱动变得简单，同时在相同功率输出下BLDC能做的更轻。像无人机，洗脱一体机等，只需要电机调速，无需伺服定位，不需要很高的控制精度，这种功率小，转速高的场合就用BLDC。

BLDC和PMSM区别

BLDC（Brushless Direct Current Motor），即无刷直流电机。
PMSM（permanent-magnet synchronous motor），即永磁同步电机。

真正区分两者的参数是"反电势"。

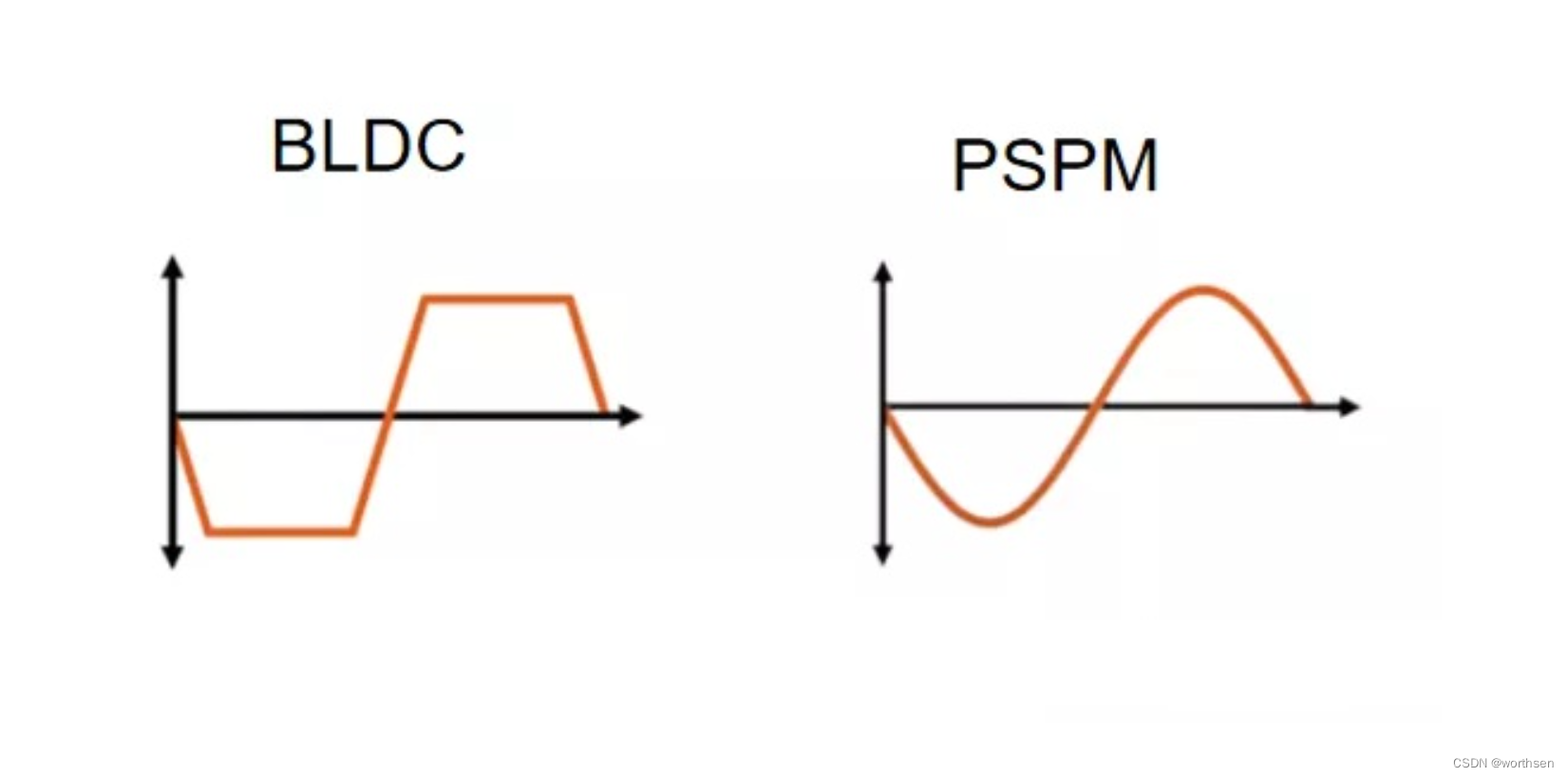
BLDC反电势波形是梯形，而PMSM反电势波形是正弦。所以虽然都是永磁同步电机，为了区分还是要进行命名区分的，因此就出现了目前常说的BLDC和PMSM。

如图2.2，我们大致感受下两种电机的结构差异。
无刷直流电机的结构相对比较简单，定子线圈大多采用图2.2左所示的集中式绕组结构，该结构工艺简单，成本低廉，是应用范围最广的BLDC定子结构。
永磁同步电机的定子绕组更加“分布、均匀”，直觉上来看PMSM运行应该更加安静、顺滑。

FOC 和 Six-Step

FOC
FOC（Field-Oriented Control），直译是磁场定向控制，也被称作矢量控制（VC，Vector Control），是目前无刷直流电机（BLDC）和永磁同步电机（PMSM）高效控制的最优方法之一。FOC旨在通过精确地控制磁场大小与方向，使得电机的运动转矩平稳、噪声小、效率高，并且具有高速的动态响应。
常用方案：

• 位置编码器：通过高精度的光栅感应定子旋转过程中引起的数字编码变化，从而解析转子位置信息，一般应用在高精度的伺服系统中。
• Hall磁编码器：通过在电机轴的端部安装的永磁体旋转，引起Hall传感器的磁感线变化，从而解析转子位置信息，一般应用在中小功率泵类驱动系统中。
• 旋转变压器：电机轴的旋转引起旋转变压器感应电压的变化，通过一定的解码算法，从而解析转子位置信息，一般应用在高可靠性、高寿命的电动汽车系统中。
• 观测器位置算法：这是一种无位置传感器的方法，通过电机模型的建模计算出反电动势的变化，从而解析出转子的位置信息，该方法可靠性高，成本低，维护方便，也是电机控制最火热的方向。笔者认为，该方案主要取代的是Hall编码器的应用市场，对于高精度，高可靠性，快速动态性能的场合应用还是比较有限。

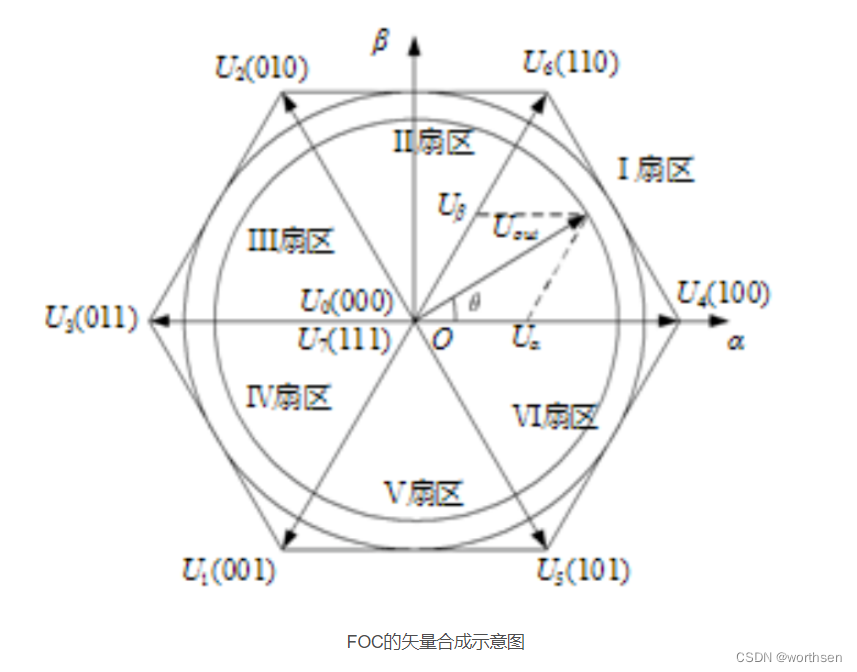
Six-Step
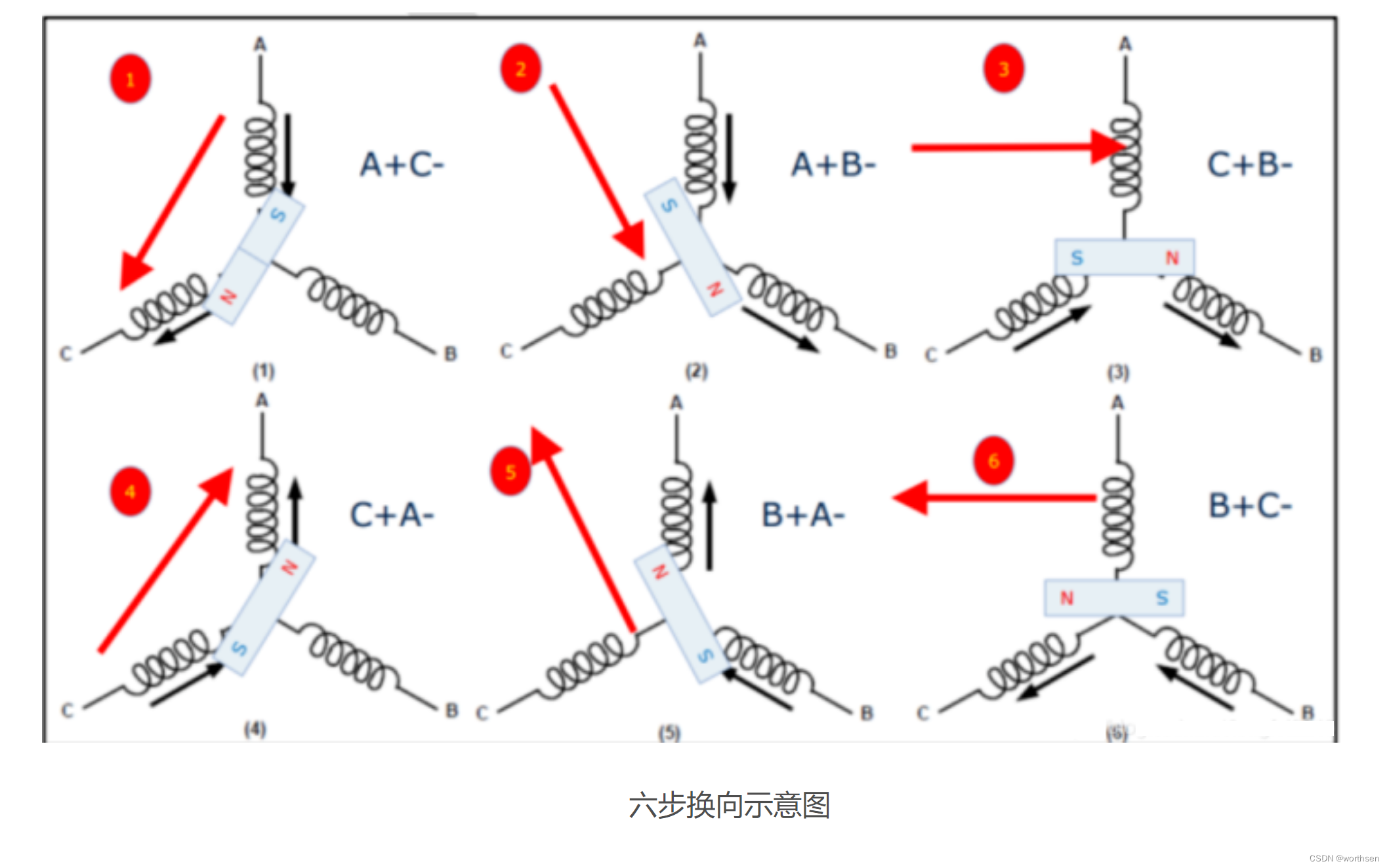
由于BLDC的反电动势是梯形波，存在这样快速的“换向点”，因此检测BLDC的位置相对来讲是比较简单：可以在定子内嵌入逻辑霍尔传感器，检测转子磁钢的位置进行直接的定位；也可以通过检测反电动势的换向点进行无传感器的位置检测。

该控制的本质还是基于位置信息的通电逻辑控制，因此该控制方法对芯片的要求极低，并且不需要额外的传感器成本，因此是BLDC最主流的控制方案。但是该控制的颗粒度很大，一般来讲转矩脉动和噪音都是比较大的，对于大功率，高性能的应用场合出现的频率比较小。

FOC驱动器和无刷电调的区别

无人机中对于无刷电机的驱动使用的是电子调速器（ESC）也就是我们常说的电调。
电调使用方波来控制电机，控制简单，不过声音大，精度低；
FOC使用正弦波来控制电机，控制复杂，声音小，精度高。

参考

1、wiki–运动控制
2、《运动控制系统》班华 李长友 主编
3、蛮力硬推定积分基本公式
4、微积分的本质（八）：积分与微积分基本定理
5、运动控制中的轨迹曲线
6、「 运动控制 」“运动控制、过程控制、动态控制、运动规划、轨迹规划、路径规划”浅谈
7、吐血整理最通俗易懂的电机控制讲解（二）-你知道BLDC和PMSM的区别吗？
8、【机电杂谈2】BLDC和PMSM的特点和区别
9、航模电机为什么多用BLDC，而不是PMSM？
10、机器人开发–伺服电机介绍
11、机器人开发–有刷电机 与 无刷电机
12、转稚晖军大佬 --【自制FOC驱动器】深入浅出讲解FOC算法与SVPWM技术
13、数据采集卡与【编码器】【光栅尺】【位移采集】
14、我理解的运动控制系统
15、运动控制与系统
16、机器人的运动控制系统（一）——概述
17、什么是运动控制系统