一、问题场景描述

在做角色菜单按钮权限时，多数采用树结构勾选数据，这里使用了element中的el-tree。如下图：
1、我给角色1勾选了权限列表数据的前三行， 点击弹框的确定

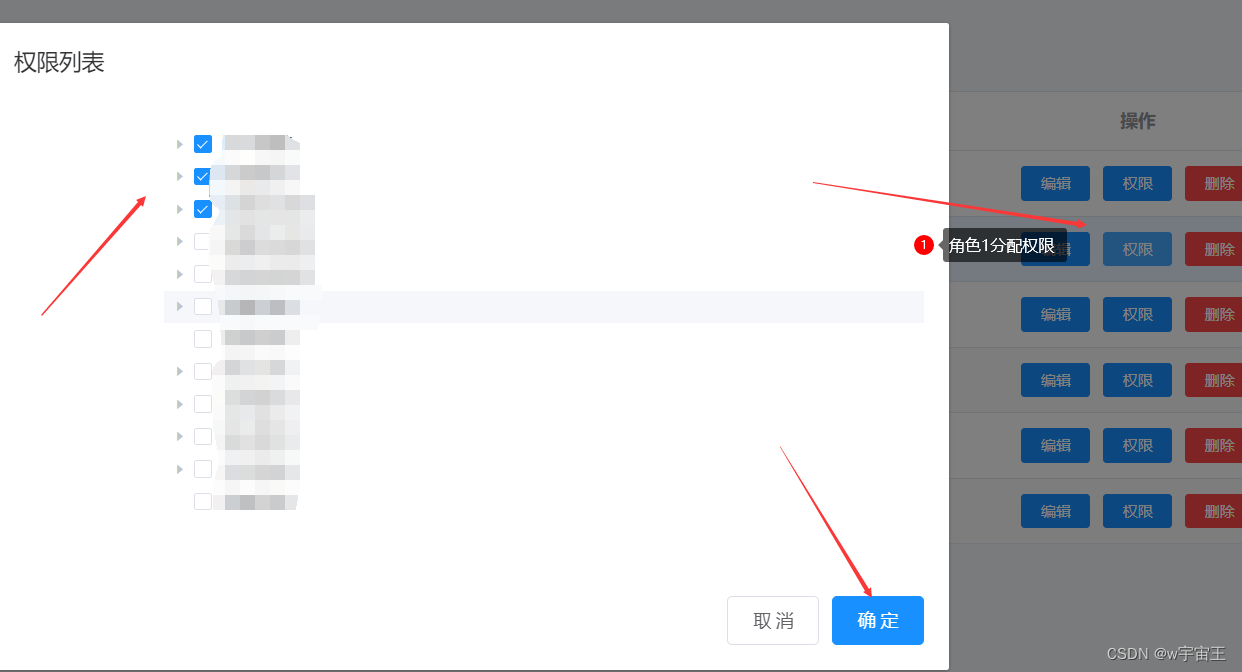
2、紧接着点击角色2的权限按钮，给角色2分配修改权限数据（后三行是之前设置的 此刻回显的数据） 但是 当我点击角色2的权限按钮，弹出弹框时，角色1的数据 也渲染到树形结构上了。

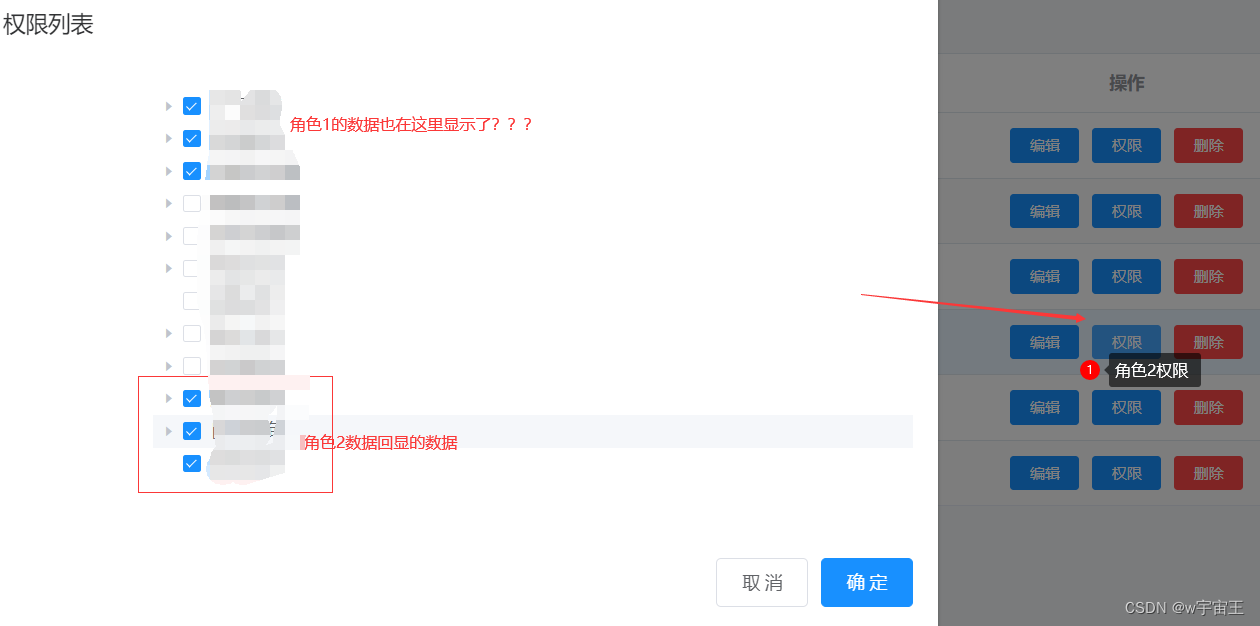
3、此时我更多考虑的是 无非就是 无赋值时未清空上一次的数据 ，所以我接下来在 能初始化 数据的地方都设置了 如下代码

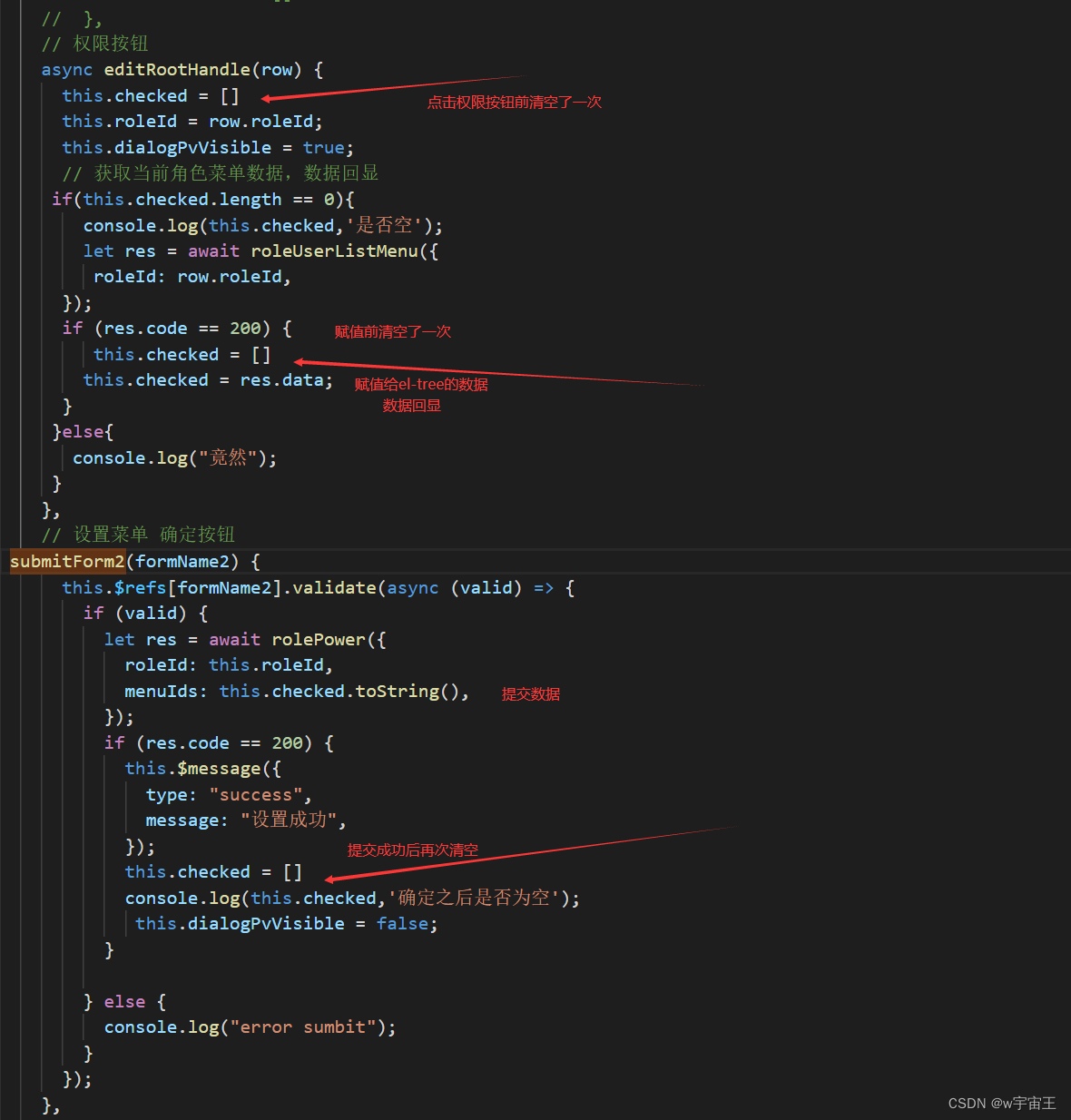
两个函数中 打印 this.checked 都是空了 但是页面 回显数据时依旧有哪个问题

console.log(this.checked)

4、此刻没什么想法 感觉是很简单的问题 也没好意思问同事，在我愁眉苦脸时，脑袋里浮现了一位姐姐，我询问她。
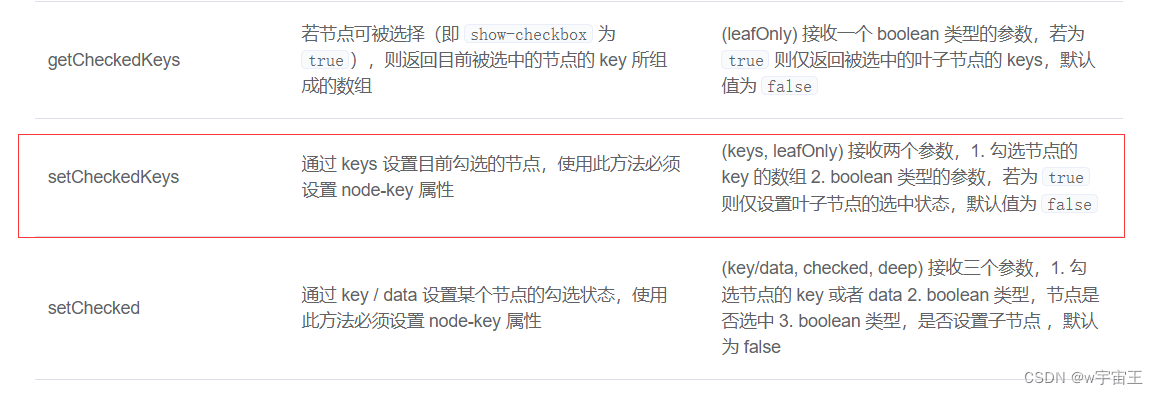
她说：你的 checked的数据是不是绑定在:default-checked-keys这个上？
我一看我上面引入的代码还真是，代码如下：

    <el-dialog title="权限列表" :visible.sync="dialogPvVisible" :close-on-click-modal = "false" :before-close="handleClose" :show-close = false><el-form :model="ruleForm2" :rules="rules2" ref="ruleForm2"><el-form-item prop="AccessMenu" :label-width="formLabelWidth"><el-treeref="tree":data="ruleForm2.AccessMenu":props="defaultProps"show-checkboxnode-key="menuId"class="permission-tree"@check="currentChecked":default-checked-keys="checked"/></el-form-item></el-form><div slot="footer" class="dialog-footer"><el-button @click="resetForm2('ruleForm2')">取 消</el-button><el-button type="primary" @click="submitForm2('ruleForm2')">确 定</el-button></div></el-dialog>

她又说：那你清空肯定不行呀，还是要调用这棵树本身的清空方法，因为那个只是默认展示的数据，再次点击，组件缓存了，当然组件选中的子节点也缓存了，所以你还是得调用tree本身的清空方法进行清空
5、调用 tree本身 setCheckedKeys 清空方法

 // 设置菜单 确定按钮submitForm2(formName2) {this.$refs[formName2].validate(async (valid) => {if (valid) {let res = await rolePower({roleId: this.roleId,menuIds: this.checked.toString(),});if (res.code == 200) {this.$message({type: "success",message: "设置成功",});this.SetCheckedKeys()this.dialogPvVisible = false;}} else {console.log("error sumbit");}});},// tree自身的清空方法SetCheckedKeys() {this.$refs.tree.setCheckedKeys([]);},

就这么简单，唉！