本题链接:卡码网KamaCoder
题目: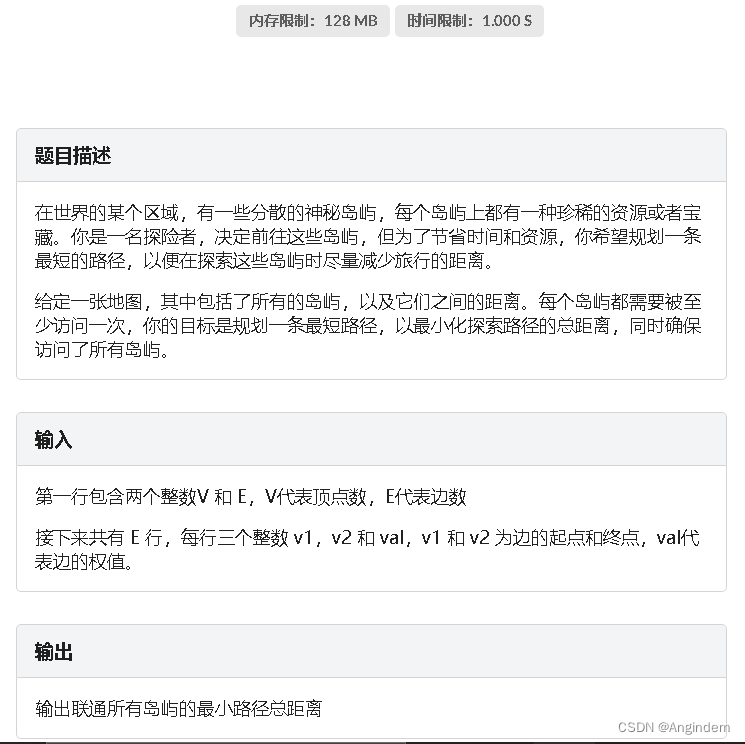
样例:
|
| 6 |
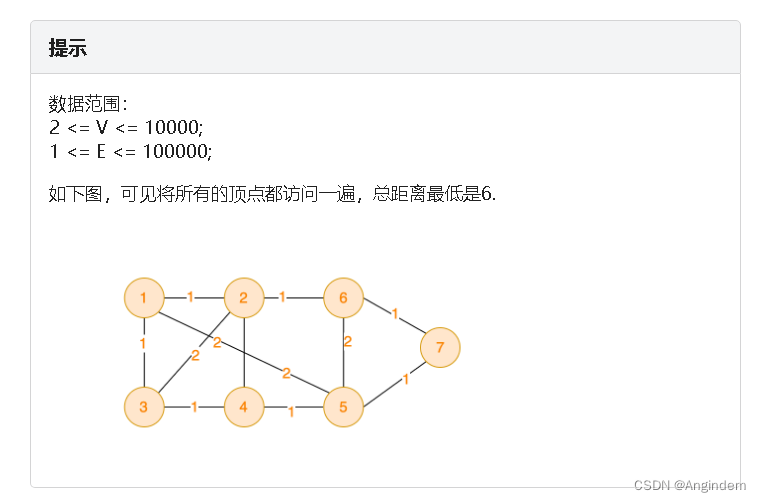
思路:
由题意,这里是需要遍历完全部的顶点,求遍历完全部点的花费最短距离。
从题干‘每个顶点都要访问一遍’,我们就应该联想到最小生成树,最小生成树中,有朴素版Prim最小生成树算法,和并查集的优化版Kruskal算法,由于这里的数据范围较大,所以我们应该使用并查集的优化版Kruskal算法。
代码详解如下:
#include <iostream>
#include <vector>
#include <queue>
#include <cstring>
#include <algorithm>
#include <unordered_map>
#define endl '\n'
#define YES puts("YES")
#define NO puts("NO")
#define umap unordered_map
#define All(x) x.begin(),x.end()
#pragma GCC optimize(3,"Ofast","inline")
#define IOS std::ios::sync_with_stdio(false),cin.tie(0), cout.tie(0)
using namespace std;
const int N = 2e6 + 10;int n,m,ans;// 定义结点之间和边权的关系结构体,并定义数组
struct Edge
{int a,b,w;// 定义排序规则,将边权最小的放在前面inline bool operator<(const Edge&t)const{return w < t.w;}
}edge[N];umap<int,int>p; // 标记的结点集合// 集合查找根节点函数
inline int Find(int &x)
{int t = x;while(x != p[x]) x = p[x];p[t] = x; // 剪枝路径操作return x;
}inline void Kruskal()
{// 排序好最小边权,我们优先连接最小边权的结点sort(edge,edge + m);// 初始化各个结点的连接根节点为本身for(int i = 0;i <= n;++i) p[i] = i;// 遍历每一条边权关系for(int i = 0;i < m;++i){// 获取存储关系的两个结点int a = edge[i].a;int b = edge[i].b;// 查找对应结点的根节点a = Find(a),b = Find(b);if(a != b){// 如果这两个结点未连接,我们将它们连接起来p[a] = b;ans += edge[i].w; // 累加最小边权}}return ;
}inline void solve()
{// 输入各个信息cin >> n >> m;for(int i = 0;i < m;++i){int a,b,w;cin >> a >> b >> w;// 存储记录好结点的边权关系edge[i] = {a,b,w};}// 开始克鲁斯卡尔算法Kruskal();// 输出答案cout << ans << endl;
}int main()
{
// freopen("a.txt", "r", stdin);IOS;int _t = 1;
// cin >> _t;while (_t--){solve();}return 0;
}