文章目录
- 📚降维的重要性
- 📚MDS、PCA
- 🐇MDS
- 🐇PCA
- 📚SNE
- 🐇总述
- 🐇SNE
- 🐇Symmetric-SNE
- 🐇T-SNE
📚降维的重要性
- 降维在数据分析和可视化领域中扮演着重要的角色。当面对高维数据时,我们往往面临着难以理解、分析和可视化的问题。高维数据不仅难以可视化,而且在某些机器学习算法中,高维度数据也可能导致过拟合问题。因此,降维可以帮助我们减少数据的维度,提高数据的可视化和分析能力,同时减少计算的复杂性。


📚MDS、PCA
- MDS (多维尺度变换) 和 PCA (主成分分析) 算法是常用的降维技术。
🐇MDS
-
MDS算法的基本思想是通过计算数据点之间的距离矩阵,并尝试在低维空间中重新构建数据点之间的距离矩阵。具体来说,MDS算法首先计算原始数据点之间的距离,然后通过优化算法在低维空间中找到合适的投影,使得在低维空间中的距离与原始距离最接近。

-
多维尺度分析MDS详解
-
数据降维-MDS
-
各种降维算法资源
🐇PCA
- PCA算法的基本思想是使用特征值分解来寻找数据中具有最大方差的主成分。PCA将高维数据通过线性变换映射到低维空间,并保留了最重要的特征。具体来说,PCA算法首先创建一个数据矩阵,然后通过减去均值来将数据中心化。接下来,它计算数据的协方差矩阵,并找到该矩阵的特征向量和特征值。最后,PCA算法根据特征向量将数据映射到新的低维空间。
- PCA主成分分析
📚SNE
🐇总述
- SNE、Symmetric-SNE和T-SNE的基本思想都是通过测量数据点之间的相似性并在低位空间中重建这种相似性来进行降维。
SNE(Stochastic Neighbor Embedding) 是一种降维算法,通过使用高维空间中数据点之间的相似性来在低维空间中表示数据。SNE算法基于两个关键思想:首先,相似的数据点在高维空间中应该保持相似的距离。其次,不相似的数据点在高维空间中应该保持不相似的距离。SNE通过最小化两个分布之间的KL散度来实现这些目标。Symmetric-SNE是对SNE算法的改进,通过在SNE映射中使用对称的条件概率来解决了SNE算法的对称性问题。这可以确保所得到的低维表示不会受到原始数据点的顺序变化的影响。T-SNE(t-Distributed Stochastic Neighbor Embedding) 是在SNE基础上发展而来的一种流行的降维算法。T-SNE使用t分布来替代SNE中的高斯分布,使得T-SNE能够更好地保留数据之间的局部结构。T-SNE通过优化KL散度来最小化高维和低维概率分布之间的差异。与SNE相比,T-SNE能够更好地处理非线性关系,并在可视化高维数据时提供更好的效果。
🐇SNE
- SNE算法的基本思想是通过最小化KL散度来在低维空间中表示高维数据的相似性。
-
计算高维空间中数据点之间的条件概率: P j ∣ i = exp ( − ∣ ∣ x i − x j ∣ ∣ 2 / 2 σ i 2 ) ∑ k ≠ l exp ( − ∣ ∣ x i − x k ∣ ∣ 2 / 2 σ i 2 ) P_{j|i} = \frac{{\exp(-||\mathbf{x}_i - \mathbf{x}_j||^2 / 2\sigma_i^2)}}{{\sum_{k \neq l}{\exp(-||\mathbf{x}_i - \mathbf{x}_k||^2 / 2\sigma_i^2)}}} Pj∣i=∑k=lexp(−∣∣xi−xk∣∣2/2σi2)exp(−∣∣xi−xj∣∣2/2σi2)

-
在低维空间中计算数据点之间的条件概率: Q j ∣ i = exp ( − ∣ ∣ y i − y j ∣ ∣ 2 ) ∑ k ≠ l exp ( − ∣ ∣ y i − y k ∣ ∣ 2 ) Q_{j|i} = \frac{{\exp(-||\mathbf{y}_i - \mathbf{y}_j||^2)}}{{\sum_{k \neq l}{\exp(-||\mathbf{y}_i - \mathbf{y}_k||^2)}}} Qj∣i=∑k=lexp(−∣∣yi−yk∣∣2)exp(−∣∣yi−yj∣∣2)

-
最小化KL散度: C o s t = K L ( P ∣ ∣ Q ) = ∑ i ∑ j P j ∣ i log P j ∣ i Q j ∣ i Cost = KL(P||Q) = \sum_i{\sum_j{P_{j|i} \log{\frac{{P_{j|i}}}{{Q_{j|i}}}}}} Cost=KL(P∣∣Q)=∑i∑jPj∣ilogQj∣iPj∣i
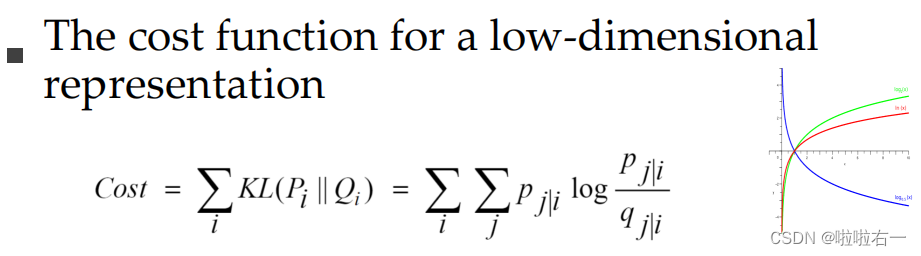
算法步骤:
- 初始化低维空间中的数据点坐标
- 计算高维空间中数据点之间的距离和条件概率
- 在低维空间中计算数据点之间的条件概率
- 最小化KL散度,通过梯度下降法更新低维空间中的数据点坐标
- 重复步骤3和4,直到满足停止条件
🐇Symmetric-SNE
- Symmetric SNE是SNE(Stochastic Neighbor Embedding)的一个简化版本,工作方式大致相同。
-
对于高维空间中的每一点i,都有一个条件概率选取其他的每一点j作为其邻居。此条件分布基于高维空间中的成对距离。
-
要得到i和j之间的对称概率,我们可以将两个条件概率相加并除以总的点数(点不能选择自己)。 这样可以确保所有的成对概率之和为1,所以它们可以被视为概率。

-
如果 p j ∣ i p_{j|i} pj∣i 表示 i 选择 j 的条件概率,那么对称概率 p i j p_{ij} pij 可以计算为 p i j = ( p j ∣ i + p i ∣ j ) / 2 N p_{ij} = (p_{j|i} + p_{i|j}) / 2N pij=(pj∣i+pi∣j)/2N,其中N是总的点数。
-
给每个数据点在低维空间中一个位置。在低维空间中对概率进行对称的定义。
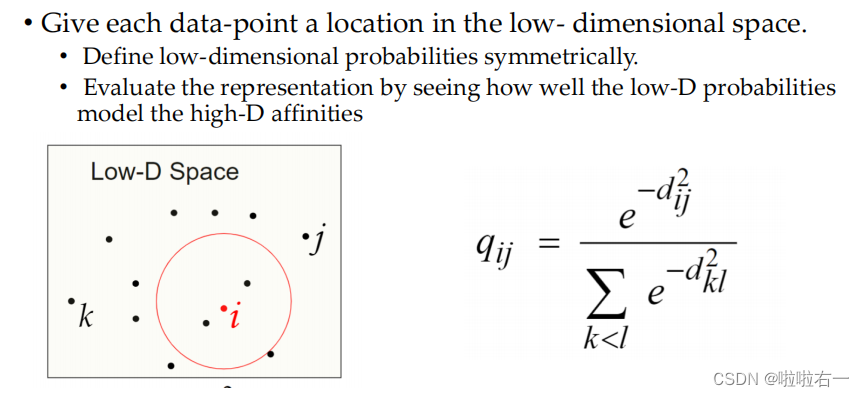
-
在低维空间中评估点的布局,检查低维空间的概率模型如何符合高维空间的相似性。
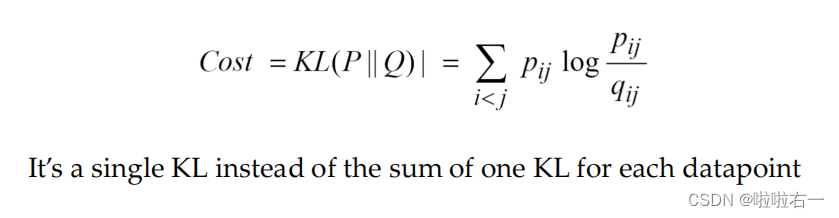
-
🐇T-SNE
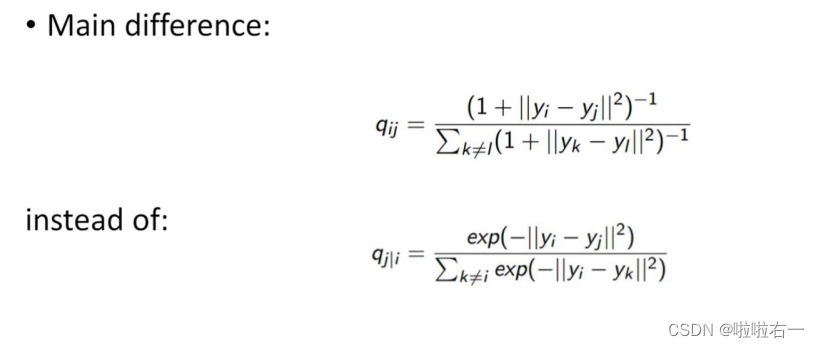
- Code and implementation for different languages
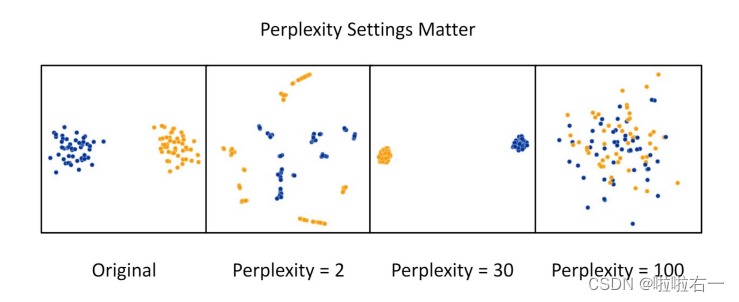
- Sigma is crucial a good example on how sigma affect mapping