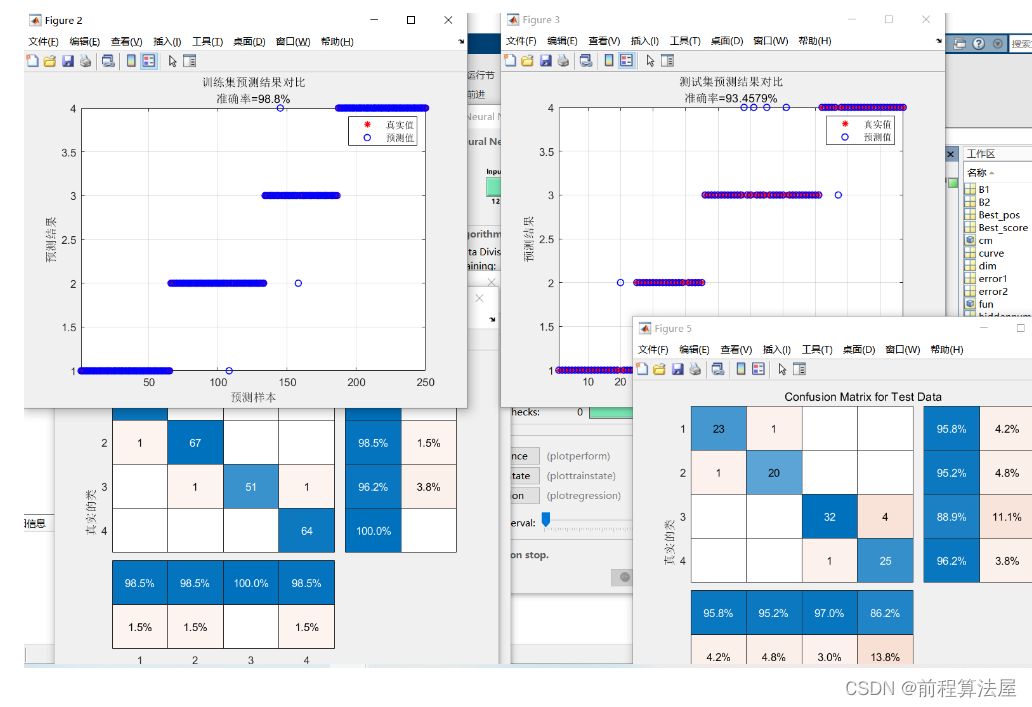
x.1 logistic regression
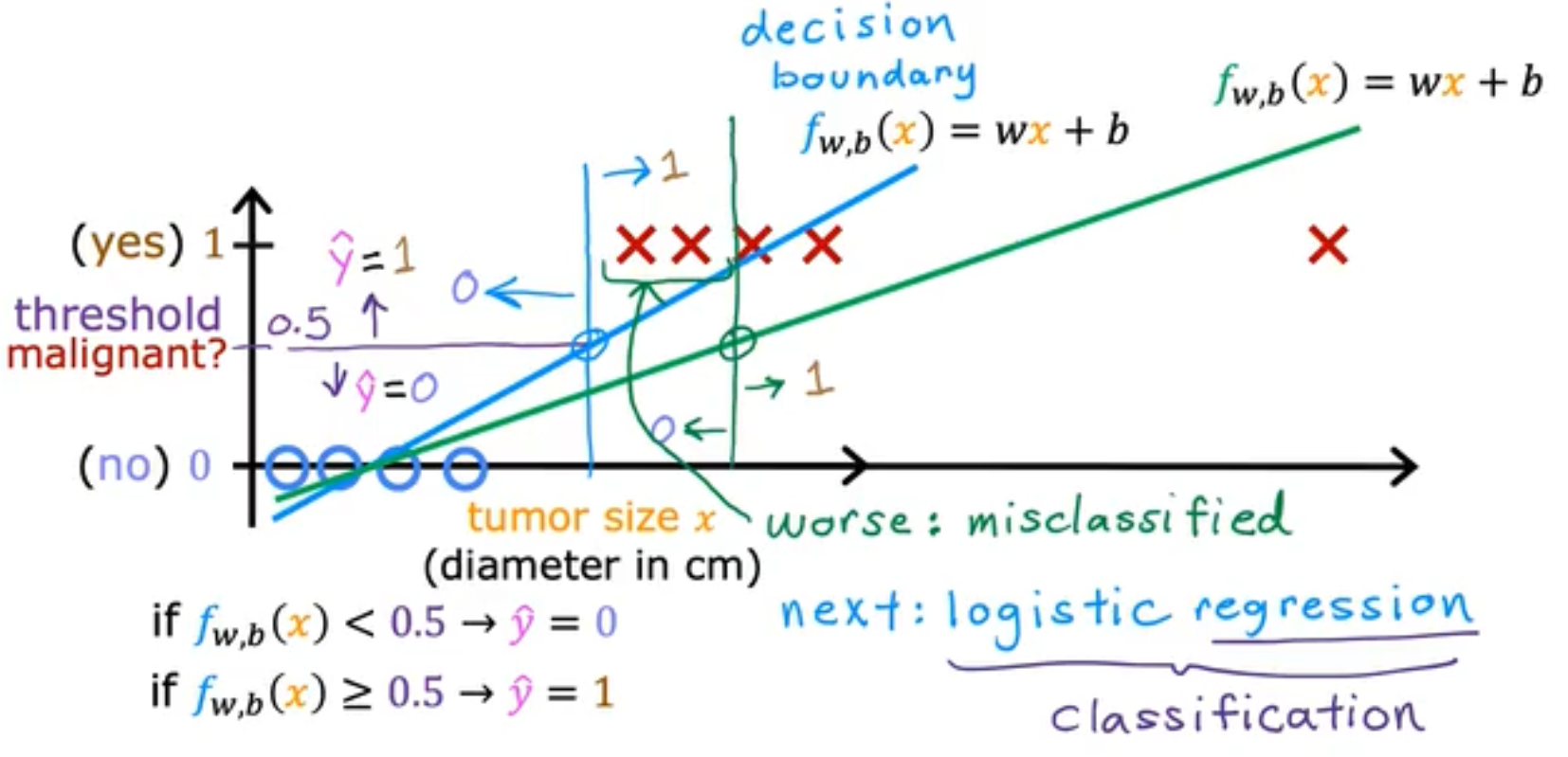
对于诸如分辨细胞是恶性肿瘤细胞与否的类似分类问题,我们使用Linear Regression的模型并不合适,所以引入Logistic Regression的模型,并绘制decision boundary,如下,
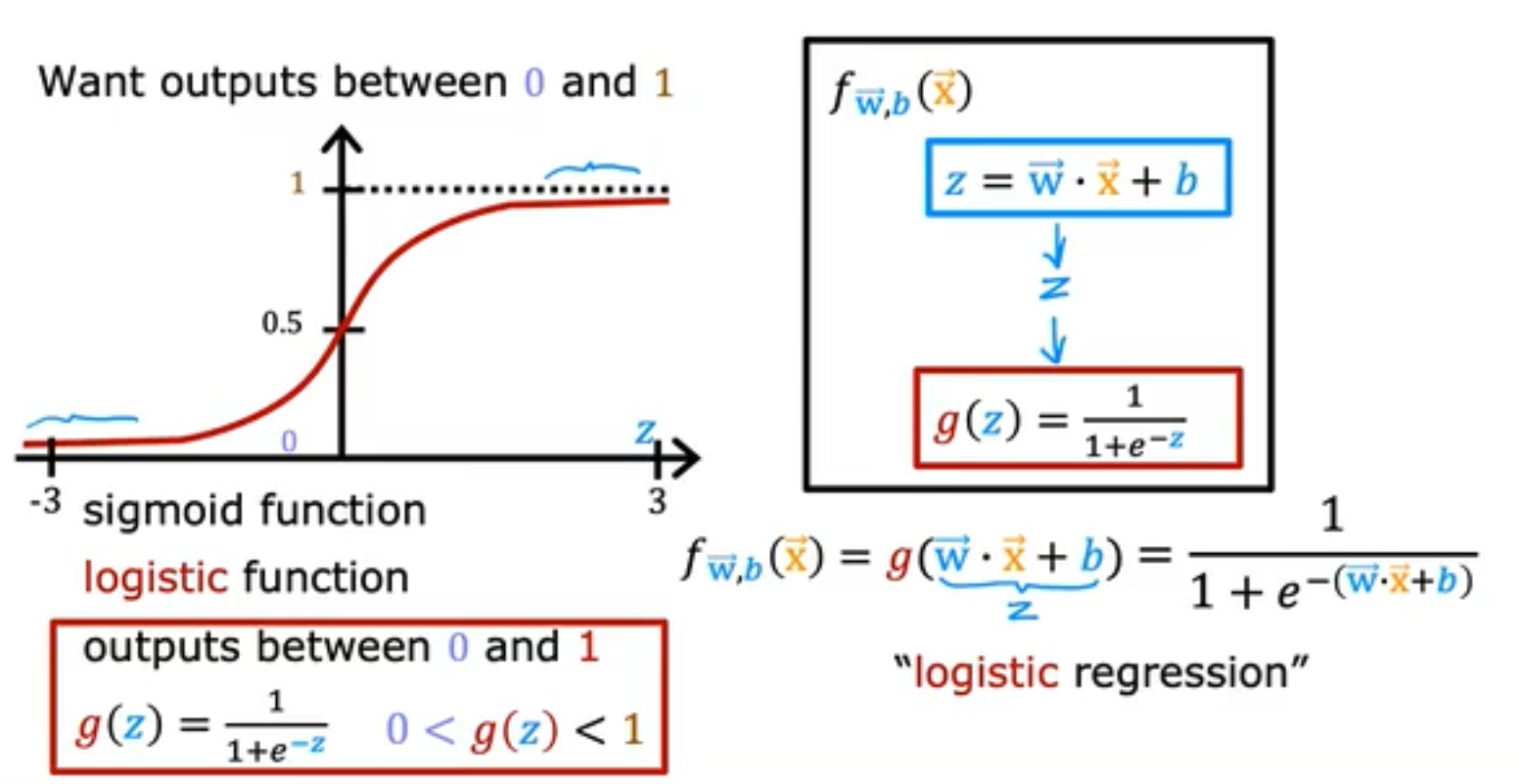
Classification的最后一层,使用sigmoid作为激活函数 g ( z ) = 1 1 + e − z g(z)=\frac{1}{1+e^{-z}} g(z)=1+e−z1,使得最终的输出在[0, 1]这很符合概率分布,
x.2 decision boundary
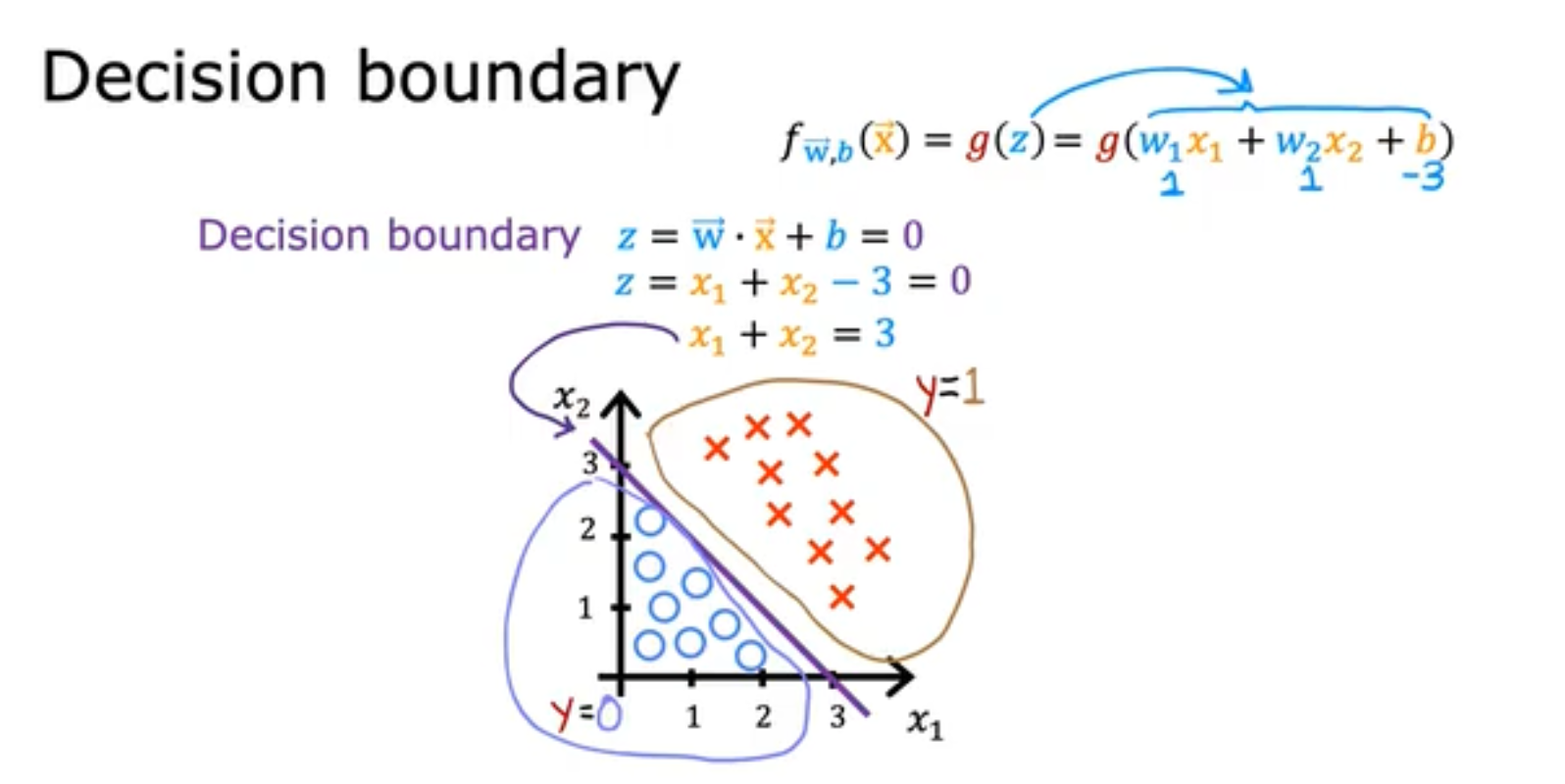
我们使用decision boundary来对数据集的类别进行分类,如下我们便是使用z构造了decision boundary,

x.3 cost function for classification
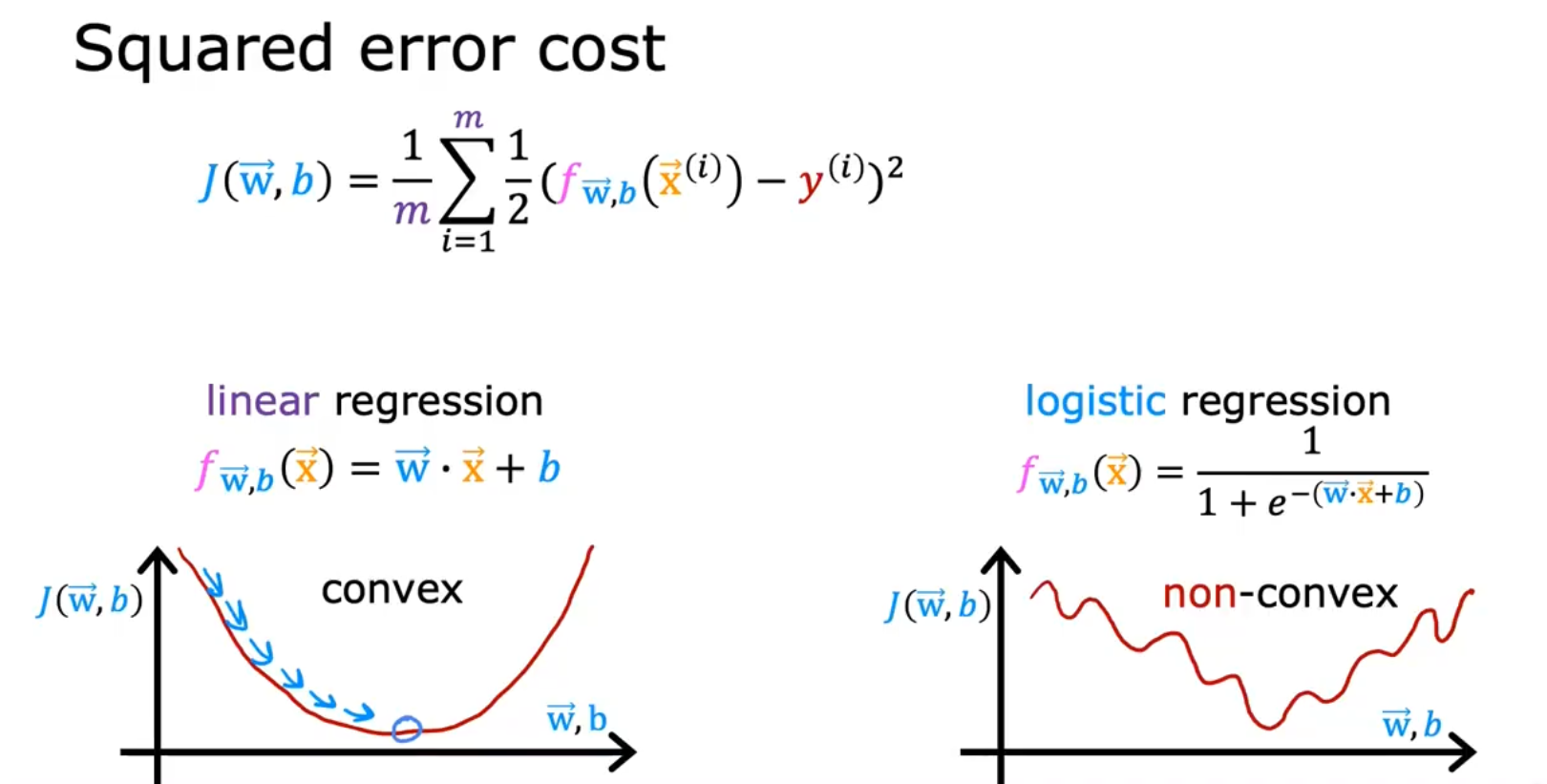
对于分类问题而言,MSE均方差并不是一个很好的策略/损失函数,以肿瘤分类为例子,我们首先构造数据集如下,

如果我们继续使用MSE作为策略/cost function/J(w),那么我们得到的J(w)-w曲线则得到了如右下角的非凸函数,由于存在很多局部最优解(即多个极值),这并不适合收敛,
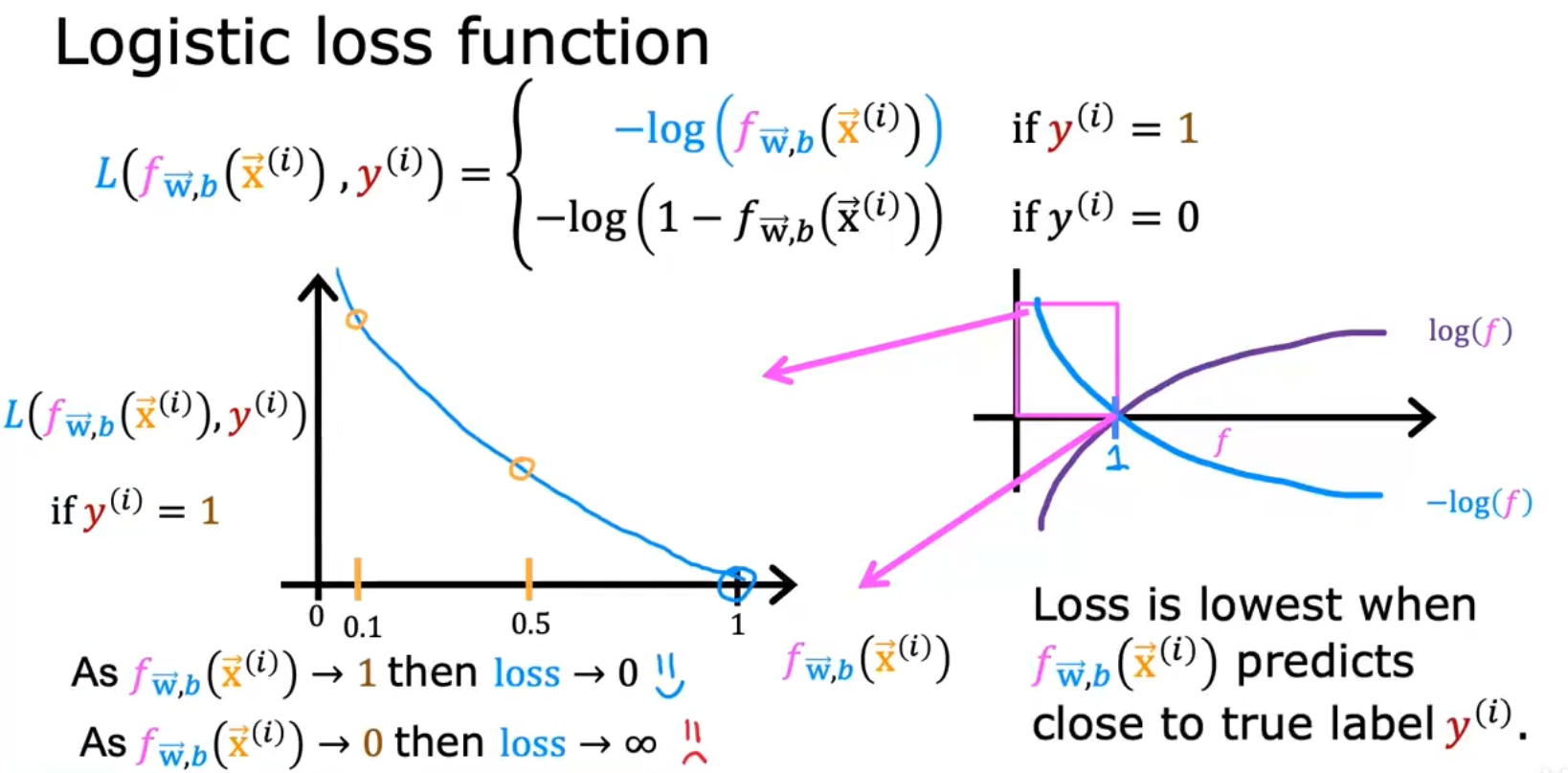
我们引入Logistic loss function使得J(w)-w再次变成convex func凸函数,当y=1时,y_hat属于[0, 1],越远离1,loss越大;当y=0时,y_hat越远离0,loss越大。
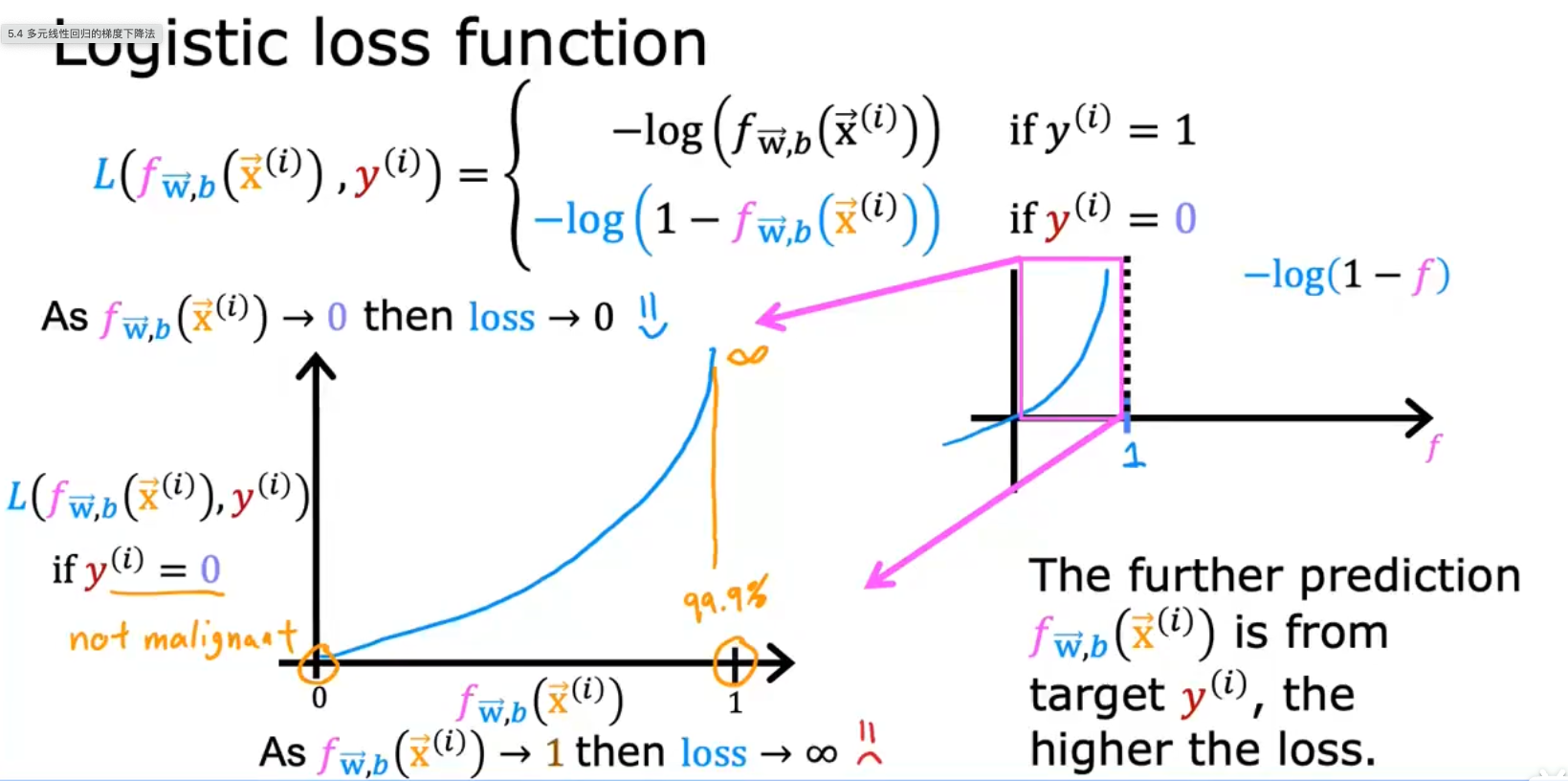
而对于J(w)-w为什么是凸函数的证明,已经超出了本课程的范围,不证明。但是可以在课件中找到,很重要,
但是上面的Loss是一个分段函数,需要两个式子才能组合成上面的loss,我们更希望使用的loss是一个式子,所以我们使用简化表示,将两个式子合并为一个式子,

当然你可能想问,为什么会使用这样的损失函数,其实什么样的模型用什么样的cost func都是使用MLE极大似然估计来估计出来的,背后的数学原理很深,你可能知道怎么推导了,也不知道为什么会这么推,我们这里只需要把loss记住便可。

x.4 将Gradient Descent应用到Classification中
在有了策略函数cost func后,我们可以将Gradient Descent应用到分类模型上,如下,

我们意识到Classification的Gradient Descent中更新参数的方式和Linear Regression是一样的,但是我们也得意识到我们所用模型是完全不同的,同时相同的有向量化加速计算,特征放缩使更容易收敛等知识,